O příspěvku
PDF ke staženíZ jídelního lístku Fyzikální kavárny při ÚFE PŘF MU aneb Kundtova a Rubensova trubice
Nejefektnější demonstrace stojatého vlnění v plynu a možná jedna z nejefektnějších demonstrací ve fyzice vůbec, je stojaté vlnění na Rubensově trubici. Poněkud méně experimentálně náročná, ale také méně efektní, je demonstrace stojatého vlnění pomocí Kundtovy trubice. Kundtova trubice zobrazuje stojaté vlnění „otiskem“ kmitajícího vzduchu do vhodného granulárního materiálu, Rubensova trubice zobrazuje akustický tlak pomocí plamínků hořícího plynu unikajícího z řady malých otvorů podél trubice. V obou případech mohou zvídavější žáci objevit jevy, jejichž interpretace není jednoduchá, a které byly svého času předmětem diskuse známých fyziků v odborných časopisech. S postupem doby se na závěry tehdejší diskuse, zdá se, poněkud zapomnělo a příslušné práce jsou málo citovány. Cílem článku je tuto oblast připomenout a doplnit o některé experimentální zkušenosti autora.
Kundtova trubice
Kundtova trubice nese jméno po německém fyzikovi Augustu Adolph Eduard Eberhar Kundtovi (18.11.1839 - 21.5.1894), který se zabýval akustikou a zejména optikou. V původním provedení se jednalo o akustický rezonátor v podobě skleněné trubice. Na jedné straně byl pohyblivý píst pro ladění, z druhé strany do trubice zasahovala rezonanční tyč vybavená lehkým (korkovým) pístkem. Mezi pístkem a trubicí musela být malá vůle. Trubice se vyplnila přiměřeným množstvím vhodného granulárního materiálu, který se v kmitnách rozviřoval a v uzlech usazoval. (Používala se korková drť popřípadě výtrusy plavuně, tzv. plavuňový prášek plavuň vidlačka- Lycopodium clavatum L).
Jenže v granulárním materiálu byla také pozorována jemná struktura v podobě příčných proužků ve vzájemné vzdálenosti od jednoho mm do několika mm. Tato struktura byla svého času předmětem mnoha diskusí a experimentů. Zvážíme-li, že pro ![]() vychází měřením vzdálenost proužků
vychází měřením vzdálenost proužků ![]() , muselo by se jednat asi o 100 harmonickou s frekvencí
, muselo by se jednat asi o 100 harmonickou s frekvencí ![]() . Je velmi nepravděpodobné, že by všechny harmonické složky měly zanedbatelné amplitudy až na jednu v ultrazvukové oblasti. Ovšem z druhé strany, vzhledem k tomu, že akustické kmity byly generovány podélnými kmity rezonanční tyče o které se nevědělo, jak vlastně kmitá, nebyla tato možnost zcela vyloučena. Experimenty komplikovala skutečnost, že sklo a granulární materiál se vzájemným třením elektricky nabíjí a vzniklý náboj ovlivňuje vzdálenost proužků. Základní otázka zněla, je příčinou jemné struktury vyšší harmonická složka?
. Je velmi nepravděpodobné, že by všechny harmonické složky měly zanedbatelné amplitudy až na jednu v ultrazvukové oblasti. Ovšem z druhé strany, vzhledem k tomu, že akustické kmity byly generovány podélnými kmity rezonanční tyče o které se nevědělo, jak vlastně kmitá, nebyla tato možnost zcela vyloučena. Experimenty komplikovala skutečnost, že sklo a granulární materiál se vzájemným třením elektricky nabíjí a vzniklý náboj ovlivňuje vzdálenost proužků. Základní otázka zněla, je příčinou jemné struktury vyšší harmonická složka?
Přesvědčivé experimenty publikoval E.N. da C. Andrade z University of London [2]. Příčinou tvorby jemných proužků je vznik vírů, které se za určitých podmínek vytvářejí kolem každé částečky od určitého rozměru. Tyto víry se skládají ve vírovou strukturu, která je příčinou seřazení zrníček drti do proužků. Pokud se pokus provede s trubicí, jejíž stěna se nemůže výrazněji elektricky nabíjet, vzdálenost mezi proužky závisí na frekvenci a na vzdálenosti od uzlu stojatého vlnění. Přehled problematiky je podán v [1].
Provedení experimentu:
Rezonátor musí být průhledný. Před plastovou trubkou je lépe dát přednost sklu, které se o něco méně elektricky nabíjí třením s kmitajícím práškem. K buzení akustického signálu je nejjednodušší použít reproduktor. Pro vyšší frekvence stačí malé reproduktorky o průměru je kolem 40 mm s výkonem od 0,5 w. Pokud má reproduktorek stejný průměr jako trubice, je nejjednodušší ho na trubici přímo přilepit, tím se ale komplikuje čištění. Rozebíratelnost se dá zajistit například tak, že reproduktorek přilepíme ke krátké trubici (přibližně) stejného průměru jako je skleněný rezonátor. Mezikus vyrobíme z PET láhve smrštění horkým vzduchem. Podobným způsobem z PET láhve vyrobíme stínící komůrku, která učiní experimenty poněkud snesitelnější. Viz obr.(1)

Obrázek 1
Pro nižší frekvence je zapotřebí basový reproduktor. Vzhledem k jeho většímu průměru potřebuje vhodnou přechodku. Využití kanalizačních tvarovek sice není ideální, ale zato poměrně jednoduché viz obr. 2, 3. Tato varianta dovoluje zasouvat do trubice z jedné strany sondu (mikrofónek) z druhé strany zakončení s různou akustickou impedancí nebo ladící píst.

Obrázek 2
K zobrazení kmiten a uzlů se osvědčila korková drť, nebo jemná jablečná vláknina, kterou rozmístíme v potřebném množství rovnoměrně podél trubice. V případě projekce zpětným projektorem nesmí drť vytvořit souvislou vrstvu.
Pokud je ladění na generátoru příliš hrubé, je lépe vybavit trubici na uzavřeném konci pohyblivým pístem. Při nižších frekvencích, lze experiment provést jak s uzavřeným, tak s otevřeným koncem.
Má-li skleněná trubice vnější průměr kolem 40 mm a větší a tlouštku stěny kolem 2,5 mm a menší, lze strukturu poměrně dobře promítat klasickým zpětným projektorem, viz obr. 3. Problém s malým zorným polem lze částečně obejít posouváním meotaru podél trubice.

Obrázek 3
Rychlost kmitání vzduchu na ose uzavřené trubice délky L buzené kmitajícím pístem s rychlostí kmitání
![]()
je popsáno vztahem (osa trubice je ztotožněna s osou x, pozice kmitajícího pístu ![]() , souřadnice konce trubice
, souřadnice konce trubice ![]() )
)
![]()
akustický tlak
![]() ,
,
kde ![]() a rezonanční podmínka je
a rezonanční podmínka je
![]() .
.
Poznámka č. 1.
Rychlost zvuku při teplotě ![]() a vlhkosti
a vlhkosti ![]() je
je ![]()
Poznámka č. 2.
Rezonanční podmínka (4) platí v případě, kdy je splněna okrajová podmínka (1) (kmitající píst v trubici) a odrazivost ucpávky je ![]() .
.
Rezonanční podmínka (4) platí také pro otevřenou trubici (![]() ), pro budící signál (okrajová podmínka)
), pro budící signál (okrajová podmínka) ![]() , kde
, kde![]() je tlak.
je tlak.
Pokud je reproduktor napojen na trubici způsobem podle obr. 2 a obr. 3, okrajová podmínka (1) neplatí.
Experiment:
Se zařízením dle obr. 2, resp. obr. 3. Šířka proužků při rezonanci, měřeno v blízkosti kmitny rychlosti, spolu se změřenou rezonanční frekvencí je v tabulce (1).
| č. |
rezonanční frekvence Hz (δ = 1 %) |
vzdálenost proužků mm (δ =10 %) |
| 0 |
83 |
25 |
| 1 |
195 |
7 |
| 2 |
330 |
4,1 |
| 3 |
444 |
3,8 |
| 4 |
572 |
2,9 |
Tabulka 1
Poznámka: struktura byla poměrně nepravidelná a vzdálenost proužků vykazovala časový vývoj, pravděpodobně vlivem elektrického náboje.
Struktura proužků v kmitně rychlosti pro amplitudu, kdy jsou proužky nejostřejší (malá amplituda) je na obr. 4, pro amplitudu, kdy je ještě struktura proužků patrná, na obr. 5. Zaznamenáno v trubici s otevřeným koncem při rezonanční frekvenci 135 Hz.

Obrázek 4

Obrázek 5
Při nízké amplitudě se struktura jako by zdvojí, mezi dva proužky se umístí třetí, to je místo, kde ve struktuře vírů (podle [2]) směřuje proudění ke stěně trubice.
Odečtení vlnové délky
Amplituda rychlosti se v okolí maxima mění jen málo. Proto je stanovení polohy kmitny poněkud neurčité. Příliš nepomáhá ani zaostřování polohy postupným zeslabováním budícího signálu s cílem omezit pohyb zrníček na co nejmenší okolí maxima. Uzel je sice teoreticky ostřejší, ale zase se do granulární struktury nezobrazí, protože rychlost kmitání v jeho okolí nestačí k přemisťování drti. Obvyklá struktura korkové drti blízko uzlu (na levo) a kmitny (na pravo) je na obrázku č. 6.
![]()
Obrázek 6
Je patrné, že čím jsou proužky blíž k uzlu (rychlosti), tím jsou blíž k sobě. Pro přesná měření je nejvhodnějším detektorem elektretový mikrofonek.
Zobrazení kmiten a uzlů pomocí žhaveného drátu.
Na obr. 8 je pohled na pomůcku pro zobrazení rychlostního pole kmitajícího vzduchu pomocí žhaveného drátu.

Obrázek 8
Termokantalový drát o průměru 0,1 mm a délky 90 cm je zavěšen na pomocném nosníku na ramíncích z pružinového drátu o průměru 0,3 mm. Zařízení připomíná smyčec. Závěs musí odpružit teplotní dilataci asi 15 mm. Žhavený drát je v místě intenzivního kmitavého pohybu vzduchu více ochlazován. Doladěním žhavení lze dosáhnout kontrastu ve svítivosti drátu mezi místy s maximální a minimální rychlostí proudění. Na obr. 9 jsou zobrazeny stojaté kmity vzduchu v trubici s otevřeným koncem, žhavený drát lícuje na pravé straně s koncem trubice (světlá tečka úplně vpravo). Délka drátu je 90 cm, rezonanční frekvence 520 Hz, změřená vlnová délka 72 cm. Při porovnání frekvence, vlnové délky a rychlosti zvuku je třeba vzít v úvahu značný ohřev vzduchu od žhaveného drátku. (Například při teplotě 100 0C je rychlost zvuku 421 m×s-1.)
![]()
Obrázek 9
Rubensova trubice
Nese jméno po německém fyzikovi Heinrichu Rubensovi (1865-1922), který se zabýval především vzdáleným infračerveným zářením a studiem odrazivosti různých materiálů.
Rubensova trubice představuje vtipné a poměrně jednoduché řešení problému, jak demonstračně zobrazit nikoliv akustickou výchylku, ale akustický tlak stojatého vlnění. Jedná se vlastně o lineární plynový hořák tvořený tenkostěnnou, zpravidla kovovou trubkou o průměru kolem 4 cm s řadou malých otvorů (průměru 0,5 mm až 1,5 mm) vyvrtaných v plášti v pravidelných rozestupech asi 1 cm podél trubice. Na jedné straně trubice je laditelný zdroj vlnění, druhý konec je uzavřen. Do trubice přivádíme pod velmi malým tlakem plyn, které dává svítivý plamen, například propan butan. Naladíme-li zdroj na rezonanční frekvenci, původně stejně vysoké plamínky změní v pravidelných úsecích svoji výšku.
Problém s interpretací spočívá v tom, že někteří experimentátoři naleznou maxima plamínků v místě uzlů akustického tlaku, jiní v kmitnách. Při určitém rozměru otvorů a dalších parametrů lze efektu reverzace maxim a minim dosáhnout s tím stejným experimentálním zařízením. Viz. obr. 10 a obr.11.

Obrázek 10

Obrázek 11
Jediný rozdíl v situaci podle obr. 10 a obr 11. spočívá v jiném nastavení přítoku plynu a amplitudy budícího signálu. Průměr trubice je 50 mm, tloušťka stěny 1 mm. Otvory o průměru 1,5 mm jsou vrtány po jednom cm v délce 101 cm, zdroj zvuku je na levé straně, pevný konec na pravé straně. (Poznámka: v případě porovnávání vlnových délek je třeba vzít v úvahu, že plyn v trubicích nemá stejnou teplotu.)
Problematikou se zabývá například [4], [5].
Ficken a Stephenson [5] odvodili vztah pro hmotnostní průtok plynu ![]() , o hustotě ρ a otvorem o obsahu průřezu A:
, o hustotě ρ a otvorem o obsahu průřezu A:
![]() .
.
kde ![]() je tlak, pod kterým je plyn přiváděn do trubice,
je tlak, pod kterým je plyn přiváděn do trubice, ![]() akustický tlak.
akustický tlak.
Poznámka: tento vztah dostaneme z Bernoulliovy rovnice pro ideální plyn, zanedbáme-li inerční efekty, tj. pro limitu ![]() .
.
Uvažujme případ, kdy
![]() .
.
Výraz (5) pro ![]() můžeme rozvinout v řadu podle
můžeme rozvinout v řadu podle ![]() . Ponecháme lineární a kvadratický člen a spočítáme střední hodnotu. Obdržíme:
. Ponecháme lineární a kvadratický člen a spočítáme střední hodnotu. Obdržíme:
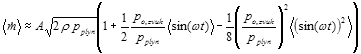 ,
,
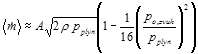 .
.
Vzhledem k tomu, že výška plamínku je nějak úměrná střední hodnotě hmotnostního průtoku plynu, je z rovnice (8) vidět, že v kmitně akustického tlaku bude plamínek nižší než v uzlu. Maxima plamínků odpovídají uzlu akustického tlaku, případ podle obr 10.
Pro případ, že tlak připouštěného plynu je v daném místě zanedbatelný proti akustickému tlaku, je plyn vypuzován jen v části periody (ve zbývající části periody je naopak přisáván vzduch). Střední hodnota hmotnostního průtoku v tom místě je však vyšší, než v uzlu, protože tam je hmotnostní průtok dán je tlakem připouštěného plynu, který je zanedbatelný. Maximum plamínků je v tedy v kmitně akustického tlaku.
Poznámky k experimentu.
Podmínkou stejných plamínků jsou přesně stejné otvory bez grótů. Trubice nemusí být nutně kovová. Funguje i varianta z polypropylénové kanalizační tvarovky. Část trubice, kde jsou vrtány otvory, polepíme hliníkovým samolepícím proužkem. Trubici omotáme místo vedle místa s výjimkou otvorů knotem nebo motouzem, viz obr. 12. Takto upravená trubice po namočení knotu (motouzu) funguje stejně dobře jako kovová, pouze se teplem mírně prohne. Knot nebo motouz stačí odpařováním vody trubici uchladit, musí být ovšem mokrý. To znamená, že trubici je třeba pravidelně vlhčit, nejlépe malou střičkou nebo houbičkou. Na obr. 12 jsou dobře patrné následky opomenutí dovlhčit motouz během experimentu. Kromě částečně ohořelého motouzu však samotná trubice nedoznala žádnou újmu.

Obrázek 12
Bezpečnostní poznámky:
1. Propan butan je těžší než vzduch, může se „rozlít“ po stole nebo natéct do dutin.
2. Nelze vyloučit, že za určitých okolností vznikne v trubici výbušná směs propan butanu se vzduchem. Prošlehnutí plamene do trubice by pak mělo za následek vystřelení reproduktoru a ucpávky. Okolí v blízkosti osy trubice je proto třeba považovat za potenciálně nebezpečný prostor.
Literatura
[1] Robert A.Carman: Kundt Tube Dust Striations. In:Am. J. Phys. 23, 505 (1955)
[2] E.N. da C. Andrade, Trans. Roy. Soc. (London) A 230, 413 (1932)
[3] Halliday D. a kol.: Fyzika. VUTIM Brno, Prometheus Praha, 2000.
[4] George F. Spagna, Jr.: Rubens flame tube demonstration: A closer look at the flame. In:Am. J. Phys.51, 848 (1983).
[5] G. Ficken and F.C. Stephenson, Phys. Teach. 17, 306 (1979).