Led – přítel fyzika
Abstrakt
Voda je asi nejfantastičtějším materiálem ve vesmíru a její pevné skupenství ji v tomto nedělá ostudu. Příspěvek je zaměřen na zkoumání základních vlastností ledu jak ve formě demonstračních experimentů tak také domácích experimentálních úloh.
Anomálie vody
Voda je látkou, se kterou se běžně stýkáme a proto nás většinou ani nenapadne, jak moc je výjimečná. Dovolím si zde uvést alespoň několik vlastností, kterými se výrazně liší od chemicky srovnatelných látek (podle [1], kde naleznete i dalších 37 odlišností a také jejich vysvětlení): vysoký bod tání, vysoký bod varu, velké povrchové napětí, velká viskozita (která navíc s rostoucím tlakem klesá), při tání zvětšuje svou hustotu, v rozmezí 0°C až 4°C její hustota s rostoucí teplotou vzrůstá, může být podchlazena až na –70°C (v malých kapkách).
Změny objemu při tání a tuhnutí
Voda při tuhnutí na rozdíl od ostatních běžných látek zvětšuje svůj objem. Nejjednodušší demonstrací tohoto faktu je zamrzlá PET láhev. Stačí naplnit libovolnou PET láhev vodou, zašroubovat a vložit na 24 hodin do mrazáku. Tuhnoucí voda láhev silně zdeformuje (při pokusech s tlakováním PET láhve vzduchem dochází k podobným deformacím až při tlacích nad 300 kPa). Pokud necháte zamrznout vodu v Tetrapakové krabici se šroubovacím uzávěrem, tak ji led roztrhne. V žádném případě nesmíte tyto pokusy provádět se skleněnou láhví! Čistit mrazák od skleněných střepů není příjemnou prací.
Jako domácí úlohu lze žákům zadat změření změny objemu vody při tuhnutí. Osvědčila se 20 ml injekční stříkačka, do které natáhneme 15 ml vody a vložíme do mrazáku (výstup pro nasazení jehly není nutno zatěsňovat). Stříkačka je z houževnatého plastu, takže ji led neroztáhne, zato ale posune píst stříkačky až ke značce 16 ml. To odpovídá nárůstu objemu o 1/15 = 7% (přesnější hodnota je 8,3%).
Žáci většinou tuto vlastnost vody znají, netuší ale, že ostatní materiály se chovají opačně. Vhodnou demonstrací je použití vosku. Roztavíme vosk v zavařovací sklenici ponořené ve vařící vodě a nalijeme ho do zkumavky. Během tuhnutí se povrch vosku výrazně propadne dolů – jeho objem poklesl.
Podobně lze předvést plování látky na vlastní tavenině – do jedné skleničky nalijeme vodu a vhodíme kousek ledu – plove na hladině (to je ale vcelku známý fakt). Do další skleničky nalijeme roztavený bílý vosk a vhodíme dovnitř kousek pevného barevného vosku – klesne ke dnu.
Regelace ledu
Regelace ledu bývá ve staré literatuře (např. [2]) označována jako „slévání se“. Jedná se o opětovné přimrznutí dvou oddělených kusů ledu. Velmi pěkný pokus popsaný ve [2] provedeme následovně: vezmeme dva větší kusy ledu (nebo rozbijeme jeden velký) a vhodíme je do nádoby s horkou vodou (ne vařící, budeme do ní namáčet ruce). Chytneme oba kusy ledu a v horké vodě je přitiskneme na chvíli k sobě – spojí se natolik pevně, že jeden zůstane viset na druhém.
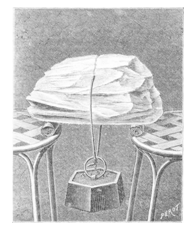
Vysvětlení tohoto na první pohled překvapivého jevu je prosté – led, který neroztál, má teplotu stále pod bodem tuhnutí. Když k sobě přitiskneme dva kusy ledu, tak vrstvička vody, která mezi nimi zůstala, není obklopena horkou vodou, ale chladným ledem – zmrzne. Oba kusy ledu přimrznou k sobě.
Snad každý učitel fyziky si při zaslechnutí slova „regelace“ vybaví klasický pokus, kdy se tenký drát na koncích zatížený pomalu zařezává do bloku ledu a přitom se led v místech, kde struna prošla, opět spojí. Obrázek, kterým tento pokus ilustruji, převzal [2] z francouzského časopisu „La Nature“.
Moderní verzi téhož můžeme provést tak, že konce tenké ocelové struny (lze koupit v obchodech s modelářskými potřebami) uchytíme do vršků od PET lahví a vršky přišroubujeme na dvoulitrové PET lahve naplněné vodou.
U tohoto pokusu se ustálilo vysvětlení, že při zvýšeném tlaku klesá bod tání ledu, pod drátem tedy led roztaje a za drátem se opět slije, neboť se tlak vrací na původní hodnotu. A že podobný efekt funguje i u bruslí (proto musí být zabroušené do hrany). V kuloárech několika předchozích Veletrhů se však probírala myšlenka, že je to třeba všechno trochu jinak. Jedním z nápadů, který zde zazněl, byl vliv tepelné vodivosti ocelového drátu. Pokusil jsem se to ověřit. Jelikož k pokusu používám ocelovou strunu o průměru 0,2mm, zašel jsem do obchodu s rybářskými potřebami a koupil si lanko Dynastrong o stejném průměru (je to pletené rybářské lanko z vlákna Dynema, které je vyráběno z GSP = Gel Spun Polyethylene = vlákno předené z gelové formy polyetylénu).
Na jeden blok ledu jsem zavěsil jak strunu tak lanko a zatížil je shodnou zátěží – vyvíjely stejný tlak. Ocel pomalu ale jistě procházela ledem zatímco lanko se sice trochu zařezalo (asi 4 cm pod povrch), tam se ale jeho postup zastavil a lanko zamrzlo. Polyetylén je ve srovnání s ocelí tepelný izolant, takže tím jsem měl problém za vyřešený. Pak mě ale napadlo vyzkoušet pokus za nízké venkovní teploty. V dubnu jsem měl k dispozici pouze prostor ledničky s +4°C. Zde by už mělo být ohřívání struny okolním vzduchem silně potlačeno, ale struna se přesto do ledu zařezala.
Shodou okolností se mi po měsíci dostal do rukou několik čísel časopisu The Physics Teacher (díky Doc. Trnovi z PedF MU v Brně, který mi jejich zapůjčení zprostředkoval), kde jsem nalezl článek [3], zabývající se stejnou problematikou.
Zde je uvedeno, že k poklesu bodu tání vody o 1°C je nutno vyvinout tlak 14 MPa, přičemž podle výpočtu pod strunou vzniká tlak pouze 2 MPa, což by zajistilo pokles teploty tání o pouhou desetinu °C. V článku [3] je jev vysvětlován pomocí tzv. „povrchového tání“, jehož existenci předpověděl už v roce 1842 Michael Faraday. Podle této hypotézy existuje na povrchu pevných látek tenká vrstva kapaliny i při teplotách pod bodem tání (snižuje to její tzv. volnou energii povrchu). U ledu se jedná o vrstvičku o tloušťce 40 nm při teplotě 0°C a o tloušťce 0,5 nm při teplotě ‑35°C. Tato vrstvička je příčinou průchodu struny ledem i snadného bruslení na ledové ploše při teplotách těsně pod bodem mrazu. Podle autora článku [3] však na ledě o teplotě ‑35°C prakticky bruslit nelze – má příliš tenkou povrchovou vrstvu kapalné vody – brusle nekloužou. Vyzkoušel si to prý osobně při arktické zimě v Kanadě.
To, že výše uvedená hypotéza je akceptovatelným vysvětlením experimentu, potvrdily i experimenty R.R.Gilpina, který pokus v roce 1980 opakoval s použitím velmi malých sil působících na strunu (tzn. snížení bodu tání bylo možno zanedbat) a při teplotě pokusné aparatury udržované pod 0°C. I při těchto podmínkách struna procházela ledem.
Zamrzání nádoby s vodou
Předloni jsem v zimě položil za okno pouťový balónek naplněný vodou a čekal jsem, že ráno budu mít k dispozici ledovou kouli. K mému překvapení však i přes velký mráz zamrzla pouze relativně tenká vrstva vody na okraji a vnitřek zůstal kapalný – vzniklo ledové vejce.Takovéto vejce si můžete vyrobit sami, pokud dáte balónek naplněný vodou do mrazáku na 5-6 hodin.
Jak je možné, že voda uvnitř vejce odolává zmrznutí? Musíme si uvědomit, jaké procesy probíhají při zamrzání. Voda se nejprve ochlazuje k bodu tání (či mírně pod něj) a teprve potom zamrzá. Jak při ochlazování tak při zamrzání musí odevzdat velké množství tepla okolí. Ze začátku je okolím mrazivý vzduch mrazáku, takže voda v balónku se relativně rychle ochladí na 0°C (balónek je ochlazován ze všech stran, samovolné proudění vody o různé teplotě – konvekce – zajistí stejnou teplotu uvnitř celého objemu).
Na okraji balónku se vytvoří tenká vrstva ledu. Voda uvnitř už může teplo odevzdávat pouze ledové slupce, která má ale teplotu srovnatelnou s vodou – předávání tepla se téměř zastaví. Aby došlo k namrznutí další vrstvy vody, musí se předat velké množství tepla skrze vrstvu ledu, který není dobrý vodič. Navíc se led musí nejprve ochladit pod bod tání, aby byl schopen vodě teplo odebírat. Vznikem byť i tenké vrstvičky ledu se proces zamrzání prudce zpomalí. Voda uvnitř ledového vejce přechází do podchlazeného stavu – má teplotu nižší než je bod tání, ale přesto nezamrzne. Pro přechod do tohoto stavu stačí odevzdat mnohem menší teplo než pro zamrznutí.

Uvnitř ledového vejce už nedochází k „běžnému“ zamrzání, ale k zamrzání podchlazené vody. Když takové vejce rozbijete, možná objevíte podivné ploché keříčkovité útvary, které se vzájemně kříží a prorůstají. Na obrázku vpravo, který byl převzat ze [4], můžete vidět jeden z těchto (tzv.Tyndallových) útvarů.
Když necháte ledové vejce v mrazáku několik dní a teprve poté ho rozbijete, zjistíte, že po okraji je cca centimetrová vrstva čirého ledu (vzniklého „běžným“ zamrzáním) a vnitřek je vyplněn bílou houbovitou strukturou, která obsahuje velké množství nezamrzlé vody. Tato houba vznikla prorůstáním plochých keříčkovitých útvarů. Dobrou „líhní“ takovýchto útvarů vhodných k pozorování je hlubší miska z pěněného polystyrenu (prodává se na nich ovoce, zákusky, maso, ...). Naplníme ji alespoň do 4cm vodou a vložíme do mrazáku. Díky izolačním vlastnostem plastu voda zamrzá odshora a podobně jako u balónku zde nejprve vznikne vrstva čirého ledu a postupně se uvnitř podchlazené vody začnou vytvářet keříčkovité (dendritické) útvary (po cca 4 hodinách v mrazáku). Máte-li štěstí, získáte keříčky o ploše deseti či více centimetrů čtverečních.
Polarizační vlastnosti ledových krystalů
Když vložíme destičku ledu (například ze zamrzlé hladiny vody v misce) mezi dva zkřížené polarizační filtry, zjistíme, že krystaly ledu stáčejí polarizační rovinu světla. Objeví se krásný obraz mnoha malých krystalků ledu – některé jsou černé, jiné světlé. Velmi tenké krystaly dokonce vytvářejí barevné plošky. Pokud se podaří na plochu umístit keříček vzniklý v podchlazené vodě, má celý jednu barvu – je tvořen monokrystalem.
Poznámka
Popis experimentu demonstrujícího existenci a velikost měrného skupenského tepla tání ledu naleznete na adrese [5].
Článek „Zkoumání teplotní anomálie vody“ věnovaný anomálnímu průběhu hustoty vody vyjde v nejbližší době v časopise Matematika-fyzika-informatika.
Literatura
[1] http://www.lsbu.ac.uk/water [cit 2005-08-21]
[2] Fyzika bez přístrojův. Vesmír, říjen 1881
[3] White J.D.: The Role of Surface Melting in Ice Skating. The Physics Teacher, Vol.30, Nov.1992, s. 495-497
[4] Walker J,: Exotic Patterns Appear in Water When It Is Freezing or Melting. The Scientific American, July 1986
[5] http://fyzweb.cuni.cz/piskac/pokusy/www/energie/tanidrcl.htm [cit 2005-08-22]