O příspěvku
PDF ke staženíPokusy s kyvadly
Vliv silového pole na frekvenci kyvadla
1. varianta
Potřeby: Fyzické kyvadlo s dvoustranným hrotovým závěsem, opatřené vespod feritovým magnetem, řada souhlasně orientovaných spojených magnetů délky 0,25 m, stativ (obr. č. 1).
Provedení: Kyvadlo rozkmitáme a pozorujeme jeho frekvenci v gravitačním poli. Pak pod něj (3–4 cm) umístíme řadu magnetů tak, aby její orientace souhlasila s orientací magnetu kyvadla. To bude kmitat s vyšší frekvencí než původní, při obrácení řady se frekvence sníží. Značného snížení frekvence dosáhneme přiblížením řady na několik mm, při opačné orientaci nebude kyvadlo kmitat.
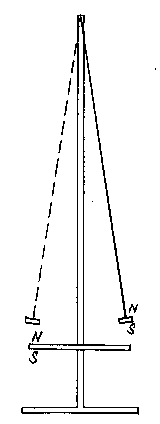
Obr. 1
Vysvětlení: Účinek gravitačního pole na kyvadlo můžeme posílit nebo zeslabit přítomností magnetického pole. Výsledný silový účinek obou polí je buď větší nebo menší a v posledním případě má orientaci vzhůru. Proto kyvadlo nebude kmitat a zůstane vychýleno na kraji magnetického pole.
Poznámka: Magnetické pole řady není homogenní a magnetické pole kyvadla se během kmitu natáčí. Proto kmity kyvadla nejsou přesně harmonické.
2. varianta
Potřeby: Těleso o hmotnosti 0,75 kg s dlouhým vláknovým závěsem, na tělese připevněný model krátkého matematického kyvadla s hmotností 7,5 g, stativ výšky 2 m opatřený kladkami, aretací a třecí brzdou (obr. č. 2).
Provedení: Těleso zvedneme do nejvyšší polohy a zaaretujeme. Rozkmitáme kyvadlo a po několika vteřinách uvolníme soustavy tělesa s kyvadlem do volného pádu. Během pádu nebude kyvadlo kmitat.
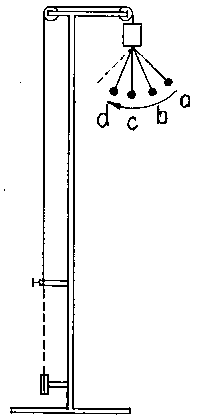
Obr. 2
Vysvětlení: Při volném pádu je silový účinek gravitačního pole na kyvadlo v rámci soustavy nulový a to během pádu nekmitá. Při provedení hraje roli poloha kyvadla v okamžiku uvolnění soustavy k pádu (obr. č. 2). V poloze a je uvolněna při amplitudě kyvadla, jeho kinetická energie je nulová, potenciální se v rámci soustavy neuvolňuje a vzájemná poloha tělesa a kyvadla se během pádu nemění. V polohách b–d má kyvadlo jistou kinetickou energii, která není při pádu blokována. Na počátku pádu je využita částečně k ovlivnění směru pohybu a rychlosti tělesa (proto je vhodné, aby těleso mělo mnohonásobně větší hmotnost než kyvadlo), částečně k dosažení jisté výchylky kyvadla. V tomto okamžiku se přestane kyvadlo v rámci soustavy pohybovat. Po zabrždění pádu se opět rozkmitá.
Parametrická resonance
1. varianta
Potřeby: Model matematického kyvadla, stativ opatřený kladkami (obr. č. 3).
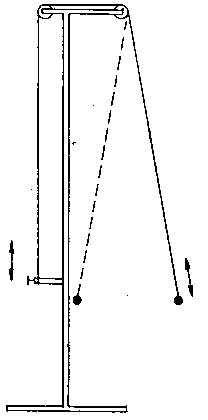
Obr. 3
Provedení: Kyvadlo rozkmitáme s malou amplitudou. Změnami délky kyvadla vyvoláme resonanci, která se projeví růstem amplitudy.
Vysvětlení: Pro vznik parametrické resonance je nutné splnit následující podmínky:
a) Kyvadlo (resonátor) musí být předem uvedeno do kmitavého pohybu.
b) Změny parametru (délky) kyvadla musí mít dvojnásobnou frekvenci než kyvadlo.
c) Průběh kmitů kyvadla a změn jeho délky musí mít příslušný fázový posun, odpovídající i těsnosti vazby.
Pokud nejsou všechny uvedené podmínky splněny, k resonanci nedojde.
2. varianta
Potřeby: Pružina s tuhostí 20 N∙m-1, závaží 0,1 a 0,2 kg, vláknový závěs délky 0,13 m, stativ (obr. č. 4).
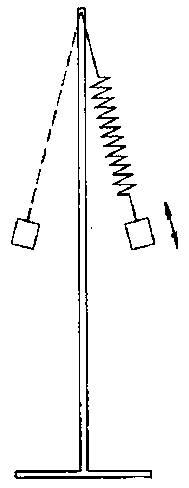
Obr. 4
Vysvětlení: Ke zvyšování amplitudy fyzického kyvadla je využívána energie kyvadla pružinového a naopak.
Provedení: Pružinu zatížíme závažím 0,1 kg. Toto kyvadlo může kmitat jako pružinové i fyzické. Pak jej rozkmitáme v souladu s podmínkami resonance a amplituda fyzického kyvadla vzrůstá. Vlivem ne zcela přesného nastavení poměru frekvencí 2:1 dojde ke změně časového průběhu fyzického a pružinového kyvadla, vymění se role oscilátoru a resonátoru a vzrůstá amplituda kyvadla pružinového. Při použití závaží 0,2 kg a prodloužení kyvadla o 0,13 m resonance probíhá při nižších frekvencích.
Poznámka: Uvedené číselné hodnoty jsou pouze informativní, k dané pružině je nutno je doladit.
3. varianta
Potřeby: Fyzické kyvadlo s možností časově řízených změn jeho redukované délky, feritový magnet vyznačující nulovou polohu kyvadla, stativ (obr. č. 5).
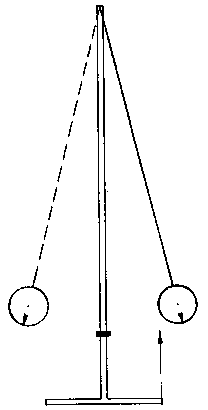
Obr. 5
Provedení: Kyvadlo rozkmitáme a pozorujeme zvyšování amplitudy kmitů.
Vysvětlení: Změny délky uvnitř kyvadla jsou zajištěny elektromagnetem včetně elektrického zdroje a časově řízeny vzhledem k jeho nulové poloze.
Pohyb vzduchové bubliny v kapalném prostředí.
Potřeby: Vysoký odměrný válec, injekční stříkačka, trubička (Ø 2 mm), spojovací hadička, průhledná kapalina s vyšší viskozitou (obr. č. 6).
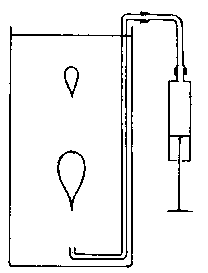
Obr. 6
Provedení: Tlakem ve stříkačce vytvoříme u dna válce vzduchovou bublinu o Ø 1–1,5 cm. Ta stoupá vzhůru téměř konstantní rychlostí, přičemž se deformuje do kapkovitého tvaru.
Nejprve vytvoříme bublinu menšího objemu a když vystoupí do poloviny výšky válce, vytvoříme bublinu s větším objemem. Ta stoupá vyšší rychlostí a první dohání.
Vysvětlení: Bublina představuje málo hmotné těleso s nízkou hustotou, které je snadno tvarově deformovatelné. Pokud by se v kapalině nepohybovala, měla by vlivem povrchového napětí kapaliny kulový tvar. Při dostatečné rychlosti pohybu s laminárním obtékáním je nestejným tlakem v různých místech povrchu deformována do kapkovitého tvaru.
Na rychlost bubliny mají rozhodující vliv vztlaková síla, která je přímo úměrná jejímu objemu, tedy třetí mocnině rozměru, a odpor prostředí, který je závislý na čelním průřezu, tedy na druhé mocnině rozměru. Tato rozdílná závislost způsobuje, že větší bublina stoupá rychleji.
Poznámky: Pokud má bublina velice malý objem, nebo kapalina vysokou viskozitu (med), stoupá bublina tak pomalu, že se nedeformuje zřetelně do kapkovitého tvaru.
V prostředí s nízkou viskozitou (voda) stoupá větší bublina tak rychle, že je obtékána turbulentně, mění svůj tvar během pohybu, což vyvolává průběžné zakřivování její dráhy.
Vlivem většího hydrostatického tlaku u dna má bublina zpočátku nejmenší objem a tedy i nejmenší rychlost, pod hladinou stoupá naopak nejrychleji.