O příspěvku
PDF ke staženíFyzik cyklista
Abstrakt
Jízdní kolo spojuje mnoho technických řešení. Všechna využívají základní zákonitosti fyziky, proto je kolo vhodnou učební pomůckou ve výuce na základní škole. Důležitá je také technika jízdy, šlapání do pedálů, rozložení hmotnosti, aerodynamický tvar. Jízdní kolo tak můžeme použít jako spojovací článek při tvorbě mezipředmětových vztahů mezi fyzikou, technickou výchovou, informatikou, tělesnou výchovou, výchovou ke zdraví a dalšími předměty.
Úvod
Jízdní kolo (bicykl) je nejen dopravní prostředek, ale nástroj pro cvičení, zvyšování sebekázně, zlepšování psychického stavu. Jeho uživatel/majitel by měl v pravidelných intervalech provést jeho základní údržbu. V případě poruchy na cestách prověřuje technické schopnosti jeho uživatele při jejím odstraňování. K uvedeným skutečnostem navíc přispívá fakt, že jízdní kolo v základní konfiguraci je většině populace cenově dostupné.
Jízdní kolo
Pokud se na bicykl podíváme z hlediska fyziky a techniky, je na něm spojeno mnoho technických řešení: rozložení látky (poloha těžiště), technika jízdy (v sedle, ze sedla = > proklouznutí zadního kola na štěrku), šlapání do pedálů (kolik toho odkrouží chodidlo => tečna k pedálům), aerodynamický tvar a odpor vzduchu (tvar cyklisty pro časovky na Tour De France), páka (převody), setrvačnost, tření [2].
Všechna z nich využívají základních zákonitostí fyziky, proto je bicykl velmi vhodnou učební pomůckou ve výuce, nejen fyziky, na základní škole. Bicykl tak můžeme použít jako spojovací článek při vytváření mezipředmětových vztahů mezi fyzikou, technickou výchovou, informační výchovou, výchovou ke zdraví a dalšími [2].
Jízdní kolo ve fyzice
Jak jsme již výše uvedli, nalezneme na jízdním kole mnoho prvků a situací, které lze ve výuce fyziky vhodně použít. My se ale nyní omezíme pouze na problematiku těžiště celé soustavy jízdní kolo + cyklista.
Poloha těžiště cyklisty
V současné době, kdy stále více lidí myslí na svoji hmotnost a zdravý životní styl, se musel tento trend promítnout také do cyklistiky. Ve skutečnosti je tomu naopak, v cyklistice je to již dlouho známá věc, že je jednodušší a levnější snížit hmotnost cyklisty než jízdního kola. S tím zároveň souvisí také poloha těžiště.
Tento experiment byl pro nás stěžejní. Snažili jsme se simulovat více situací. Jako první jsme zjišťovali polohu těžiště cyklisty bez jakékoli zátěže. V dalším jsme přidávali do batohu na záda nebo na břicho 3 kg nebo 6 kg zátěž, kterou nám tvořily jedna nebo dvě plastové nádoby vody. V každé konfiguraci proběhlo měření při třech různých výškách zadního kola. To jsme podkládali až třemi kusy dřeva o výšce cca 10 cm. Odečítali jsme z váhy pod předním kolem, jaká hmotnost systému jízdní kolo + cyklista připadá na přední kolo.
Těžiště jízdního kola nalezneme podle I. Krejsy [3] v těchto místech:
- Bez cyklisty - přibližně nad středovým složením a podle druhu jízdního kola, výšky jeho sedla a rozměru kol v rozmezí hodnot 0,33 m až 0,60 m nad vozovkou
- S cyklistou - přibližně nad rovinou sedla v rozmezí hodnot 0,05 m až 0,25 m podle výšky a hmotnosti cyklisty
Při měření polohy těžiště jízdního kola s cyklistou nám tedy vznikaly situace zachycené na Obr. 1-3:

Obr. 1 - Fotografie z měření polohy těžiště jízdního kola s cyklistou – bez zátěže

Obr. 2 - Fotografie z měření polohy těžiště jízdního kola s cyklistou – zátěž na zádech

Obr. 3 - Fotografie z měření polohy těžiště jízdního kola s cyklistou – zátěž na břiše
S využitím vztahů pro jednozvratnou páku s osou otáčení v ose předního kola, přičemž změna průmětu vzdálenosti těžiště od osy otáčení se dá rozložit do průmětu vzdáleností středů kol a do průmětu výšky těžiště do vodorovné spojnice středů kol. Celkovou výšku těžiště s od terénu pak získáme ještě přičtením poloměru kola r.
Naměřené hodnoty jsme dosadili do vztahu (1) z [1]: \[ s= \frac{l(M_{1a}-M_1)}{M\,\mathrm{tg}\,\alpha}+r .\]
kde:
l – vzdálenost středů kola
r – poloměr kola
M1 – hmotnost zjištěná na váze na předním kole nenakloněného jízdního kola
M1a – hmotnost zjištěná na váze na předním kole nakloněného jízdního kola
M – hmotnost kolo + cyklista + zátěž
α – náklon kola, tg α můžeme určit např. jako poměr výšky zvednutí zadního kola a vodorovném průmětu vzdáleností obou os, kterou můžeme snadno získat např. zavěšením olovnic na osy.
Těžiště získaná z měření jsou na obrázcích Obr. 4-8 vždy naměřena pro čtyři výšky zadního kola oproti přednímu, a to v těchto výškách: T1x = -8 cm; T2x = 2 cm; T3xx = 12 cm; T4x = 22 cm, index x odpovídá danému případu.
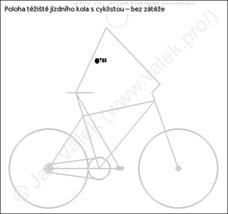
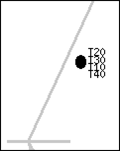
Obr. 4 - a) Poloha těžiště jízdního kola s cyklistou – bez zátěže b) Zvětšený obrázek polohy těžiště 2:1

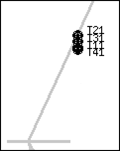
Obr. 5 - a) Poloha těžiště jízdního kola s cyklistou – zátěž 3 kg na zádech b) Zvětšený obrázek polohy těžiště 2:1

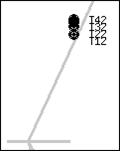
Obr. 6 - a) Poloha těžiště jízdního kola s cyklistou – zátěž 6 kg na zádech b) Zvětšený obrázek polohy těžiště 2:1

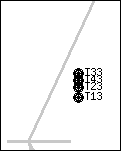
Obr. 7 - a) Poloha těžiště jízdního kola s cyklistou – zátěž 3 kg na břiše b) Zvětšený obrázek polohy těžiště 2:1

Obr. 8 - a) Poloha těžiště jízdního kola s cyklistou – zátěž 6 kg na břiše b) Zvětšený obrázek polohy těžiště 2:1
Jak je patrné z obrázků Obr. 4-8, výška těžiště s se mění v závislosti na zátěži cyklisty, vodorovná poloha l2 se výrazně nemění, její hodnotu určíme pomocí vztahu pro jednozvratnou páku se středem otáčení v ose předního kola (2): \[ l_2 = \frac{M_1}{M} l \] kde: l – vzdálenost os otáčení předního a zadního kola bicyklu; M1 – hmotnost zjištěná na váze na předním kole nenakloněného jízdního kola; M – hmotnost kolo + cyklista + zátěže
Závěr
První příklad jsme prakticky prováděli s žáky 9. třídy v rámci přípravy na přijímací zkoušky na střední školy. Žáci sami zjišťovali podklady a podíleli se výraznou měrou na uskutečnění celého pokusu. Teoretická příprava byla ponechána jako domácí práce žákům. Před měřením proběhlo zopakování celého úkolu. Vlastní měření se zvládlo za cca 45 minut.
Se žáky lze dále diskutovat vliv rozložení látky na jízdu, jaká je poloha těžiště automobilů (osobní, nákladní, závodní), kdy dojde k zablokování předního kola a cyklista přepadne přes řidítka, a mnoho dalších technicko-sportovních aspektů.
Literatura
[1] Cibula, K. Mechanika jízdního kola. 2. vyd. Praha: ČVUT v Praze, 2004. 93 s. ISBN 80-01-03016-4.
[2] Kašpar, E., Janovič, J., Březina, F. Problémové vyučování a problémové úlohy ve fyzice. 1. vyd. Praha: Státní pedagogické nakladatelství, n. p., 1982. 364 s.
[3] Krejsa, I. Metodická pomůcka k řešení nehody s účastí cyklistů. In: IKOS Znalecká kancelář [online]. 2012 [cit. 2013-08-01]. Dostupné z: http://www.crash.cz/admin/files/ModuleText/3-Metodicka-pomucka-k-reseni-nehody-s-ucasti-cyklistu.pdf