O příspěvku
PDF ke stažení2 v 1 – úlohy experimentální i teoretické
Abstrakt
V tomto příspěvku jsou uvedeny tři úlohy, které je možné v rámci středoškolské fyziky řešit jak experimentálně, tak teoreticky. Tyto úlohy byly prověřeny ve vyučovací praxi. Teoretické a experimentální metody jsou pro fyziku jako vědu typické a z hlediska poznávacích procesů mohou být pro žáky velmi přínosné.
Úvod
Ve výuce fyziky mají své místo jak experimentální, tak teoretické metody řešení problémů. Dost často jsou tyto přístupy chápány – zejména žáky – odděleně. Přitom síla a krása experimentů a teorií je v tom, že se vzájemně doplňují a podporují. V tomto příspěvku se snažíme na příkladu tří fyzikálních úloh ukázat, že jejich řešení je možné provést „zároveň“ teoreticky a experimentálně. V některých případech je lépe začít pokusem, jindy je přístupnější vydat se na začátku teoretickou cestou.
1 Zrcadlo na válcovém sloupu[1]
Zadání
V některých novějších prostorách – v obchodních centrech, modernizovaných nádražních halách nebo v pražském metru (např. stanice „Rajská zahrada“ na trase B) – jsou sloupy tvaru válce, jejichž povrch je z lesklého kovu. Jak se uvidí člověk, který stojí před takovým sloupem?
Experimentální řešení
Pokus můžeme uspořádat tak, že vyrobíme model sloupu s lesklým kovovým povrchem. Použít můžeme v podstatě libovolný válcový předmět, na který navineme hliníkovou fólii používanou v kuchyni („alobal“). Můžeme ji připevnit třeba izolepou. Pokud k fólii přiblížíme např. prsty nebo obličej, vidíme, že jejich obraz je vzpřímený, stejně velký (vysoký) a užší („hubenější“) než předmět. Pravá a levá strana není zaměněna. Ke stejnému výsledku dospějeme, pokud použijeme k experimentu např. hrnec z lesklé nerezové oceli. Jinou možností je najít zmíněný sloup v terénu, stoupnout si před něj a pozorovat.
Teoretické řešení
Při teoretickém řešení je potřeba si uvědomit, že ve směru, ve kterém není zrcadlo zakřivené (zde svislý) bude zobrazovat jako rovinné zrcadlo, zatímco ve směru, ve kterém je zakřiveno (zde vodorovný), bude zobrazovat jako vypuklé zrcadlo (jedná se totiž o vnější povrch válce). Předmět (člověk) zůstane proto stejně velký a vzpřímený (vlastnosti rovinného zrcadla), ale bude užší („hubenější“), protože vypuklé zrcadlo zmenšuje. Pravá a levá strana nebude zaměněna, protože vypuklé ani rovinné zrcadlo nepřevrací.
Odpověď
Jak experimentálně, tak teoretickým rozborem jsme dospěli k tomu, že v zrcadle, které je na vnějším povrchu válce, se uvidí člověk jako vzpřímený, stejně velký (vysoký) a užší („hubenější“). Nezáleží na vzdálenosti člověka od zrcadla.
Metodické poznámky
V teoretické části se jedná o úlohu jednak na analýzu (na válcové zrcadlo můžeme pohlížet jako na rovinné a vypuklé zrcadlo zároveň), jednak na syntézu (dílčí poznatky o zobrazování těmito zrcadly musí žáci spojit).
2 Vytékání vody z boku láhve
Zadání
V boku půllitrové PET láhve uděláme asi ve třech čtvrtinách její výšky malý kruhový otvor o průměru asi 1 mm. Láhev naplníme vodou. Hrdlo láhve zůstane otevřené. Voda vytéká malým otvorem. Jak pokus po několika minutách skončí?
Experimentální řešení
Otvor do plastové láhve uděláme např. špendlíkem, který zahřejeme v kleštích nad plamenem čajové svíčky. Naplníme-li láhev vodou, pozorujeme nejprve, že se voda vytékající z láhve pohybuje obdobně jako při vodorovném vrhu. Při dostatečném poklesu hladiny v láhvi začne voda stékat po jejím povrchu. Překvapením může být, že voda přestane vytékat, když je hladina přibližně 8 mm nad otvorem (obr. 1), což nastane po necelých 10 minutách.

Obr. 1 Hladina se ustálí téměř 1 cm nad otvorem (zvýrazněn uprostřed)[2]
Teoretické řešení
Díky tomu, že je otvor malý, projeví se zde pružnost povrchu vody. Při poklesu hladiny klesá hydrostatický tlak v místě otvoru a při určité (dostatečně malé) hloubce otvoru pod volnou hladinou nastane rovnováha mezi hydrostatickou tlakovou silou a povrchovou silou (obě působí v otvoru).[3]
Odpověď
Experiment dopadl překvapivě; nevytekla všechna voda nad otvorem, ale hladina se ustálila téměř 1 cm nad ním. Teoreticky to můžeme vysvětlit tím, že se povrch kapaliny chová jako pružná blána.
Metodické poznámky
Pokus je vhodné několikrát zopakovat. Je možné experimentovat s otvory různých průměrů (při dostatečně velkých už ke zmíněnému jevu nedojde). Úloha je vhodná k integraci učiva mechaniky tekutin a molekulové fyziky.
3 Plachetnicí proti větru[4]
Zadání
Demonstrujte a vysvětlete, jak může plachetnice plout částečně proti větru.
Experimentální řešení
Model plachetnice můžeme sestrojit z běžně dostupného materiálu, zejména kancelářských potřeb. Použít můžeme pouzdro na mýdlo, plastové desky, brčko, špejli, kancelářské svorky, papír a izolepu (obr. 2). Podstatné je, aby se mohla plachta při experimentu nastavit do vhodného úhlu, a dále je potřeba udělat velký kýl (je z plastových desek a bude pod hladinou). Když budeme do papírové plachty loďky foukat ústy přibližně podle obr. 3 (na což bychom měli experimentálně přijít), rozjede se (ve vaně nebo v jiné hlubší nádobě s vodou) ve směru své podélné osy. Plachetnice se tak částečně pohybuje proti směru, kterým „fouká vítr“.

Obr. 2 Jeden z možných modelů plachetnice
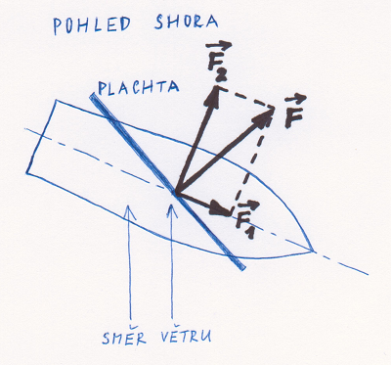
Obr. 3 Náčrtek plachetnice s působícími silami
Teoretické řešení
Působící síly si znázorníme do obrázku (obr. 3). Vítr působí na plachtu tlakovou silou \(\vec{F}\) kolmo k ní (její rovině). Tato síla se rozkládá do složky \(\vec{F}_1\), která míří ve směru podélné osy plachetnice, a složky \(\vec{F}_2\) ve směru kolmém k podélné ose. Síla \(\vec{F}_1\)způsobuje pohyb plachetnice dopředu a síla \(\vec{F}_2\) se ruší odporovou silou vody, který je kladen rozlehlému (u skutečných plachetnic hlubokému) kýlu.
Odpověď
Experimentálně i teoreticky jsme ukázali, že plachetnice se může pohybovat částečně proti směru větru. Model naší plachetnice měl relativně velký kýl, ale díky tomu byl výsledek pokusu jednoznačný.
Metodické poznámky
Z hlediska fyzikálního tématu se jedná o pohyb tělesa v prostředí, které mu klade odpor, a o rozkládání sil. Někdy je třeba žákům napovědět, že mají rozkládat sílu, která je kolmá k plachtě, příp. můžeme žákům v rámci zadání poskytnout obr. 3 bez vyznačených sil. Popsaný jev se v praxi využívá při tzv. křižování plachetnice proti větru. Více informací nalezneme v angličtině ve [4].
Závěr
V tomto článku jsme uvedli a diskutovali tři úlohy, k jejichž řešení je možné v rámci středoškolské výuky fyziky přistupovat jak teoreticky, tak také experimentálně. Při zařazování obdobně zaměřených úloh do výuky je potřeba pečlivě vybírat témata; ne vždy totiž mají středoškoláci k vysvětlení určitého experimentu potřebné teoretické znalosti. Při hledání souladu mezi teoretickým a experimentálním řešením je třeba mít na paměti, že teorie vysvětlí experiment mnohdy pouze přibližně.
Literatura
[1] Žák V.: Fyzikální úlohy pro střední školy. Prometheus, Praha, 2011.
[2] Kružík M.: Sbírka úloh z fyziky pro žáky středních škol. SPN, Praha, 1984.
[3] Nahodil J.: Fyzika v běžném životě. Prometheus, Praha, 1996.
[4] http://en.wikipedia.org/wiki/Keel
[1] Úloha je inspirována úlohou C5 ze sbírky [1].
[2] Za pomoc při zhotovení fotografií děkuji Petru Lukešovi.
[3] Z rovnosti velikostí povrchové a hydrostatické tlakové síly dostáváme při daném průměru otvoru a hloubce řádově správnou hodnotu povrchového napětí vody (desítky mN ∙ m–1).
[4] Námět této úlohy najdeme ve [2] na str. 81 a ve [3] na str. 18.