O příspěvku
PDF ke staženíJako zpomalený film …
Abstrakt
Článek popisuje sérii záběrů, které jsme natočili cenově dostupnou rychloběžnou kamerou, a komentuje jejich použití pro motivaci studentů, studium průběhu fyzikálních dějů a měření ve školské fyzice. Článek navazuje na loňský příspěvek s názvem „1200 FPS“[1].
Rychloběžné video
Rychloběžné video nabízí učiteli řadu možností, jak oživit hodiny fyziky zajímavým dějem nebo měřením a přitom je s moderní digitální technikou relativně snadno cenově dostupné.
Všechny rychloběžné klipy popisované v tomto textu byly pořízeny za pomocí rychloběžné kamery CASIO Exilim EX-F1 při snímkové frekvenci 1200 FPS. Klipy lze přehrát ze serveru YouTube z adresy http://bit.ly/videa-veletrh-16.
Pohyb datla
Datel na tyčce, který drží ve své poloze, dokud jej nerozkýveme, a pak se vydá na cestu dolů a do tyče přitom klove, je jedna z mnoha fyzikálních hraček. Chování datla vysvětlujeme pomocí třecí síly, která s datlovou polohou narůstá a opět mizí tak, jak se stojánek s tyčí zaklesnou a opět povolí. Videozáznam nám toto chování potvrdí. Na začátku vidíme, jak se datel dostane do polohy, ve které je tření minimální, padá tak dlouho, než jej tření zastaví a rozkmitá. Dál pak při každém kmitu klesne o malý kousek níž přesně ve chvíli, kdy jeho stojánek není do tyče zaklesnut a tření se neuplatňuje.

Obr. 1 Datel
Setrvačnost míčku
1. Newtonův zákon (a nebo také to, co se děje s nepřipoutaným pasažérem auta) můžeme vysvětlit na pohybu míčku posazeného na korbu autíčka, které nárazem zastaví.
Klip ukazuje, jak v okamžiku nárazu autíčko zůstává na místě, zatímco míček pokračuje dopředu téměř původní rychlostí (a je mírně vymrštěn vzhůru). Ještě lépe je popis děje zřetelný z grafu závislosti rychlosti na čase (graf 1): Horní křivka ukazuje rychlost ve směru osy x – v tomto směru se rychlost téměř nemění s výjimkou dvou míst: Nárazu kvádru, kdy se část energie spotřebuje na vymrštění vzhůru, a dalšího nárazu na desku stolu. Rychlost ve směru osy y je nulová až do okamžiku nárazu a pak lineárně klesá (míček je nejprve brzděn a pak urychlován tíhovou silou).
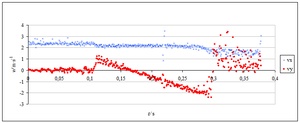
Graf 1 Setrvačnost míčku
Smykové tření
Teorii smykového tření probíráme v mechanice, obvykle v prvním ročníku gymnázia a uvádíme tyto vlastnosti třecí síly:
1. Třecí síla je přímo úměrná síle normálové
2. Třecí síla nezávisí na velikosti styčné plochy
3. Třecí síla nezávisí na vzájemné rychlosti povrchů
S pomocí záznamu z rychloběžné kamery se můžeme pokusit některé z těchto vlastností ověřit. Natočili jsme několik zabrzdění dřevěného kvádru na laminátovém stole a vyhodnocovali jeho zpomalení. Graf 2 zobrazuje analýzu tři různých měření za stejných podmínek. Jednotlivé pokusy se liší jen jinou počáteční rychlostí.
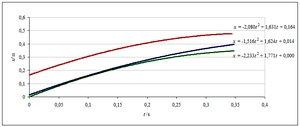
Graf 2 Smykové tření
Vidíme, že všechny křivky odpovídají svým průběhem proložené parabole, jedná se tedy o pohyb s konstantním zpomalením nezávislým na rychlosti (3. vlastnost). Jednotlivá zpomalení jsou nicméně natolik rozdílná (i data z dalších měření mají podobný rozptyl), že prakticky nelze zbývající vlastnosti třecí sily zkoumat a měli bychom si být vědomi toho, že teorie smykového tření a vzorce pro výpočet velikosti třecí síly jsou jen přibližné.
Výskok panáčka
Zajímavým námětem ke zkoumání je fyzikální hračka – panáček na pružině a přísavce, který po přitisknutí ke stolu chvíli stojí na místě a poté se vymrští vzhůru. Popis děje je poměrně jednoduchý: Přísavka přidržuje panáčka na místě a pružina ji postupně odtlačuje. V určitém okamžiku se přísavka uvolní a pružina vymrští celého panáčka vzhůru.
Klip z kamery tento popis děje potvrdí a ukáže nám, jak i po odlepení pružina dále osciluje. Ještě zajímavější je pak pohyb panáčka po dopadu na zem a odrazu od ní – vidíme zde ukázku zákona zachování momentu hybnosti. Pružina nyní osciluje „ze strany na stranu“ a panáček nebo jeho noha s pružinou se střídavě pohybují (rotačním pohybem) a zastavují. Jako celek se ale panáček otáčí, jeho celkový moment hybnosti zůstává zachován.
Leidenfrostův jev
Leidenfrostův jev se odborně nazývá děj, který zná každý, kdo někdy stříkl trochu vody na rozpálenou plotnu. Je-li plotna dostatečně horká, voda místo zasyčení a odpaření utvoří kapičky a v těchto kapičkách se kutálí po plotně. Důvodem pro nezvyklé chování kapiček je prudké odpařování a expanze vodní páry v místě kontaktu s plotnou. Unikající pára pak nadzvedává celou kapku a posunuje ji po jakémsi vzduchovém (či spíše parním) polštáři [2]. Podařilo se nám natočit záběry několika kapek pohybujících se na rozžhaveném elektrickém vařiči a jejich chování studenty často fascinuje.
V prvním videoklipu vidíme kapku, která se po vařiči kutálí a nemůže propadnout mezi jeho spirálami. Stálým vypařováním se zmenšuje objem kapky i povrch vypařování a nakonec již parní polštář kapku neudrží a kapka propadne.
Druhý videoklip zachycuje kapku dopadající na místo, které bylo předchozími kapkami již příliš prochlazeno, takže kapka se po dopadu na vařič rozletí prudkou expanzí do stran rozdělena na mnoho drobných kapiček, které se od vařiče odráží jako pružné míčky.
Galtonova deska
Jde o matematický model „bludiště“ve tvaru trojúhelníku, kterým náhodně propadávají kuličky a hromadí se v několika zásobnících. Fyzikální realizace teoretického modelu byla součástí příspěvku [3].
Kulička se při každém nárazu „rozhoduje“ na kterou stranu se odrazí a pokud je pravděpodobnost odrazu vlevo i vpravo stejná, vede matematické řešení k Pascalovu trojúhelníku. A právě ono „rozhodování“ kuliček jsme zkoumali rychloběžnou kamerou. Odrazy na jednotlivých překážkách (šrouby obalené bužírkou) trvaly různě dlouho (viz videozáznamy). Naměřili jsme nejdelší dobu setrvání kuličky na jednou šroubu 0,25 s. Průchod kuličky všemi devíti řadami šroubů se v demonstrovaném videozáznamu pohyboval od 0,5 s do 1,3 s.
Pružné srážky
Na dvě autíčka jsou upevněny válcové magnety s otvorem uprostřed (např. v mikrovlnné troubě jsou dva) a to tak, aby se odpuzovaly. Jedno autíčko bylo vzhledem k podložce v klidu a druhé na něj najíždělo.

Obr. 2 Srážka autíček s magnety
V prvním pokusu měla obě autíčka stejnou hmotnost. Je vidět, že přijíždějící autíčko se zastaví a druhé autíčko se rozjede. Pružnou srážku názorně znázorňují graf 3 a graf 4.
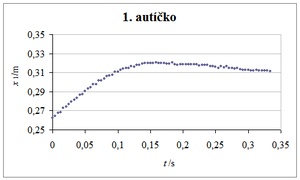
Grafy 3 a 4 Závislost polohy na čase přijíždějícího a původně stojícího autíčka
Z videozáznamu jsme určili rychlost 1. autíčka před srážkou v1 = 0,56 m·s–1, rychlost 2. autíčka byla u1 = 0 m·s–1. Rychlosti po srážce byly v2 = 0 m·s–1, u2 = 0,47 m·s–1. Došlo k poklesu kinetické energie soustavy o 30 %, což nepůjde vysvětlit chybou měření.
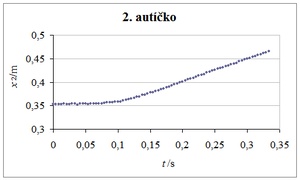
Ve druhém pokusu mělo přijíždějící autíčko menší hmotnost (náklad 1 magnet) a stojící autíčko větší hmotnost (3 magnety). Je vidět, že přijíždějící lehčí autíčko se po interakci vrací zpět a druhé těžší autíčko se dává do pohybu opačným směrem. Pružnou srážku znázorňují graf 5 a graf 6.
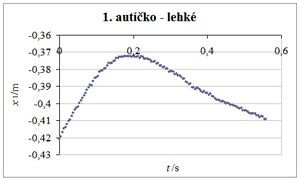
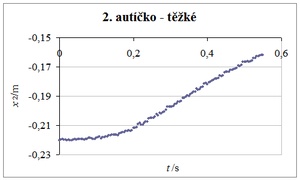
Grafy 5 a 6 Závislost polohy na čase přijíždějícího lehkého a původně stojícího těžkého autíčka
Rychlost 1. autíčka před srážkou byla v1 = 0,37 m·s–1, rychlost 2. autíčka byla u1 = 0 m·s–1. Rychlosti po srážce byly v2 = −0,13 m·s–1, u2 = 0,15 m·s–1. Došlo k poklesu kinetické energie soustavy o 50 %.
Kinetická energie před srážkou byla 0,0146 J a po srážce 0,0071 J. Jak to vysvětlit? Část kinetické energie se zřejmě přeměňovala na polohovou energii tíhovou. Provedli jsme výpočet pro kolečka, která nemají přesně tvar kruhu, respektive nemají osu uprostřed kruhu.

Obr. 3 „Ztráta“ energie zdvihnutím celého autíčka
Pokud se těžší autíčko má zvednout o 1 mm, musí se jeho potenciální energie tíhová zvětšit o 0,0046 J a to je reálné.
Imploze plechovky
Jedním z mnoha způsobů demonstrace přítomnosti a účinků atmosférického tlaku je experiment, ve kterém v nápojové plechovce přivedeme k varu malé množství vody a následně plechovku otvorem dolů ponoříme do studené vody. Okolní voda vychladí vzduch uvnitř, čímž klesne jeho tlak natolik, že okolní vzduch (pod atmosférickým tlakem) plechovku zdeformuje.
V záběrech rychloběžného videa můžeme jev pozorovat detailně a také změřit jeho trvání. Konzerva se začne hroutit po zhruba 150 ms (což je zhruba doba prochlazení plynu uvnitř) a samotné zhroucení trvá 2,5 ms. Rychlost, s jakou děje probíhají, může být poměrně překvapivá vzhledem k tomu, že tepelnou výměnu obvykle vnímáme jako proces velmi pomalý.
Poděkování
Autoři by rádi poděkovali katedře didaktiky fyziky MFF UK za opakované zapůjčení rychloběžné kamery pro natočení videoklipů.
Literatura
[1] Koupil, J.; Vícha, V. 1200 FPS. In Veletrh nápadů učitelů fyziky 15. Sborník z konference. Ed. Z. Drozd. 1. vyd., Praha: Prometheus, 2011. s. 116–121. ISBN: 978–80–7196–417–9.
[2] Halliday, D.; Resnick, R.; Walker, J. Fyzika – Část 2, Mechanika – Termodynamika. 1. vyd., Brno: VUTIUM, 2009. ISBN 80–214–1868–0.
[3] Vícha, V.; Formánek, P. Náhoda v chování fyzikálních objektů Veletrh nápadů učitelů fyziky 10. Sborník z konference. Ed. L. Dvořák. 1. vyd. Prometheus, 2006. s. 180–186. ISBN: 80–7196–331–3