Prokšová J.: Některé pokusy z vlnové optiky (Veletrh 13, Plzeň 2008) / Sborník Veletrhu nápadů učitelů fyziky

O příspěvku

Klíčová slova

Použití

SŠ/VŠ

Pomůcky

S běžným vybavením kabinetu
Se speciálními pomůckami

PDF ke stažení

Některé pokusy z vlnové optiky

Prokšová J.

Příspěvek popisuje tři jednoduché experimenty z vlnové optiky:

• difrakci na zácloně,

• Quételetovy kruhy,

• Pohlův pokus.

1. Difrakční jevy na zácloně

Potřeby: kousek velmi jemné síťoviny („moderní“ typ záclony), svíčka, zápalky.

Rozdáme mezi žáky čtverečky síťoviny (stačí 15 x 15 cm), zapálíme svíčku a zatemníme učebnu. Pak je necháme – nejlépe ze vzdálenosti několika metrů – pozorovat přes kousky síťoviny hořící svíčku. Upozorníme na barevné proměny difrakčních jevů při otáčení síťoviny.

Obr. 1

2. Quételetovy kruhy

Potřeby: přenosný projektor, zrcadlo, kousek vaty, sádrový prach.

Pokus, kterým existenci Quételetových kruhů prokážeme, je na přípravu velmi jednoduchý. Stačí k tomu dokonale zatemněná místnost, intenzivní zdroj světla – např. přenosný projektor Meotar a větší zrcadlo (zhruba 50 x 40 cm), které poklepeme vatou „zašpiněnou“ sádrovým prachem.

Zrcadlo postavíme několik metrů od zdroje (čím větší vzdálenost nám místnost umožňuje tím lépe – barevné kruhy jsou pak širší a dobře rozeznatelné). Místnost zatemníme a zrcadlo osvítíme zdrojem světla. Postavíme se poblíž zdroje (zhruba 0,5 m za zdrojem) a drobnou změnou polohy hlavy hledáme „správnou“ pozici pozorovatele. Někdy zpočátku chvíli trvá, než Quételetovy kruhy na zrcadle objevíme. Pak však už stačí jen pozorně se dívat a natáčet hlavu. Tím dochází k neustálé proměně tohoto zajímavého jevu.

Obr. 2

Poznámka: Quételetovy kruhy můžete spatřit i pokud bydlíte blízko silnice nebo parkoviště na okenní tabulce. V noci je způsobí procházející světlo od reflektoru projíždějícího nebo parkujícího auta. Tento barevný oblouk spektra lze pozorovat také na hladině rybníku v období pylové sezóny.

Matematické pozadí: Hledáme-li vysvětlení, většinou nás nejprve napadne, že podobný jev vzniká interferencí světla na tenké vrstvě. Hlubším zkoumáním však poznáme, že výsledný barevný vjem souvisí nejen s interferencí, ale i s rozptylem světla na prachových částečkách, které okenní tabulku pokrývají. Proto můžeme tyto barevné oblouky spatřit i při dopadu světla na klidnou vodní hladinu, pokrytou drobnými částečkami pylu, nebo na zaprášené zrcadlo.

Na obrázku 3 vpravo (převzat z [1]) je schematicky znázorněna situace, kdy Quételetovy kruhy vznikají v naposledy zmíněném případě, tedy na zaprášeném zrcadle. Pro jednoduchost předpokládejme, že ve vzdálenosti a od zrcadla vychází ze zdroje L monochromatické světlo. Pozorovatel je v bodě O (ve vzdálenosti b od zrcadla) a sklo zrcadla má tloušťku t. Ve vzdálenosti r od bodu F se nachází částečka prachu P.

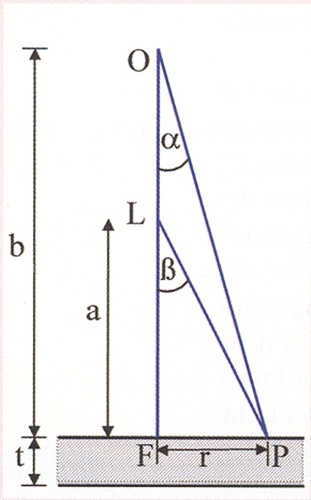
Obr. 3

Obrázek 4 dole (převzat z [1]) ukazuje, že pro výklad vzniku Quételetových kruhů využijeme dva paprsky, které vycházejí ze zdroje L. První z nich (na obrázku označen 1) dopadá na sklo v bodě Q pod úhlem \( \beta \) a láme se do něj podle Snellova zákona pod úhlem \( \beta' \). Po odrazu na zadní straně zrcadla (bod T) dopadá paprsek na prachovou částečku P a díky rozptylu dochází ke změně jeho směru. Ze skla proto vychází rovnoběžně s druhým paprskem pod úhlem \( \alpha' \).

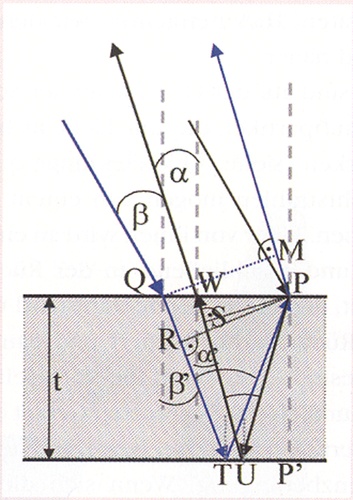
Obr. 4

Druhý paprsek (označen 2) dopadá na sklo přímo v místě, kde je částečka prachu, a rozptyluje se na ní. Na zadní stranu zrcadla dopadá v bodě U, přičemž se odráží zpět do skla. Do bodu S na rozhraní sklo-vzduch pak tento paprsek dopadá pod úhlem \( \alpha' \). Podle Snellova zákona se světlo do původního prostředí – vzduchu – lomí pod úhlem \( \alpha \).

Je zřejmé, že oba paprsky, vystupující ze skla, jsou rovnoběžné a do oka pozorovatele směřují pod úhlem \( \alpha \). Vzniká mezi nimi dráhový rozdíl \[\tag{1} \delta = \Delta s_2 - \Delta s_1, \] kde \( \Delta s_1 = 2\cdot n \cdot t \cdot \cos \alpha' \) a \( \Delta s_2 = 2\cdot n \cdot t \cdot \cos \beta' \) (n je index lomu skla).

Podmínkou interference je, že \[\tag{2} k \cdot \lambda = \delta = \Delta s_2 - \Delta s_1, \] přičemž \( k = 0,\,\pm 1,\,\pm 2,...\).

Předpokládáme-li navíc, že se jedná o malé úhly, můžeme \( \Delta s_1 \) a \( \Delta s_2 \) upravit pomocí vztahů \[\tag{3a} \cos \alpha' = \sqrt{1-\frac{\sin^2 \alpha}{n^2}} \approx 1-\frac{\alpha^2}{2\cdot n^2}, \] \[\tag{3b} \cos \beta' = \sqrt{1-\frac{\sin^2 \beta}{n^2}} \approx 1-\frac{\beta^2}{2\cdot n^2}. \]

Použijeme-li dále přiblížení, že \( \alpha \approx \frac{r}{b} \) a \( \beta \approx \frac{r}{a} \), lze pak \( \Delta s_1 \) a \( \Delta s_2 \) vyjádřit jako \[\tag{4a} \Delta s_1 \approx 2 \cdot n \cdot t \cdot \left(1-\frac{r^2}{2\cdot a^2 \cdot n^2}\right), \] \[\tag{4b} \Delta s_2 \approx 2 \cdot n \cdot t \cdot \left(1-\frac{r^2}{2\cdot b^2 \cdot n^2}\right). \]

Vzhledem k předchozím úvahám můžeme nyní podmínku interference (2) jednoduše přepsat do tvaru \[\tag{5} k \cdot \lambda = \frac{(b^2-a^2)\cdot r^2 \cdot t}{n \cdot a^2 \cdot b^2}. \]

Splňuje-li světlo dopadající na zrcadlo ze vzdáleného reflektoru předchozí podmínku, vznikají na zrcadle typické barevné oblouky – Quételetovy kruhy. Je zřejmé, že pokud pozorovatel změní svou polohu, změní se také sledovaný jev.

Obr. 5

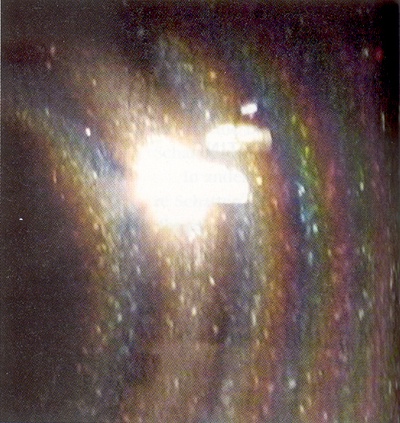
Obr. 6

3. Pohlův pokus

Potřeby: slídová destička z podložky pod výkonový tranzistor, podložka, stojan, sodíková (popř. rtuťová) výbojka

Známý pokus, navržený německým fyzikem Pohlem, lze provést například užitím slídové destičky z podložky pod výkonový tranzistor. Nalepíme ji na podložku, kterou upevníme na stojan. Pak destičku umístíme před sodíkovou výbojku a osvětlíme ji tímto monofrekvenčním světlem. Učebnu předem samozřejmě dokonale zatemníme. Světelné paprsky, které se odrážejí od přední i zadní stěny kousku slídy, interferují. Dochází tak k výraznému jevu – souboru tmavých a světlých oblouků (někdy i půlkruhů). Jsou dobře viditelné na vzdáleném stínítku, kterým může být i jedna ze stěn místnosti. Je zřejmé, že čím je vzdálenost zdroje a slídové destičky od stěny (stínítka) větší, tím se od sebe sousední oblouky více vzdalují (až o několik centimetrů).

Při použití bílého světla se oblouky překrývají, interferenci nelze téměř vůbec pozorovat.