O příspěvku
PDF ke staženíUkázka laboratorních prací měřených soupravou ISES
V roce 1999 byla na našem gymnáziu zřízena počítačová pracovna fyziky vybavená dvanácti počítači Celeron 360 MHz, 80MB RAM, síťovým propojením, kartou ISES standard a řadou měřicích modulů. V této pracovně se měří laboratorní práce z elektřiny a magnetismu ve 3. ročníku čtyřletého studia a ve fyzikálním semináři. Ve třetím ročníku je třída rozdělena na polovinu a u každého počítače tak jsou dva až tři studenti. V případě potřeby může měřit i celá třída, neboť kapacita učebny je 33 míst.
Máme zpracovány návody ke 13 úlohám z elektřiny a magnetismu: řazení kondenzátorů, odpor kovového vodiče, řazení rezistorů, elektrický zdroj napětí, fotorezistor, termistor, polovodičová dioda, elektrolytický vodič, R,C v obvodu střídavého proudu, rezonance v obvodu RLC, polovodičový usměrňovač, vybíjecí křivka kondenzátoru, elektromagnetický oscilátor.
Systém ISES studenti před započetím laboratorních prací znají pouze částečně z některých demonstračních pokusů prováděných učitelem nebo jej sami ovládají při jednoduchých frontálních úlohách. V počátečních úlohách je proto využíváno jen málo možností ISESu, postupně jsou však úlohy náročnější. V závěrečných úlohách se využívá i nástrojů integrál, regrese exponenciální funkcí, rozmítač, zobrazení veličiny vypočtené přímo při měření z aktuální hodnoty jiné veličiny. Praxe ověřila, že při tomto přístupu zvládnou úlohy všichni studenti.
Studenti postupují podle natištěných návodů, učitel má k dispozici verzi, ve které jsou již naměřené výsledky. Při dodržení předepsaného postupu naměří libovolná skupina s náhodně vybranými pomůckami na libovolném počítači výsledky, které se velmi blíží těm, které má uvedeny učitel. Studenti navíc postupují samostatně podle návodů a učitel je jen koordinátorem.
Na naší škole proběhla také školení pro učitele středních škol, při kterých si mohli učitelé měření vyzkoušet. Na těchto setkáních vznikl požadavek, zda by se tato sada úloh nedala rozšířit na další školy. Autor tedy sepsal sbírku: Laboratorní práce k učebnici Elektřina a magnetismus měřené soupravou ISES, doplněnou o disketu konfiguračních souborů a naměřených experimentů, kterou lze zakoupit u autora systému ISES Dr. Lustiga (MFF UK).
Vedle uvedených třinácti úloh z elektřiny máme již zpracovány i jednodušší laboratorní a frontální práce pro nižší gymnázium a několik úloh z mechaniky pro první ročník čtyřletého studia. Ve svém příspěvku bych právě chtěl ukázat měření pohybu kuličky po nakloněné rovině, měření tíhového zrychlení z volného pádu a vybíjení kondenzátoru přes rezistor.
Při všech laboratorních pracích je snahou, aby se fyzika nezměnila na pouhé odklepávání kláves, ale aby studenti chápali výhody využití počítače k reálným měřením, které jsou tradičními prostředky (stopky, ampérmetry, jednoduché osciloskopy) prakticky nemožné. Počítač navíc umožňuje zpracování výsledků např. pomocí Excelu, který má mnoho studentů na svém domácím počítači.
Kulička na nakloněné rovině
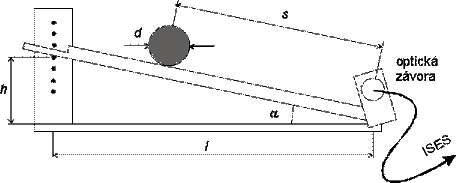
Pomůcky: nakloněná rovina, ocelová kulička, ISES, modul optická závora, soubor: kulicka2.imc.
Úkoly:
1. Proměřit, jak závisí rychlost kuličky valící se po nakloněné rovině na dráze. Provést pro výšky 10 cm až 4 cm. Určit zrychlení kuličky pro jednotlivé úhly nakloněné roviny.
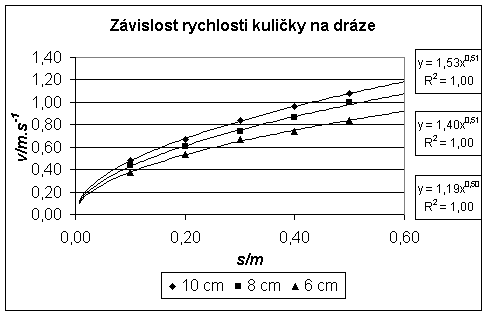
2. Pro výšky 10 cm, 8 cm a 6 cm sestrojit do jednoho obrázku grafy: Závislost rychlosti kuličky na dráze.
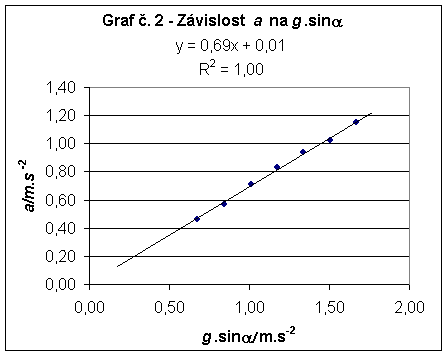
3. Sestrojit graf: Závislost zrychlení na sinu úhlu α a určit koeficient k ve vztahu a = k g sin α.
Teorie:
Pro rovnoměrně zrychlený pohyb začínající z klidu platí 
, kde s je dráha kuličky na nakloněné rovině, a je zrychlení a v je okamžitá rychlost. Rychlost lze určit ze vztahu 
, neboť Δt bude řádu setin sekundy.
Protokol: 1) 2) Tabulka. č. 1 - Závislost rychlosti kuličky na dráze
d = 0,026 m, l = 0,58 m
h/m |
α/rad |
s/m |
0,10 |
0,20 |
0,30 |
0,40 |
0,50 |
průměrné zrychlení |
0,100 |
0,1707 |
Δt/s |
0,054 |
0,039 |
0,031 |
0,027 |
0,024 |
|
v/m.s-1 |
0,48 |
0,67 |
0,84 |
0,96 |
1,08 |
a/m.s-2 |
||
a/m.s-2 |
1,15 |
1,12 |
1,18 |
1,15 |
1,17 |
1,15 |
||
0,090 |
0,1539 |
Δt/s |
0,057 |
0,041 |
0,033 |
0,029 |
0,026 |
|
v/m.s-1 |
0,46 |
0,63 |
0,79 |
0,90 |
1,00 |
|||
a/m.s-2 |
1,06 |
0,99 |
1,04 |
1,01 |
1,00 |
1,02 |
||
0,080 |
0,1371 |
Δt/s |
0,060 |
0,043 |
0,035 |
0,030 |
0,026 |
|
v/m.s-1 |
0,43 |
0,60 |
0,74 |
0,87 |
1,00 |
|||
a/m.s-2 |
0,92 |
0,90 |
0,91 |
0,95 |
1,00 |
0,94 |
||
0,070 |
0,1201 |
Δt/s |
0,065 |
0,046 |
0,037 |
0,032 |
0,027 |
|
v/m.s-1 |
0,40 |
0,57 |
0,70 |
0,81 |
0,96 |
|||
a/m.s-2 |
0,80 |
0,81 |
0,82 |
0,82 |
0,92 |
0,83 |
||
0,060 |
0,1031 |
Δt/s |
0,069 |
0,049 |
0,039 |
0,035 |
0,031 |
|
v/m.s-1 |
0,38 |
0,53 |
0,67 |
0,74 |
0,84 |
|||
a/m.s-2 |
0,72 |
0,70 |
0,75 |
0,68 |
0,71 | 0,71 |
||
0,050 |
0,0860 |
Δt/s |
0,076 |
0,054 |
0,044 |
0,038 |
0,035 |
|
v/m.s-1 |
0,34 |
0,48 |
0,59 |
0,68 |
0,74 |
|||
a/m.s-2 |
0,58 |
0,58 |
0,58 |
0,58 |
0,55 |
0,57 |
||
0,040 |
0,0689 |
Δt/s |
0,084 |
0,061 |
0,049 |
0,043 |
0,038 |
|
v/m.s-1 |
0,31 |
0,43 |
0,53 |
0,60 |
0,68 |
|||
a/m.s-2 |
0,48 |
0,46 |
0,47 |
0,45 |
0,46 |
0,46 |
3) Tabulka č. 2 - Závislost zrychlení na g·sin α
α/rad |
g.sin α |
α/m.s-2 |
0,1707 |
1,67 |
1,15 |
0,1539 |
1,50 |
1,02 |
0,1371 |
1,34 |
0,94 |
0,1201 |
1,18 |
0,83 |
0,1031 |
1,01 |
0,71 |
0,0860 |
0,84 |
0,57 |
0,0689 |
0,67 |
0,46 |
Závěr
Grafu závislosti dráhy kuličky na čase nejlépe odpovídají mocninné funkce, koeficient determinace je pro všechny sklony 1,00. Až na dalších desetinných místech by se projevila odchylka od jedné. Mocnitel nabýval hodnot 0,51; 0,52; 0,49 , což znamená téměř přesně druhou odmocninu. Tím se potvrzuje vzorec . Při větším sklonu má rychlost při stejné dráze větší hodnotu. Pro každý sklon je vypočteno pět zrychlení, které se od průměru liší v řádu jednotek procent. Odchylky jsou zapříčiněny přesností, s níž jsou měřeny veličiny Δt, d, h, l.
Pomocí regrese lineární funkcí se podařilo určit koeficient k: a = 0,69.g.sin α.
Podle teorie má platit: a = 0,71.g.sin α.
Odchylka činí 3%. Kromě přesnosti měření uvedených veličin se na odchylce také podílí, nakolik je experimentální stůl vodorovný. Jistý vliv sehrávají i nerovnosti nakloněné roviny a s nimi spojený valivý odpor.
Volný pád -Výpočet g z volného pádu
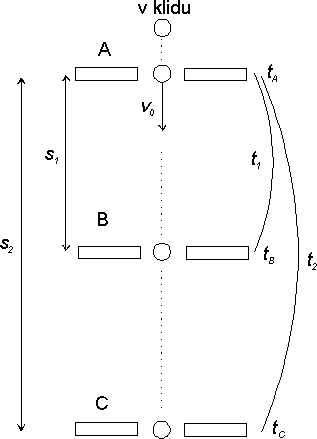
Těleso je volně puštěno nad bodem A. V bodech A, B, C jsou umístěny fotobuňky, které změří časy průletu tělesa např: tA = 0,125 s, tB = 0,304 s, tC = 0,403 s.
AB = s1 = 0,30 m, AC = s2 = 0,60 m jsou vzdálenosti fotobuněk.
Určete hodnotu tíhového zrychlení g.
Řešení:
Pohyb mezi body A a C je rovnoměrně zrychlený se zrychlením g a počáteční rychlost v bodě A je v0. Platí tedy pro něj rovnice
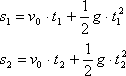
kde t1, t2 jsou časy, které vypočítáme:
t1 = tB – tA = 0,179 s,
t2 = tC – tA = 0,278 s.
Dosadíme do rovnic
0,30 = v0·0,179 + 0,5·g·0,1792
0,60 = v0·0,278 + 0,5·g·0,2782
Vzniklou soustavu rovnic vyřešíme dosazovací metodou. Vyjde
g = 9,74 ms-2.
Co se stane, jestliže všechny hodnoty zůstanou stejné, jen čas tB se zvětší o tři tisíciny sekundy?
tB = 0,307 s
Řešením soustavy získáme
g = 10,62 m.s-2.
Je vidět, že malá chyba v měření jednoho času způsobí velkou chybu g. Proto je lepší provést měření ve více než ve třech bodech.
Přes jedinou fotobuňku (optickou závoru) bude padat těleso podobné hřebenu, jehož polohu určíme podle zatmění infračerveného paprsku každým zubem.
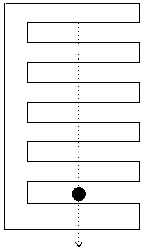
Je třeba určit vzdálenost dvou následujících hran zubů, které zakryjí paprsek.
Pomůcky: hřeben, pravítko, zátěž, počítač, ISES, modul optická závora.
Úkoly:
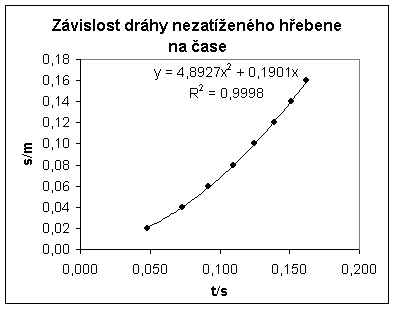
1. Proměřit závislost dráhy padajícího hřebene na čase pro hřeben bez zátěže a pro hřeben se zátěží. Sestrojit graf: Závislost dráhy nezatíženého hřebene na čase.
2. Určit tíhové zrychlení tabulkovým procesorem Excel – regrese kvadratickou funkcí
3. Skupinovou metodou určit tíhové zrychlení pro hřeben padající bez zátěže a se zátěží.
Teorie:
Jednotlivé zuby hřebene při volném pádu přerušují paprsek optické závory. Ze „zhušťování“ grafu lze usoudit, že jde o zrychlený pohyb. Pro jeho dráhu, při zanedbání odporu vzduchu, platí rovnice:
.
Veličina v0 představuje rychlost, kterou vstupuje hřeben do optické závory, t je čas měřený od okamžiku, kdy první zub vstoupil do optické závory.
Regrese kvadratickou funkcí
Jestliže sestrojíme graf Závislost dráhy volného pádu na čase, můžeme využít tabulkový procesor Excel k regresi y = ax2 + bx. Zřejmě platí a = 1/2 g a b = v0.
Skupinová metoda zpracování výsledků
Pro rovnici s = v0t + 1/2 gt2 měříme s a t. Jako neznámé zůstávají veličiny v0 a g. Pokud by byly veličiny s a t přesné, stačily by nám dvě dvojice [t; s] k sestavení dvou rovnic o dvou neznámých a k jejich vyřešení. Protože však naměřené veličiny obsahují určitou chybu, sestavíme tolik rovnic, kolik máme uspořádaných dvojic [t; s].
Např. máme tabulku o čtyřech řádcích
s/m |
t/s |
0,0750 |
0,069 |
0,0833 |
0,075 |
0,0917 |
0,081 |
0,1000 |
0,085 |
z níž lze sestavit 4 rovnice
0,0750 = 0,069·v0 + 0,0023805·g
0,0833 = 0,075·v0 + 0,0028125·g
0,0917 = 0,081·v0 + 0,0032805·g
0,1000 = 0,085·v0 + 0,0036125·g
Rozdělíme rovnice do dvou skupin (jsou dvě neznámé). Sečteme první dvě rovnice a druhé dvě rovnice a každou vynásobíme 1000
158,3 = 144·v0 + 5,193·g
191,7 = 166·v0 + 6,893·g
Vyřešíme soustavu například dosazovací metodou. Vyjde g = 10,16 m.s-2, v0 = 0,733 m.s-1. Takto získané g a v0 se opírá o čtyři měření a má větší váhu než výsledek z pouhých dvou měření. Ještě větší váhu bude mít výpočet založený na tabulce s 8 řádky.
Protokol:
Počet zubů 10, celková délka hřebene 0,20 m, vzdálenost sousedních zubů 0,02 m
Tabulka - Závislost dráhy hřebene na čase
s/m |
t/s (bez zátěže) |
t/s (se zátěží) |
0,02 |
0,048 |
0,035 |
0,04 |
0,073 |
0,059 |
0,06 |
0,092 |
0,076 |
0,08 |
0,110 |
0,094 |
0,10 |
0,125 |
0,108 |
0,12 |
0,139 |
0,120 |
0,14 |
0,151 |
0,133 |
0,16 |
0,162 |
0,144 |
regrese: |
g = 9,79 m.s-2 |
g = 9,95 m.s-2 |
skup. metoda: |
g = 9,68 m.s-2 |
g = 9,98 m.s-2 |
Závěr:
Z grafu závislosti dráhy na čase lze subjektivně posoudit, že body lze proložit křivkou podobnou parabole, což odpovídá rovnici s = v0t + 1/2 gt2. Po provedení kvadratické regrese z hodnoty koeficientu determinace R2 = 0,9998 objektivně vyplývá, že body leží velmi blízko paraboly.
Hodnoty g vypočtené regresí i skupinovou metodou se při porovnání s hodnotou g = 9,81m.s-2 liší maximálně o 1,7 % a to při pádu bez zátěže i se zátěží. Protože odpor vzduchu je na tak krátké dráze zanedbatelný, demonstrovali jsme, že volný pád nezávisí na hmotnosti padajícího tělesa.
Zdrojem chyb může být odečítání časů z monitoru, zuby hřebenu nemusí padat kolmo na svislý směr. Ke zpřesnění by jistě pomohlo, pokud by vzorkovací frekvence mohla být vyšší než 1000 Hz.
Vybíjecí křivka kondenzátoru
Pomůcky: Systém ISES, moduly: ampérmetr, capacity-meter, kondenzátor na destičce, regulovatelný zdroj elektrického napětí (např. PS – 302A), přepínač, sada rezistorů, 6 spojovacích vodičů, soubor: vybij2.imc.
Úkoly:
1. Porovnat vybíjecí křivky téhož kondenzátoru pro rezistory 500 Ω,1 kΩ, 2 kΩ.
2. Určit kapacitu kondenzátoru z náboje a napětí.
3. Určit kapacitu kondenzátoru aproximací vybíjecí křivky.
4. Určit kapacitu kondenzátoru capacity-metrem.
Teorie:
Měření budeme provádět podle obr. 1.
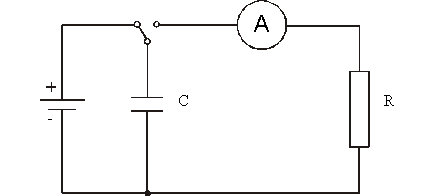
Obr. 1
Při přepnutí do pravé polohy se kondenzátor odpojí od zdroje a vybíjí se přes připojený rezistor. Proud klesá exponenciálně podle rovnice
, kde 
.
Napětí U0 je počáteční napětí, na které se nabije kondenzátor.
V grafu: „Závislost proudu na čase“ lze počáteční náboj kondenzátoru Q0 určit jako plochu pod vybíjecí křivkou, tedy integrací 
.
Pro kapacitu kondenzátoru pak platí 
.
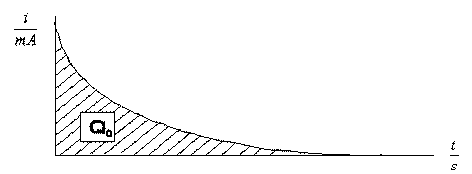
Provedeme-li v ISESu regresi exponenciální funkcí y = a·ebx + c, platí zřejmě b = - 1/(RC) a kapacitu lze vypočítatC = - 1/(bC).
Protokol:
2), 3) Tabulka č 1: Kapacita určená integrací a aproximací
R / kΩ |
1,0 |
1,5 |
2,0 |
2,5 |
Q0 / μC |
64,21 |
63,99 |
69,13 |
69,95 |
I0 / mA |
8,996 |
5,961 |
4,884 |
3,963 |
U0 / V |
8,996 |
8,942 |
9,768 |
9,908 |
b / s-1 |
140,59 |
93,52 |
70,13 |
55,64 |
Cint / μF |
7,14 | 7,16 |
7,08 | 7,06 |
Capr / μF |
7,11 |
7,13 |
7,13 |
7,19 |
Kapacita určená integrací: Cint. = (7,11 ± 0.04) μF , δCint = 0,6 %
Kapacita určená aproximací: Capr = (7,14 ± 0.03) μF , δCapr = 0,4 %
Kapacita určená capacity-metrem: C = 6,85 mF
Závěr:
Pro menší odpor začíná vybíjecí křivka vyšším proudem, ale rychleji klesá k nulovému proudu. Při větší hodnotě odporu probíhá vybíjení déle. Plocha pod křivkou, která představuje počáteční náboj na kondenzátoru, je vždy přibližně stejná.
Kapacita určená integrací Cint je větší než C o 3,8 % a kapacita určená aproximací Capr je větší než C o 4,2%. U obou metod chybu výsledku zřejmě ovlivňuje vybíjecí proud dielektrikem kondenzátoru a také fakt, že vybíjení trvá nekonečně dlouho, zatímco graf na obrazovce končí v konkrétním čase 0,05 s. Určitá „rozházenost“ grafu při proudu blížícím se nule souvisí s obecnou vlastností měřicích přístrojů, které na počátku rozsahu měří s největší relativní chybou. Dopouštíme se také chyby v určení I0 a následného výpočtu U0 z odporu, u něhož počítáme se jmenovitou, nikoli měřenou hodnotou. Na Capr má vliv výběr bodů na křivce, neměli bychom volit body v oblasti nepatrného proudu. Největší zanedbání ale spočívá v tom, že neuvažujeme odpor ampérmetru (je asi 10 Ω) a ani přechodový odpor ve spínači v okamžiku sepnutí. Skutečný odpor obvodu je tedy větší a kapacita je menší než vypočtená.