O příspěvku
PDF ke staženíDeset válců a podnětů k přemýšlení
V době výpočetní techniky, mikroprocesorem řízených spotřebičů a elektronických (vý)tvorů Tamagoči je jaksi zpozdilé nabízet žáku pohled na jednoduchý válec, kutálející se po stole. Několik dobrých důvodů k takovému postupu se ale nabízí:
1. Válec můžeme pozorovat, potěžkat, změřit a zvážit, popsat přesně jeho vzhled.
2. Pohyb válce po nakloněné rovině lze měřit, jiné efekty podrobně popsat.
3. Válec je možné porovnat s dalším, velmi podobným a zjistit rozdíly v pohybu.
4. Můžeme vyslovit domněnky o příčině rozdílů v chování objektů.
5. Válec lze rozebrat a bez nebezpečí poškození zase složit v celek.
6. Je-li k dispozici (na střední škole jistě) dostatečná úroveň fyzikální teorie, lze měřením a výpočtem potvrdit vyslovenou hypotézu.
7. Válečky jsou levné a může je dostat do rukou každý žák.
Jde zřejmě o práci s jednoduchými černými skřínkami. Sedm výše uvedených bodů jen dokládá rozvíjení fyzikálního pohledu na objekt a jeho chování.
Válec 1.
Celý váleček má délku L = 60 mm, průměr D = 40 mm a hmotnost m = 72,6 g. Z toho ocelový váleček má hmotnost m0 = 39,4 g.
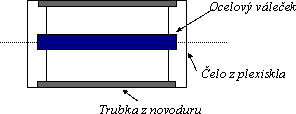
Po nakloněné rovině o délce l = 0,9 m a výšce h = 1,0 cm se skutálí za čas t1 = 4,2 s.
Válec 2.
Parametry druhého válce jsou stejné, pouze ocelový váleček nahradila měděná trubka stejné hmotnosti.
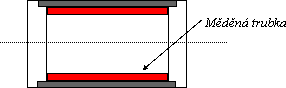
Po nakloněné rovině se tento válec skutálí za delší čas t2 = 4,4 s. Je výhodné pouštět oba válečky současně, zpožďování druhého válce je pak zřetelné.
Kvalitativní vysvětlení objeví žáci sami: druhý váleček má více hmoty uloženo ve větší vzdálenosti od osy otáčení a stejnou kinetickou energii bude mít při menší výsledné rychlosti na konci nakloněné roviny.
Kvantitativní hodnocení lze provést až se znalostí momentu setrvačnosti J s použitím zákona zachování energie:
Potenciální energie v tíhovém poli na počátku pohybu je rovna kinetické energii na konci nakloněné roviny:
m·g·h = ½ J·ω2 + ½ m·v2
Válec 3.
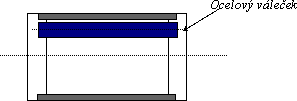
Je stejný jako válec první, jen ocelová vložka je umístěna mimo osu. Jeho chování pozorujeme:
a) při pohybu po vodorovné rovině – pohyb je nerovnoměrný, váleček mění rychlost otáčení,
b) na nakloněné rovině – z jisté polohy se váleček valí několik centimetrů do kopce!
c) na nakloněné rovině – z jisté polohy se váleček trhaně valí dolů.
Chování tohoto objektu lze využít při výkladu rovnovážné polohy. U žáků vzbudí úsměvy a živý zájem.
Válec 4.
Metr dlouhý provázek uchopíme na koncích a mírně napneme. Třecí síly udrží váleček v libovolném místě provázku. Lehce povolíme napětí provázku – a váleček zdánlivě bez příčiny klouže dolů. Zase jej můžeme zastavit kdekoliv. Zvětšení napětí v provázku žáci ovšem nepostřehnou, takže objekt se chová na první pohled zcela záhadně.
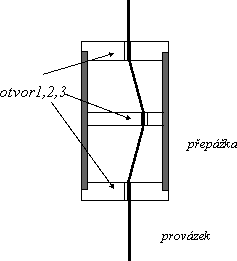
Úkol pro žáky: navrhnout vnitřní uspořádání válečku, které by vysvětlilo jeho chování.
Nakonec vše rozebereme a znovu složíme.
Válec 5. a 6.
V obou válečcích je vidět olověnou kuličku. Zajímavé chování ukazují teprve při plavání na vodě: jeden lze naklopit tmavým nebo čirým čelem vzhůru, druhý je vždy nakloněn tak, že vzhůru míří tmavé čelo. Přepážka vymezující polohu přítěže není na první pohled patrná.
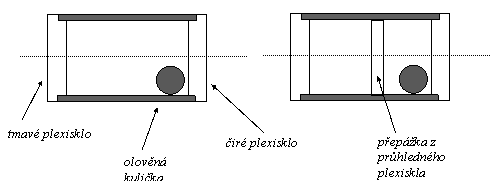
Válec 7. a 8.
Dvojice identických válečků je opatřena permanentními magnety uvnitř, jak ukazuje nákres. Na vodorovné desce stolu se někdy valí k sobě, jindy se odpuzují. Zajímavé je chování na dvou nakloněných rovinách: při malém sklonu je váleček „vyhnán“ z nejnižší polohy, nebo se druhý z válečků přibližuje a zase vzdaluje.
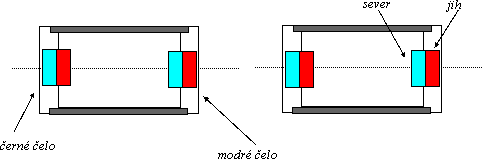
Čela lze zaměňovat a získat i jiné efekty. Žáci zabývající se právě magnetickými jevy naleznou podstatu rychle, důležitá je možnost manipulace s objekty a vnímání sil vlastní rukou.
![]()
Válec 9.
Čela tohoto válečku jsou začerněna a je nutné do něj pohlédnout. Pak s překvapením zjistíme, že místo jednoho otvoru vidíme v průhledu tři i více otvorů. Vtip je ve dvou rovnoběžných rovinných zrcadlech uvnitř a je úspěchem žáků, když toto vysloví dříve, než váleček rozeberou.
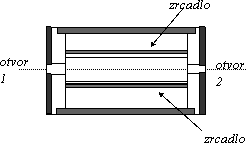
Válec 10.
Válečkem lze pohlédnout na okolní předměty, jen ubylo trochu jasu. Čelo válečku lze ale otáčet a pak se projeví něco nového: dvakrát za 360° obraz ztmavne do modra a dvakrát se opět rozjasní. Čela lze vyjmout a je na nich nalepena našedlá fólie. Fyzik ví, že jde o polarizační fólii a tu lze získat zdarma z LCD displejů vadných kalkulátorů a jiných zařízení, která jako neopravitelná končí svůj život. Tady jsou fólie příjemným zpestřením vyučování fyzice.