Souhrnný sborník Veletrhu nápadů učitelů fyziky

O příspěvku

PDF ke staženíEnglish translation

Koupil J., Vícha V.

Abstrakt

Článek popisuje sérii záběrů, které jsme natočili cenově dostupnou rychloběžnou kamerou, a komentuje jejich použití pro motivaci studentů, studium průběhu fyzikálních dějů a měření ve školské fyzice.

Rychloběžné video

Možnost zaznamenat videozáznam zpomaleně nám dává šanci studovat rychlé fyzikální děje, jako jsou hoření, výbuchy, mechanické děje, jako odtržení kapky, a podobně. Před velmi nedávnou dobou byla taková měření velmi nákladnou záležitostí, ale pokles cen digitální techniky snížil cenu kamery natolik, že je dnes relativně běžně dostupná.

My jsme pracovali s digitálním fotoaparátem Casio Exilim EX-F1, který mimo jiné nabízí možnost natáčet rychloběžné video s frekvencí 1200 FPS (snímků za sekundu) v rozlišení 336×96 bodů. (Kalibrační měření ukazuje frekvenci 1194 FPS.) Videa natočená tímto fotoaparátem jsou standardně přehrávána při rychlosti 30 FPS, tedy 40× zpomaleně.

Klipy použité v tomto článku byly zpracovávány za pomoci programu MPEG Streamclip [1] (ořezy, rotace videa), měření byla vyhodnocována za použití programu Tracker [2].

Natočená videa

Natočené klipy mají ve škole řadu použití – jednak motivační, protože překvapivé nebo fascinující video, třeba odtrhávajících se vodních kapek, dokáže povzbudit zájem o to „jak to funguje?“ (a o co jiného vlastně ve fyzice jde, že…), dále kvalitativní výzkum, tedy opravdové studium fyzikálních dějů na zpomaleném záznamu, a konečně samozřejmě videoměření – skutečné kvantitativní vyhodnocení děje na videozáznamu. Řadu klipů lze použít všemi způsoby: Například start raketky na lihový pohon [3] je strhujícím videem sám o sobě, vybízí k diskuzi o hoření par lihu uvnitř a o tom, co je to vlastně výbuch, a nakonec směřuje k měření zrychlení rakety (např. 13 g, každé měření je jiné) a rychlosti hoření par lihu.

Všechna videa zmíněná v tomto textu nebo v prezentaci na konferenci jsou dostupná z webových stránek http://kdf.mff.cuni.cz/~koupil [4], stejně jako slidy z prezentace včetně grafů a simulací. Zmiňme zde alespoň některé z natočených klipů a rozeberme je podrobně.

Povrchové napětí

Na snímku vidíme stav těsně před tím, než se vodní kapička odtrhne od vodovodního kohoutku (CIMG1258.mov).

Ze znalosti průměru kohoutku lze určit průměr krčku d₁ = 0,8 mm a průměr kapičky d₂ = 6,6 mm (kapičku budeme považovat za kouli). Kapička se odtrhává v okamžiku, kdy tíhová síla působící na kapičku bude větší, respektive rovna síle povrchové.

\[ m \cdot g \geq \sigma \cdot l \]

\[ \frac{\pi d_2^3}{6} \cdot \rho \cdot g \geq \sigma \cdot \pi d_1^2 \]

\[ \sigma \geq 0,059 \mathrm{N \cdot m^{-1}} \]

Relativní odchylka od tabulkové hodnoty činí 20 %. Odchylka je způsobena především chybou v určení veličin d₁ a d₂ – velikosti pixelů.

Vodní kladivo

Zazátkovanou láhev z části naplněnou vodou uchopíme rukavicí za hrdlo a připravíme si paličku k úderu (viz [5]).

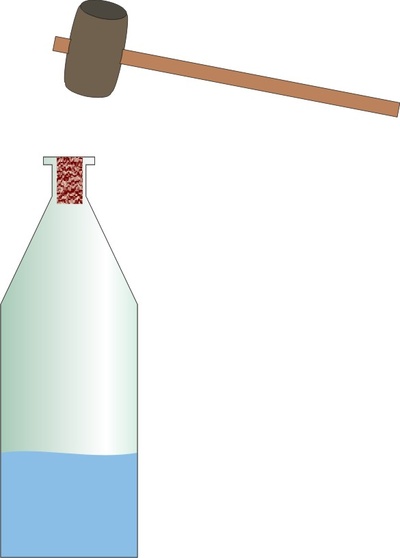
Necháváme studenty hádat, která z možností po nárazu paličky nastane:

a) Láhvi se nic nestane.

b) Láhvi se utrhne dno.

c) Láhvi se utrhne hrdlo.

d) Zátka ve zpětném rázu vyskočí ven.

Nastane možnost b), jaké je ale správné vysvětlení?

Je zřejmé, že po nárazu paličky se lahev pohne se zrychlením dolů a setrvačnost vody způsobí její zpoždění proti dnu.

Co odhalila rychloběžná kamera (CIMG1247.mov)?

Při krokování snímků se přibližně na pět milisekund objeví u dna průsvitné „bublinky“ (na obrázku), které rychle zanikají, a následně se dno utrhne.

Domníváme se, že po úderu dojde u dna ke snížení tlaku a následnému jevu kavitace. Jde o vznik bublin vakua, resp. vodních par nízkého tlaku, které rychle implozí zanikají. Při implozi vznikají rázové vlny, které urazí dno. Podobné rázové vlny dokážou narušovat i ocelové lopatky turbín či čerpadel.

Pružný odraz míčku

Odraz míčku je zaznamenán v souboru CIMG1231.mov. Míček má průměr d = 24 mm a hmotnost m = 8,0 g.

Videozáznam umožňuje určit řadu veličin.

a) Okamžitou rychlost dopadu.

Krokováním po snímcích určíme, že míček se posune o svůj průměr d za čas t₁ = 0,023 s. Průměrnou rychlost míčku vypočítáme \( v_1 = \frac{d}{t_1} = 1,04\,\mathrm{m\,s^{-1}}\). Čas t₁ je velmi krátký, proto lze průměrnou rychlost považovat za rychlost okamžitou.

b) Z jaké výšky h₁ míček padal?

Ze zákona zachování mechanické energie plyne \( h_1 = \frac{v_1^2}{2g} = 0,055\,\mathrm{m}\).

c) Jakou rychlostí v₂ se míček odrazil a do jaké výšky h₂ vystoupil?

Podobně jako v úkolu a) určíme t₂ = 0,028 s, rychlost odrazu \( v_2 = \frac{d}{t_2} = 0,86\,\mathrm{m\,s^{-1}}\), výška výstupu \( h_2 = \frac{v_2^2}{2g} = 0,038\,\mathrm{m}\).

d) Jakou silou působil míček na podložku?

Sílu vypočítáme ze změny hybnosti míčku a doby vzájemného působení mezi míčkem a podložkou. Krokováním videozáznamu určíme, že míček je v kontaktu s podložkou v průběhu 3 snímků, což znamená Δt = 0,0025 s. \[ F = \frac{m(v_1+v_2)}{\Delta t}\] \[ F = 6,1\,\mathrm{N}\]

Jde o sílu, kterou působila podložka na míček. Podle zákona akce a reakce působil míček na podložku stejně velkou silou opačného směru.

e) Jak velký byl průměrný tlak na podložku?

Pro výpočet tlaku je třeba z videozáznamu určit plochu, na kterou míček působil. Jedná se o kruh, který má maximální průměr d₁ = 7,8 mm. Podle vztahu \(p=\frac{F}{S} \)  vychází, že průměrný tlak byl větší než 128 kPa.

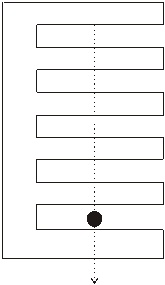
Volný pád „hřebene“

Volný pád hřebene s pukem je zaznamenán v souboru CIMG1448.mov. Pro videozáznam bylo zvoleno těleso tvaru hřebene, které slouží k snímání volného pádu optickou závorou systému ISES (viz [6]). Šířka zubů i mezer je 1 cm, a tak lze krokováním videozáznamu sestavit graf: Závislost polohy na čase. V Excelu proložíme regresní polynomickou funkci a získáme tíhové zrychlení.

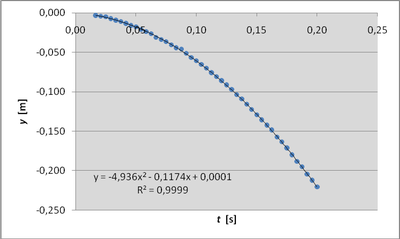
Tíhové zrychlení v tomto případě vychází g = 9,87 m·s^-2. Při pádu samotného hřebene a pádu hřebene zatíženého pukem vychází podobné hodnoty, čímž dokazujeme, že zrychlení volného pádu (pokud lze zanedbat odpor vzduchu) nezávisí na hmotnosti tělesa. Pokud jsme ale zatížili hřeben váčkem s pískem, zrychlení se výrazně změnilo, např. g = 9,34 m·s^-2. Proč?

Videozáznam CIMG1446_1.mov poskytuje vysvětlení. Váček je z pružné látky, která je v klidovém stavu předpjatá tíhou písku jako pružina. Při uvolnění hřebene i váčku obě tělesa padají a těžký váček strhává v prvních okamžicích lehký hřeben k sobě.

Stav beztíže

Předchozí úloha nás inspirovala k natočení videozáznamu CIMG1262.mov. Dvě závaží stejné hmotnosti jsou spojena pružinou. Horní závaží držíme v ruce a pak uvolníme. Na videozáznamu pozorujeme, jak horní závaží zrychluje směrem dolů a dolní závaží v prostoru „visí“.

Před uvolněním působí na horní závaží tíhová síla m·g směrem dolů a stejně velkou silou m·g musí působit ruka směrem vzhůru. Na dolní závaží v klidu působí směrem dolů také síla m·g a směrem vzhůru na něj působí horní závaží silou m·g.

Po uvolnění působí na horní i dolní závaží tíhová síla m·g směrem dolů a zároveň na sebe stále působí obě závaží akcí a reakcí. Bezprostředně po uvolnění mají akce a reakce velikost opět m·g, se zkracováním pružiny velikosti sil klesají. Dolní závaží tedy zůstává chvíli na místě a horní závaží zrychluje se zrychlením větším než g.

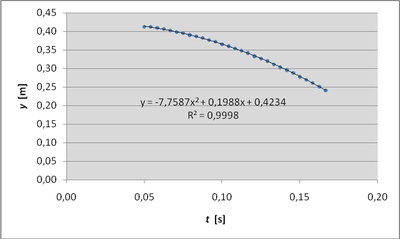
Metodou kvadratické regrese vychází pro horní závaží zrychlení g = 15,52 m·s^-2.

Překvapivě vysoký výskok

Do gumového míčku (hopíku) o hmotnosti m1 = 24,3 g a průměru 34 mm je zavrtán drát, na kterém je navlečený pingpongový míček o hmotnosti m2 = 1,7 g a průměru 37 mm.

Dopad této dvojice míčků na podložku zachycuje videozáznam CIMG1242.mov. Po dopadu pingpongový míček vyskočí do větší výšky, než ze které padal. Platí zákon zachování energie?

Videozáznam prozrazuje, že v průběhu pádu se vlivem proudění vzduchu dvojice míčků od sebe oddělí (mezera je asi 6 mm). Hopík pak dopadá dříve a odráží se proti pohybu pingpongového míčku.

Úlohu lze řešit jako centrální ráz dvou pružných koulí. Z videozáznamu jsme určili rychlosti míčků před vzájemnou srážkou v₁ = 1,68 m·s^-1, v₂ = 2,76 m·s^-1. Pokud by šlo o dokonale pružnou srážku, počítala by se rychlost u₂ pingpongového míčku po srážce: \[u_2 \frac{2 m_1 v_1 - m_2 v_2+m_1 v_2}{m_1 + m_2}\]

Vychází teoretická hodnota u₂ = 5,54 m·s^-1. Měřením rychlosti z videozáznamu vychází hodnota u₂ = 6,05 m·s^-1, relativní odchylka je 9 %. Vzhledem k tomu, že ráz nemůže být ideálně pružný, očekávali bychom spíše, že teoretická hodnota rychlosti bude vyšší. Naměřené výsledky si vysvětlujeme jednak nepřesností měření rychlosti na obrázku s nízkým množstvím pixelů, jednak aerodynamikou objektu o nízké hmotnosti, který prudce obrátí směr pohybu, nicméně tuto hypotézu jsme nijak netestovali.

Stav beztíže v lahvi

Do plastové lahve jsme udělali několik otvorů a naplnili vodou. Pokud držíme lahev v ruce, voda stříká ze všech otvorů, přičemž největší rychlost je v otvoru, který je nejhlouběji pod hladinou. Tento experiment vychází z článku Adriana Corony a kol. [7].

Jakmile lahev uvolníme a necháme padat volným pádem, vytékání z otvorů ustane. (soubor CIMG1407.mov).

Vytékání je způsobeno hydrostatickým tlakem, pro který platí ph = h·ρ·g. Při pádu padá lahev i voda se stejným zrychlením g, obě tělesa jsou ve stavu beztíže a voda nevyvolává žádný tlak na stěny nádoby. V této soustavě vymizí hydrostatický tlak.

Literatura a odkazy:

[1] MPEG Streamclip, URL: <http://www.squared5.com/> [cit. 30. 9. 2010]

[2] Tracker, URL: <http://www.cabrillo.edu/~dbrown/tracker/> [cit. 30. 9. 2010]

[3] Z. Polák: Jednoduché pokusy, Veletrh nápadů učitelů fyziky 7, Praha 2002

[4] J. Koupil, osobní stránky <http://kdf.mff.cuni.cz/~koupil/pocitace/rychlobezka.php> [cit. 30. 9. 2010]

[5] A. Caletka: Dva pokusy, Veletrh nápadů učitelů fyziky 1, Praha 1996

[6] V. Vícha: Ukázka laboratorních prací měřených soupravou ISES, Veletrh nápadů učitelů fyziky 7, Praha 2002

[7] Adrian Corona et al 2006 Phys. Educ. 41 208, doi: 10.1088/0031-9120/41/3/F05