O příspěvku
PDF ke staženíInovace výuky fyziky na základní škole a gymnáziu
Abstrakt
In the article two themes from the kinematics and the hydromechanics are mentioned. The aim of the work is to increase the interest of pupils for physics at primary and grammer school.
Úvod
Skutečnost, že tento veletrh je už devátý, svědčí o tom, že jde o semináře životaschopné a užitečné. Jejich cílem je zlepšit fyzikální vzdělávání na všech typech škol. Ve svém příspěvku chci uvést několik myšlenek a námětů, které podle mých zkušeností mohou přispět ke zlepšení fyzikálního vzdělávání žáků a studentů (v dalším jen „žáci“) základních škol a gymnázií, kteří se většinou nebudou v životě fyzikou živit a mají k ní vesměs negativní vztah. Po absolvování vysoké školy jsem učil fyzice 7 let na jedenáctileté střední škole a nyní externě 6 let na gymnáziu.
I když se obsah fyziky v současné škole výrazně neliší od obsahu téměř před 50 lety, nemá výuka fyzice šanci na úspěch, probíhá-li stejným způsobem jako tenkrát. Je tomu tak hlavně proto, že:
• „Startovní čára“ dnešních žáků je značně odlišná od těch před 50 lety (nebyla televize, mobily, CD, výpočetní technika, Internet aj., které jsou pro dnešní generaci samozřejmost). Tenkrát byla škola hlavním zdrojem informací, dnes jsou to multimédia, výpočetní technika a zejména Internet.
• Obsah fyziky, zahrnující hlavně klasickou fyziku, nekoresponduje s jejich vnímáním světa. Připadá jim archaický, nesoučasný a vnitřně je nemotivuje. Například určování hmotnosti těles vážením a digitální „váhy“, které udávají nejen hmotnost zboží, ale současně cenu.
• Současná výuka fyziky (nejen fyziky) tuto skutečnost málo respektuje a důsledkem toho žáci nepociťují potřebu se jí učit a investují čas i duševní úsilí na studium jiných předmětů, pro ně méně náročných. Co však akceptují, co je motivuje a přispívá k většímu zájmu o fyziku, je spojování učiva s jeho využitím v praxi.
V dalším uvedu dva náměty inovace výuky kinematiky a hydromechaniky, při které lze využít jednoduché pomůcky nevyžadující téměř žádné finanční prostředky. Přitom žáci získávají nejen fyzikální poznatky, ale ještě něco „navíc“ co přispívá k utváření jejich osobnosti obecně.
1. Úvod do kinematiky
Tradiční postup
Vysvětlení pojmu pohyb jako změna polohy tělesa, relativnost klidu a pohybu, klasifikace pohybů, dráha a rychlost.
Inovace
K základním kinematickým pojmům: trajektorie a dráha pohybu tělesa (hmotného bodu=těžiště), vztažná soustava, relativnost klidu a pohybu, lze dospět při vyhodnocení jednoduchých pokusů s jízdním kolem, na jehož obvodu je upevněna žárovka z kapesní svítilny, připojená k ploché baterii (stačí výrazně vyznačit sledovaný bod např. svítící barvou nebo uvázáním barevné stužky). Místo kola můžeme použít kuličku upevněnou na motouzu.
Za vhodný považuji následující postup:
1. Na tabuli nakreslíme křídou čáru (trajektorii).
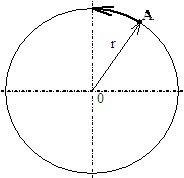
2. Dvojice žáků rozestavíme okolo stolu tak, aby mohli pozorovat pohyb svítící žárovky z různých míst ve třídě. Požádáme je, aby sdělili a na tabuli zakreslili trajektorii pohybující se žárovky (při opakovaném pokusu případně určili i velikost dráhy žárovky). Záznam pozorování, který bude na tabuli ukazuje obr. 1.
3. Ptáme se, kdo má pravdu, když o téže skutečnosti (žárovka koná pohyb po kružnici) máme pět různých tvrzení? Z diskuse vyplyne, že záleží na „vztažné soustavě“ ze které skutečnost pozorujeme. Při pozorování nás naše smysly mohou klamat. Ne však fyziku, která hledá pravdu a studuje jevy v prostoru a čase ve vztažné soustavě spojené se Zemí.
4. Kromě toho, že si žáci osvojují fyzikální poznatky (pohyb, trajektorie, vztažná soustava), získávají ještě něco „navíc“, co má obecnou platnost a přispívá k formování jejich osobnosti. Je to poznatek, že zrak nám nemusí podávat objektivní informace o pozorované skutečnosti, a proto je nutné zvažovat názor druhého člověka s kterým komunikuji a neukvapovat se ve svých úsudcích.
Pro zdůraznění této životní zásady je dobré provést pokus s válcem a dvojkuželem na nakloněné rovině, která má tvar písmene V. Postupně pouštíme po nakloněné rovině válec a dvojkužel. Paradoxně se dvojkužel pohybuje po nakloněné rovině vzhůru. Opakováním pokusu, při kterém sledujeme pohyb těžiště obou těles (stačí napnout ve vodorovném směru motouz před pohybující se osu dvojkužele), zjistíme, že se těžiště obou těles pohybují dolů tak dlouho, až zaujmou polohu s nejmenší polohovou energií.
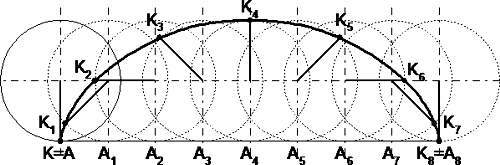
Pokus s žárovkou na obvodu kola můžeme rozšířit na pozorování trajektorie žárovky a osy kola při pohybu po vodorovném stole (nebo po podlaze). Trajektorií žárovky je cykloida, trajektorií osy je úsečka - viz obr.2. Záznam cykloidy můžeme snadno pořídit, přiložíme-li za otáčející se kolo desku s pruhem papíru a na něm postupně zaznamenáváme polohu žárovky. Použitím svítící žárovky upevněné na ráfku kola v zatemněné místnosti jsou pokusy efektnější.
| Skupina žáků |
Stanoviště žáků |
Pozorovaný průmět trajektorie |
Délka průmětu dráhy | |
| 1. |
z pohledu kolmo na rovinu kola zezadu |
|
kružnice |
2 π r |
| 2. |
z pohledu kolmo |
|
kružnice (pravotočivá) |
2 π r |
| 3. |
z levé i z pravé strany v rovině kola |
|
úsečka |
2 r |
| 4. |
z nadhledu |
|
elipsa |
2 r< s < 2 π r |
| 5. |
z nadhledu před kolem |
|
elipsa |
2 r < s <2 π r |
Obr. 1
Obr. 2
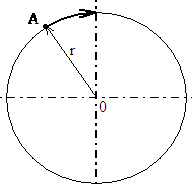
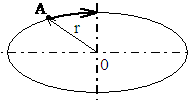
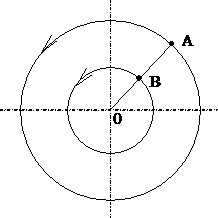
Po zavedení pojmu rychlost tělesa můžeme kola s žárovkou využít k rozšíření o pojmy rychlost posuvného pohybu a rychlost úhlová, a to i přesto, že se na ZŠ nepoužívá. Asi v polovině výpletu (drátu) spojujícího bod A a osu otáčení O umístíme druhou žárovku (barevnou) – viz obr.3 a diskutujeme se žáky otázku, která žárovka se pohybuje rychleji, když vidí, že při otočení kola se za stejnou dobu vrátily na svá místa.
Porovnáním drah a rychlosti bodů A, B při otočení kola zjistíme, že oba body jsou na původních místech, ačkoliv se po stejnou dobu bod A pohyboval po delším oblouku než bod B.
Obr. 3
2. Archimédův zákon
– úvodní hodina
Tradiční postup
Zápis na tabuli „Archimédův zákon“
Informace „Dnes se naučíme…. Objasníme….“
Řada pokusů, příp. historie objevu
Tento způsob žáky málo motivuje, předem jim sdělujeme co mají očekávat, ochuzujeme je o pocit objevování souvislostí a formulování závěrů jimi samotnými.
Inovace
Potřebné pomůcky:
• PET láhev 0,5 litru naplněná vodou tak, aby celková
- hmotnost byla 0,5 kg (gravitační síla 5 N), na láhvi
- nalepený proužek se stupnicí.
• Stojan a na něm upevněný siloměr s rozsahem 5 N(10 N).
• PET láhev 2 litrová s uříznutým hrdlem (jako kádinka).
1. fáze
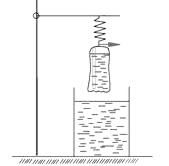
P0 Rukou napneme siloměr ve vodorovném směru tak, aby ukazoval 5 N. Otázka: Co ukazuje siloměr? (Tahovou sílu Ft, která kompenzuje opačným směrem působící svalovou sílu Fsve vodorovném směru.)
![]()
P1 Pozornost zaměříme na těleso (ne na siloměr, protože Archimédův zákon se netýká siloměru, ale tělesa). Těleso zavěsíme na siloměr a ptáme se, co siloměr ukazuje nyní? Nejčastější odpověď žáků bývá, že ukazuje gravitační sílu Fg = mg. Tato odpověď brání pochopit správně Archimédův zákon. Proto provedeme znovu pokus P0 a přivedeme žáky k závěru, že siloměr ukazuje tahovou sílu F1 = 5 N, která je v rovnováze se silou gravitační. Obě působí na totéž těleso (graficky znázorníme)
F1 = Fg
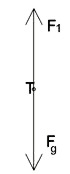
P2 Těleso postupně ponořujeme do kapaliny (zvedáme nádobu s vodou) a sledujeme, že se velikost tahové síly postupně zmenšuje. Z diskuse vyplyne závěr, že
F2 < Fg
Proto těleso ponořené do vody je nadlehčováno vztlakovou silou Fvz, která míří proti síle gravitační.
![]()
P3Opakujeme P2, ale těleso vytahujeme z vody (opačný postup). Vyslovíme závěr, že Fvz závisí na objemu ponořené části tělesa.
2. fáze
Opakujeme předchozí pokusy, ale zapisujeme číselné hodnoty, které porovnáváme. Vyslovíme závěr: Vztlaková síla je přímo úměrná objemu ponořené části tělesa.
3. fáze
Provedeme tytéž pokusy, ale s lihem (glycerinem). Vyslovíme závěr: Vztlaková síla je přímo úměrná hustotě kapaliny.
4. fáze:
Zobecníme získané poznatky a matematicky vyjádříme vztlakovou sílu
Fvz = V·ρk·g.
Teprve nyní zapíšeme téma hodiny: Archimédův zákon, sdělíme historii objevu, nebo zadáme to jako referát.
5. fáze
Zadáme problémovou úlohu: Odhadněte a potom dokažte, jak velikou silou udržíte kamaráda neplavce nad vodou, aby se neutopil? (PET láhev s vodou má přibližně stejnou hustotu jako člověk, proto je tahová síla téměř nulová, toto zjištění bývá pro žáky překvapující.)
Literatura
[1] JANÁS, J., TRNA,J. Konkrétní didaktika fyziky I. Brno: MU, 1995.
[2] JANÁS, J., MACHOVÁ, M. Jízdní kolo ve vyučování fyzice I. In Školská fyzika, 1997, 59-65.