O příspěvku
PDF ke staženíKmity a vlnění
1. Kmity na vzduchovém sloupci
K tomuto účelu je použita nádoba s obsahem přibližně V0 = 2 l, která je spojena s plastovou trubicí. Do horního otvoru trubice je vložen váleček, který má průměr stejný jako vnitřní průměr trubice. Po vložení začne váleček konat v trubici kmitavý pohyb na vzduchovém sloupci. Vzduch v nádobě a trubici je přitom stlačován a následně expandován. Posune-li se váleček v trubici o interval Δy, změní se objem o ΔV = S Δy, kde S představuje průřez trubice. S tím je spojena změna tlaku p0 v soustavě o Δp.
![]() .
.
Změna tlaku v soustavě je
![]() .
.
Násobí-li se tato změna tlaku průřezem trubice, získáme sílu, kterou stlačený vzduch působí na váleček
![]() .
.
Použitím druhého pohybového zákona obdržíme diferenciální rovnici kmitavého pohybu válečku
![]() .
.
Z pohybové rovnice (1,4) určíme periodu kmitu T válečku
![]() .
.
Tlak vzduchu p0 v klidové poloze válečku se skládá z barometrického tlaku b a korekčního tlaku pk, který je způsoben tíhou válečku: p0 = b + pk.
Provedení experimentu
K experimentu je použita plastová trubice dlouhá 1 m s průměrem 1,2 cm (Obr.1.2.). Trubice je na jednom konci nasazena do uzávěru od PET lahve. Pomocí tohoto uzávěru je možno trubici upevnit na libovolnou láhev s odpovídajícím závitem. V experimentu použité lahve měly objem 1,5 až 2 l. Do trubice je vkládán kovový váleček s magnetkou. Hmotnost válečku je možno zvýšit připevněním dalšího menšího válečku. Na trubici je měděným drátem navinuto celkem dvacet cívek s jednotlivým odstupem 5 cm. Konce vodiče jsou vyvedeny a připojeny na modul voltmetru systému ISES. Pro umožnění měření změny tlaku je láhev opatřena výstupem s hadičkou, která je připojena do modulu manometru systému ISES. Po aktivování měřícího systému je do horního konce trubice vložen váleček opatřený magnetkou. Váleček začne konat kmitavý pohyb. Při průchodu magnetky středem cívky je v cívce indukováno napětí úměrné rychlosti pohybu válečku s magnetkou. Napětí indukované v jednotlivých cívkách je zaznamenáváno měřícím systémem stejně jako změna tlaku. Systém ISES vytvoří grafy závislosti napětí a tlaku na čase (Obr. 1.1.)
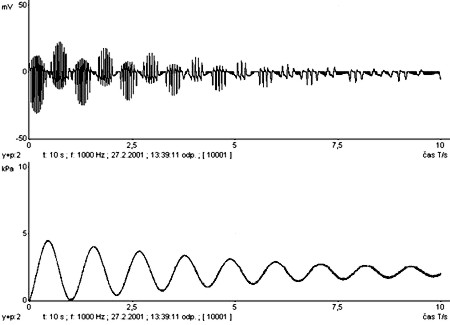
Obr. 1.1.
Ke zjištění amplitudy z grafu závislosti napětí na čase je třeba si uvědomit, že jednotlivá napěťová maxima představují průchod válečku středem cívky a jednotlivé „klubko“ představuje polovinu kmitu válečku v trubici. Proto amplituda je rovna polovině počtu zaregistrovaných cívek násobených vzdáleností mezi jednotlivými cívkami.
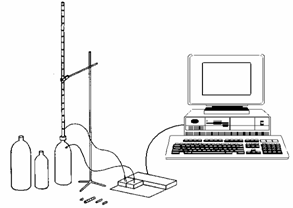
Obr. 1.2.
2. Kmity zkumavky v kapalině
Po vložení zatížené zkumavky do nádoby s kapalinou začne zkumavka konat tlumený kmitavý pohyb. Po ustálení nastane rovnováha mezi vztlakovou a tíhovou silou působící na zkumavku. Na zkumavku pak působí vztlaková síla, kterou můžeme zapsat
![]() ,
,
kde g je tíhové zrychlení, ρ hustotu kapaliny y hloubku ponoru a S průřez zkumavky.
Tuto rovnici uvedeme na standardní tvar pohybové rovnice
![]() .
.
Úhlová frekvence kmitů zkumavky je tedy
![]() .
.
3. Kmity kapaliny v U-trubici
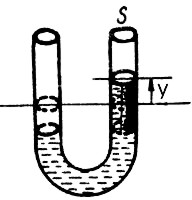
Obr. 3.1
V trubici tvaru U o průřezu S je kapalina, jejíž sloupec má délku l. Síla způsobující pohyb sloupce kapaliny je
![]() ,
,
kde y představuje výchylku hladiny vůči rovnovážné poloze a ρ hustotu kapaliny.
Rovnici zapíšeme ve tvaru
![]() .
.
Diferenciální rovnice pohybu kapaliny v trubici je
![]() .
.
Úhlová frekvence kmitů kapaliny v trubici je tedy
![]() .
.
Perioda kmitů kapaliny v trubici je
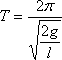 .
.
4. Kmity tělesa na struně
Na vlákně o délce l je uprostřed umístěno tělísko o hmotnosti m. Vlákno je jedním koncem připevněno k pevné stěně a druhý konec je napínán přes kladku konstantní silou P, kterou způsobuje hmotnost závaží (obr. 4.1). Následně určíme periodu vlastních kmitů T vlákna, jestliže vlákno vychýlíme o malou délku. Hmotnost vlákna lze zanedbat.
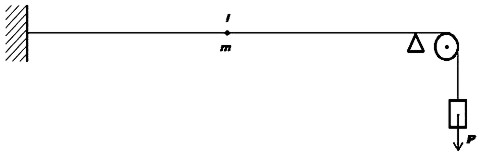
Obr. 4.1
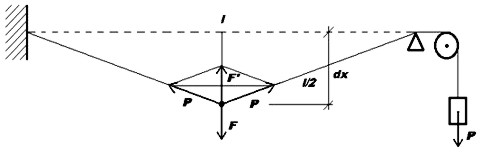
Obr. 4.2
Nejprve vypočítáme funkční závislost velikost síly F na malé výchylce y:
Z podobnosti trojúhelníků na obr. 4.2 plyne vztah ![]() . Odtud
. Odtud ![]() .
.
Porovnáním ze vztahem F = -ky dostáváme ![]() .
.
Dosazením do vztahu pro úhlovou frekvenci harmonického oscilátoru ![]() získáme periodu vlastních kmitů tělesa na struně:
získáme periodu vlastních kmitů tělesa na struně: ![]()
5. Demonstrace Dopplerova jevu.
Pohár (dutá kovová koule se seříznutým vrchlíkem) vyvážený symetricky k ose protizávažím (viz obr. 5.1) upevníme v ose do držáku odstředivého stroje. Po roztočení odstředivého stroje vzniká tření vzduchu o hranu vrchlíku tón a frekvenci f.
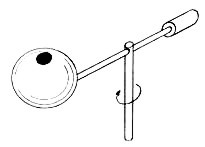
Obr. 5.1
Pozorovatel pak slyší zázněje vznikající složením tónů, které vnímá při přibližování a vzdalování poháru. Vlastní provedení experimentu je zřejmé z obr. 5.2.
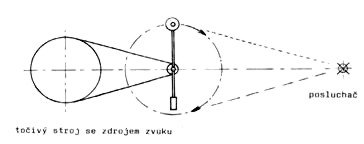
Obr. 5.2
Poznámka: Zajímavé je, že výška tónu se v tomto případě nemění spojitě s rostoucími otáčkami, ale skokem. Totiž při proudění vzduchu štěrbinou (jejíž jedna hrana je ostrá) vzniká při určité rychlosti kolem ostří hrany turbulentní proudění a po obou stranách otvoru, vně i uvnitř, se vytvářejí v pravidelných sledech víry (obr. 5.3). Podobné periodicky se opakující víry (Carriérovy víry) vznikají nejen při průchodu úzkou štěrbinou, ale i při nárazu proudícího vzduchu na ostrou hranu, při prudkém mávnutí holí nebo bičem, při pohybu vzdušných proudů kolem drátů a strun při větru (tzv. Eolova harfa) a také při proudění vzduchu kolem ostré hrany seříznutého vrchlíku poháru (dutá koule zde působí jako rezonátor). Takto vznikající tóny jsou slabé intenzity, pokud nejsou zesíleny rezonancí vzduchového sloupce, napojeného k tomuto oscilátoru. Jejich stálá frekvence se udržuje i při dosti značném kolísání tlaku vzduchu. Přesáhne-li však tlak určitou mezní hodnotu, rozpadne se vír ve dva, kmitočet takového „třecího“ tónu se zdvojnásobí - nastane „přefouknutí“ do 2. harmonického tónu. Při dalším stupňování tlaku se může vír rozpadnout na tři samostatné víry („přefouknutí“ do 3. harmonického tónu). Tyto jevy byly poprvé zkoumány a popsány českým fyzikem Čeňkem Strouhalem r. 1878.

Obr. 5.3
Tvoří-li se výše popsané třecí tóny při průchodu úzkou štěrbinou o šířce u a vzduch proudí rychlostí v, je frekvence vírů f určena vztahem
![]() .
.
6. Rezonance
Reproduktor připojíme k tónovému generátoru (viz obr. 6.1) Při určité frekvenci (či jejím násobku) rezonuje vždy určitý ocelový pásek upevněný nad reproduktorem; vzduchový sloupec ve svislé trubici („komínu“). Výšku vzduchového sloupce zde můžeme měnit ještě pomocí pístu.

Obr. 6.1