O příspěvku
PDF ke staženíPár zajímavých nápadů IV
Abstrakt
Příspěvek je věnován třem jednoduchým pomůckám, které si může každý učitel fyziky sám vyrobit: "Tlak plynu v balónku", "Zpívající trubky" a "Zpívající tyčky". Také v příspěvku předvedu, jak změřit časový průběh, frekvenci a rychlost zvuku s těmito pomůckami.
Tlak plynu v balónku
Pro tlak uvnitř balónku platí přibližně (v prostřední části grafu – obr. 5.) vztah \(p=\frac{k}{d}\), kde p je tlak plynu v balónku a d je průměr balónku. Tuto vlastnost je možné kvalitativně demonstrovat pomocí dvou různě nafouknutých balónků, které různě nafoukneme a navzájem propojíme.

Obr. 1 - Demonstrace různosti tlaků uvnitř balónků
Před otevřením ventilů se můžeme žáků zeptat: Co se bude dít, když otevřeme oba ventily? Většina laiků odpovídá: Větší balónek se bude zmenšovat a menší zvětšovat tak dlouho až budou stejně velké. Při otevření obou ventilů se překvapivě budou rozměry menšího balónku zmenšovat a většího zvětšovat. Tento jednoduchý pokus svědčí o tom, že tlak vzduchu uvnitř méně nafouknutého balónku je větší a tlak plynu uvnitř více nafouknutého balónku je menší.
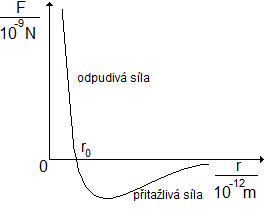
Obr. 2 - Graf závislosti velikosti síly působící mezi dvěma atomy na jejich vzdálenosti
Vysvětlení
Podle Pascalova zákona je tlak plynu v uzavřené nádobě (uvnitř obou propojených balónků) ve všech místech plynného tělesa stejný. Co způsobuje, že uvnitř menšího balónku je tlak plynu větší? Samozřejmě to způsobují přitažlivé síly mezi atomy latexu (pryž na bázi přírodního kaučuku), z něhož je balónek vyrobený. Jestliže je vzdálenost mezi atomy větší než při rovnovážné poloze r0 (před nafukováním balónku) narostou přitažlivé síly mezi částicemi kaučuku na určitou maximální hodnotu a potom při dalším nafukování se přitažlivé síly zmenšují (viz obr. 2). Tím se tlak uvnitř balónku zmenšuje nepřímo úměrně (přibližně) se zvětšujícím se průměrem d.
Výroba pomůcky
Potřebné součástky (viz obr. 3), tedy dvoucestný ventil (2 ks), plastovou hadičku, gumovou zátku (2 ks) a další spojovací součástky můžete koupit například u prodejce [1].

Obr. 3 - Potřebné součástky
Návrh měření.
Zkus změřit závislost přetlaku plynu p uvnitř balónku na průměru d balónku (viz obr. 4.).
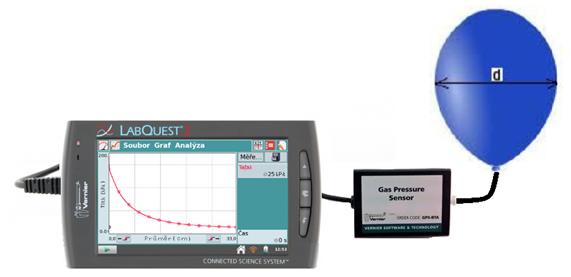
Obr. 4 - Měření závislosti přetlaku plynu na průměru balónku
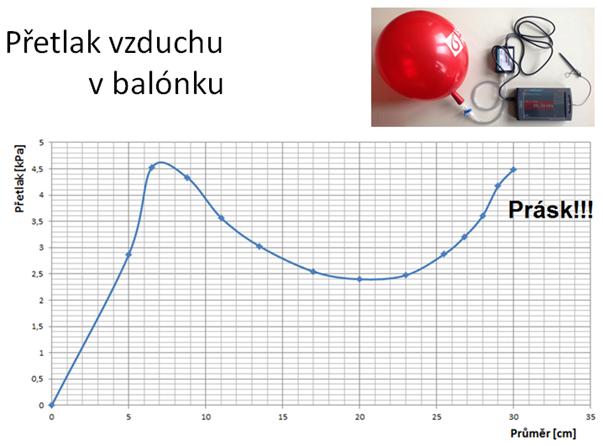
Obr. 5 - Naměřená závislost přetlaku na průměru
Zpívající trubka
Za 33 dolarů si můžete tuto pomůcku koupit u amerického prodejce školních pomůcek [2].
Jak tato pomůcka funguje? Budeme-li spodní vnitřní část trubky asi 10 sekund nahřívat podle obr. 6 plynovým kahanem, začne po oddálení kahanu trubka vydávat hlasitý tón po dobu 10 až 30 sekund. Vydávání zvuku trubkou můžeme přerušit, jestliže trubku nakloníme do vodorovné polohy. Naopak, nakloníme-li trubku zpět do svislé polohy, bude pokračovat ve vydávání zvuku. Jestliže bude mít trubka větší délku, bude vydávat nižší tón.
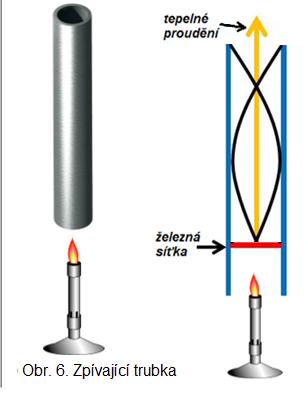
Obr. 6 - Zpívající trubka
Co je uvnitř trubky? Jak tato pomůcka funguje? U dolního konce uvnitř trubky je upevněna železná síťka. Ta se plynovým kahanem nahřeje. Tím vznikne po oddálení kahanu turbulentní proudění ohřátého vzduchu (více než 500°C) směrem vzhůru, které začne produkovat zvuk. Frekvence tónu odpovídá délce trubky od mřížky k hornímu konci. Vznik zvuku je podobný vzniku zvuku při provozu varhan.
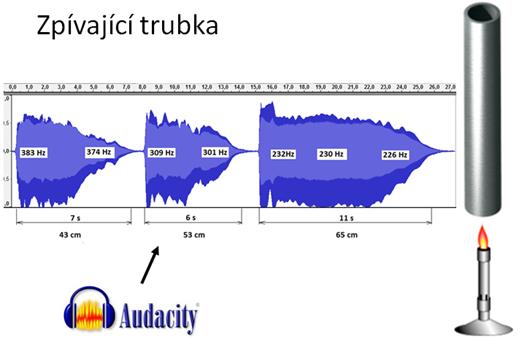
Obr. 7 - Naměřené tóny tří různě dlouhých „zpívajících trubek“ a jejich frekvenční analýza v programu Audacity. Uvedené délky jsou délkami od vnitřní mřížky k hornímu konci.
Z obr. 7 a uvedených frekvencí lze vypočítat rychlost zvuku (přibližně 650 m∙s-1). Z rychlosti pak lze vypočítat teplotu proudícího vzduchu (asi 520 °C).
Výroba pomůcky „Zpívající trubky“
K výrobě této pomůcky stačí kus železné trubky (trubka bezešvá hladká 44,5 x 2,6), kterou jsem koupil u prodejce železa [3] za přibližně 145,- Kč (tři kusy – 50, 60 a 75 cm dlouhé). Železnou síťku můžeme získat u učitele chemie. V chemii se používá pro plynové kahany pro rozptýlení tepla. Samozřejmě použijeme pouze samotnou síťku bez azbestu.

Obr. 8 - Železná síťka (azbestová)
Měření zvuku, který vydává „Zpívající trubka“
K měření zvuku můžeme použít obyčejný mikrofon k PC.

Obr. 9 - Mikrofon k PC
Dále použijeme freewarový program Audacity. Osobně používám verzi 1.2.6. Tuto verzi můžete zdarma stáhnout na webu [4]. Použití mikrofonu s programem Audacity podrobně popisuje Leoš Dvořák v [5].
Tento program umožňuje nahrát zvuk pomocí mikrofonu.
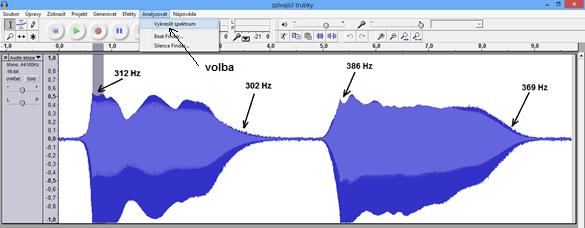
Obr. 10 - Zvuk dvou “Zpívajících trubek” 60 a 50 cm
V dalším kroku ve stejném programu můžeme provést analýzu zvuku nebo části zvuku: Označíme myší malou část záznamu zvuku a v menu zvolíme Analyzovat – Vykreslit spektrum (viz obr. 10).
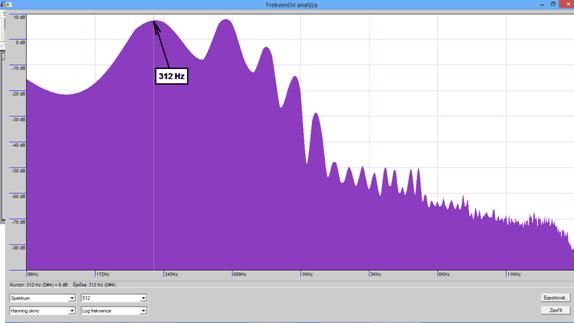
Obr. 11 - Frekvenční analýza zvuku ze “Zpívající trubky” (viz obr. 10)
Na obr. 11 můžeme vidět frekvenční analýzu záznamu začátku zvuku delší „Zpívající trubky“ (60 cm). První naměřená frekvence odpovídá základní frekvenci fz. Další maxima odpovídají vyšším harmonickým frekvencím a mají přibližně fk = k ∙ fz; k ϵ N. Z obr. 11 je také patrné, že frekvence na začátku zvuku je vyšší než na konci zvuku. Tento jev je způsoben chladnutím vzduchu, mřížky a trubky.
Zpívající tyčky
Za 50 dolarů si můžete tyto pomůcky koupit u amerického prodejce školních pomůcek [2]. Jedná se o tři kusy hliníkových tyčí o délkách 61, 76 a 91 cm. Koupil jsem si 300 cm dlouhou hliníkovou tyč o průměru 10 mm (stála 140,- Kč). Z této tyče jsem si pilkou na železo nařezal tři kusy o délkách 76, 91 a 106 cm.

Obr. 12 - Zpívající tyčky [6]
Hliníkovou tyčku upevníme uprostřed (můžeme tyčku uprostřed držet v ruce jako na obr. 12). Jestliže lehce udeříme kladívkem do konce tyčky, bude tyčka vydávat tón po dobu 30 s (i déle). Delší tyčka bude vydávat tón s nižší frekvencí.
Měření zvuku, který vydávají „Zpívající tyčky“
K měření tónů zvuků „Zpívajících tyček“ jsem použil stejně (jako výše) mikrofon a program Audacity. Stejně jako výše nahrajeme tento zvuk a provedeme jeho frekvenční analýzu (Obr. 13).
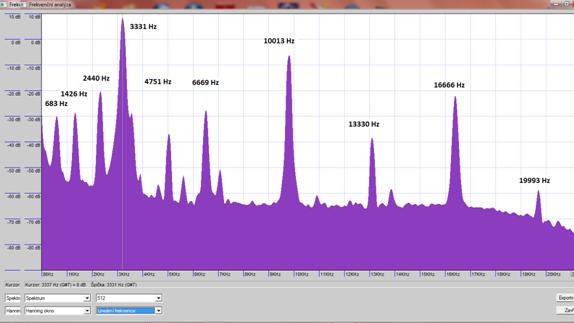
Obr. 13 - Frekvenční analýza tónu hliníkové tyčky o délce 76,1 cm a průměru 10 mm
Naměřená frekvence fz = 3331 Hz odpovídá základní frekvenci. Další maxima odpovídají vyšším harmonickým frekvencím a mají přibližně fk = k ∙ fz; k ϵ N. Ze základní frekvence můžeme vypočítat rychlost šíření zvuku v hliníku: \[ v= \lambda f = 2lf = 2 \cdot 0,76 \cdot 3331\,\mathrm{\frac{m}{s}} = 5070\,\mathrm{\frac{m}{s}} .\]
Stejné měření můžeme provést pro hliníkovou tyčku o délce 91 cm (průměr 10 mm).
Naměřená frekvence fz = 2790 Hz odpovídá základní frekvenci. Další maxima odpovídají vyšším harmonickým frekvencím a mají přibližně fk = k ∙ fz; kϵ N. Ze základní frekvence můžeme vypočítat rychlost šíření zvuku v hliníku: \[ v= \lambda f = 2lf = 2 \cdot 0,91 \cdot 2790\,\mathrm{\frac{m}{s}} = 5090\,\mathrm{\frac{m}{s}} .\]
A stejně můžeme provést měření pro hliníkovou tyčku o délce 106 cm (průměr 10 mm).
Naměřená frekvence fz = 2392 Hz odpovídá základní frekvenci. Další maxima odpovídají vyšším harmonickým frekvencím a mají přibližně fk = k ∙ fz; k ϵ N. Ze základní frekvence můžeme vypočítat rychlost šíření zvuku v hliníku: \[ v= \lambda f = 2lf = 2 \cdot 1,06 \cdot 2392\,\mathrm{\frac{m}{s}} = 5071\,\mathrm{\frac{m}{s}} .\]
Hliníkovou tyčku můžeme také upevnit v ¼ délky. Tím ji „donutíme“ kmitat „hlavně“ na frekvenci, pro kterou je délka tyče rovna vlnové délce stojatého vlnění (obr. 16).
Rychlost zvuku vypočítaná pro toto měření: \[ v= \lambda f = lf = 1,06 \cdot 4770\,\mathrm{\frac{m}{s}} = 5070\,\mathrm{\frac{m}{s}} .\]
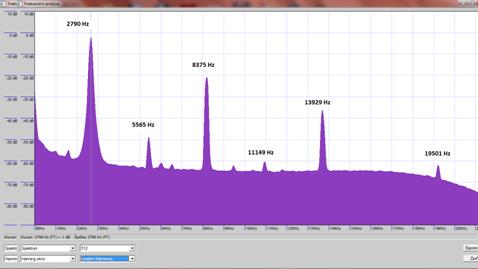
Obr. 14 - Frekvenční analýza tónu hliníkové tyčky o délce 91 cm a průměru 10 mm
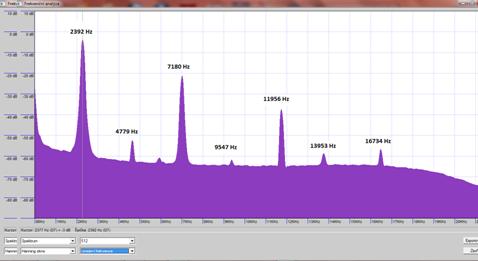
Obr. 15 - Frekvenční analýza tónu hliníkové tyčky o délce 106 cm a průměru 10 mm
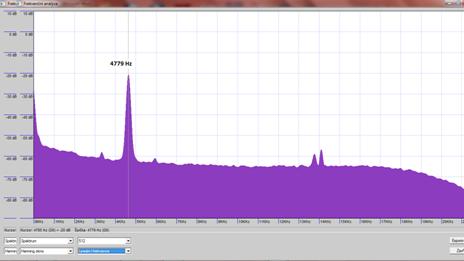
Obr. 16 - Frekvenční analýza tónu hliníkové tyčky o délce 106 cm a průměru 10 mm (upevněná v ¼ délky)
Závěr
Podle [7] pro rychlost podélné vlny v hliníkové tyči platí vztah a po dosazení můžeme vypočítat \[v= \sqrt{\frac{E}{\rho}} = \sqrt{\frac{7\cdot10^{10}}{2700}}\,\mathrm{\frac{m}{s}} = 5092\,\mathrm{\frac{m}{s}}.\] Naměřené a výše vypočítané hodnoty rychlostí vycházejí s odchylkou menší než 0,5 % vzhledem k této „tabulkové hodnotě“.
Domnívám se, že tyto jednoduché a levné pomůcky si může koupit a vyrobit každý učitel fyziky. Mohou se stát vhodným doplňkem do výuky a tak zvýšit motivaci a zájem žáků o fyziku.
Literatura
[1] www.vernier.cz
[2] http://www.teachersource.com/product/singing-pipe/sound-waves
[3] http://www.ferona.cz/cze/katalog/detail.php?id=26151
[4]http://www.stahuj.centrum.cz/multimedia/mp3_a_audio/mp3_a_audio_nastroje/audacity/verze/
[5] Dvořák L.: Pokusy se zvukovou kartou. In: Dílny Heuréky 2005. Sborník konference projektu Heuréka, Náchod, září 2005. Ed. L. Dvořák. Prometheus, Praha 2006
[6] http://www.teachersource.com/product/singing-rod/sound-waves
[7] Břetislav P., Dvořák L.: Zvuky kmitajících tyčí. Souhrnný sborník Veletrhu nápadů učitelů fyziky.