O příspěvku
PDF ke staženíJaké je maximální zrychlení osobního automobilu?
Úvod
Dle informace z médií [1] připravuje německá firma sportovní automobil, který zvýší rychlost z nuly na sto kilometrů za hodinu za méně než jednu sekundu. Fyzika hned napadne: Je to vůbec možné? Jaké jsou fyzikální limity akcelerace vozidla s poháněnými koly? Současné sportovní automobily nezrychlí z 0 na 100 km/h za méně než dvě sekundy. To dokáží jen vysokovýkonné závodní vozy se speciálními pneumatikami, viz tab. 1.
| typ vozu |
zrychlování 0-100 km/h [s] |
zrychlení [m/s-2] |
| Renault F1 |
1,7 |
16,3 |
| Bugatti Veyron |
2,46 |
11,3 |
| Porsche 911 Turbo |
2,7 |
10,3 |
| Ferrari F12 Berlinetta |
3,1 |
9,0 |
Tabulka 1
V příspěvku budou prezentovány dva různé modely výpočtu meze zrychlení. První, často prezentovaný, není fyzikálně správný, ale za jistých podmínek může být vyhovující aproximací. Diskuse výsledků druhého modelu v podstatě vyloučí, aby vozidlo s poháněnými nápravami dosáhlo tak velkého zrychlení, které výrobce očekává.
Model 1
Často najdeme následující postup řešení: Předpokládejme, že automobil má hnanou jednu nápravu (například zadní kola) a podélná poloha těžiště automobilu je uprostřed mezi nápravami. Dále zanedbejme vliv rotační hmoty kol. Model vychází z obr. 1. Ve svislém směru je tíhová síla kompenzována tlakovými silami podložky, které při zvolené poloze těžiště jsou shodné. Maximální urychlující síla je dána součinitelem smykového tření f a platí pro ni[1] \[\tag{1} F_{max} = f N_{1} = f \frac{G}{2} = f \frac{mg}{2}, \] kde m je hmotnost automobilu. Maximální zrychlení je pak rovno \[\tag{2} a_{max,1} = \frac{F_{max}}{2} = f \frac{g}{2}. \]
Dostáváme velmi jednoduchý výsledek. Je však podivné, že při výpočtu nebyl nikde použit předpoklad zadní hnané nápravy i když ze zkušenosti víme, že automobily se zadní poháněnou nápravou se stejným poměrovým zatížením náprav zrychlují na kluzkém povrchu lépe[2]. Model č. 1 tedy zrychlení automobilu nepopisuje správně.
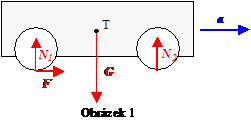
Obrazek 1
Model 2
Silový rozbor uvedený na obr. 1 je chybný. Víme, že při akceleraci se vůz pohybuje čistě translačním pohybem, nerotuje. Výsledný moment působících sil musí tedy být roven nule, což síly z obr. 1 evidentně nesplňují. Aby síly N1 a N2, kompenzovaly moment urychlující síly F (moment počítáme vzhledem k těžišti), musí mít síla N1 větší velikost než síla N2. Správný rozbor sil je na obr. 2.
Ve svislém směru vozidlo nezrychluje, pro vertikální síly tedy musí platit silová rovnováha \[\tag{3} G = N_1 + N_2. \]
Z podmínky momentové rovnováhy platí \[\tag{4} F_{max} h + N_2\frac{l}{2} = N_1\frac{l}{2}, \] kde Fmax je maximální urychlující síla, pro kterou platí \[\tag{5} F_{max} = f N_1. \]
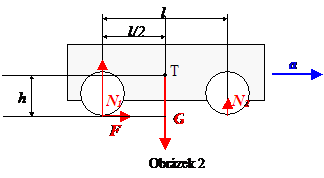
Obrazek 2
Význam ostatních symbolů je zřejmý z obr. 2. Rovnice (4), (5) a (6) tvoří soustavu o třech neznámých Fm, N1 a N2. Jejím řešením získáme \[\tag{6} a_{max,2} = f \frac{g}{2 \left( 1- \frac{hf}{l} \right)} .\]
Na jedné straně výsledek modelu 2 splnil naše očekávání: vede k vyšší hodnotě maximálního zrychlení než model č. 1. Při akceleraci jsou více zatížena zadní kola (na úkor kol předních), a proto má vůz s pohonem zadních kol výhodu. Na druhé straně však se výsledek smysluplný nezdá: s klesající výškou těžiště a rostoucím rozvorem náprav roste maximální zrychlení nade všechny meze a dokonce může nabýt i záporných hodnot!
Omezení modelu č. 2
Zrychlení automobilu by mohlo divergovat, pokud by divergovala i síla N1. Pak by ovšem síla N2 musela mířit směrem dolů, což pro jízdu automobilu není reálné. Model č. 2 tedy platí pouze za předpokladu, že N2 > 0. Při porušení této podmínky by došlo ke zvednutí předních kol vozidla.
Z rovnic (4), (5) a (6) vyjádříme vertikální složku síly N2. \[\tag{7} N_2 = \frac{mg\left( 1-\frac{2fh}{l} \right)}{2-\frac{2fh}{l}}. \] Z podmínky N2 > 0 plyne nerovnost \[\tag{8} \frac{2fh}{l} < 1. \] Za splnění této podmínky bude pro akceleraci limitující smykové tření mezi pneumatikou a vozovkou. V opačném případě akceleraci omezí zvednutí předních kol.
Omezení modelu č. 1
Srovnejme výsledky modelů 1 a 2 (rovnice (2) a (6)). Vidíme, že započtení momentové rovnováhy v modelu 2 přináší korekci rostoucí s hodnotou součinitele statického tření f. Pro dostatečně malá f by tedy i model 1 byl schopen poskytnout výsledky s přijatelnou přesností. Pro ilustraci spočítejme, za jakých podmínek by model 1 poskytl výsledky s odchylkou menší než 10 %, tedy \[\tag{9} a_{max,2} - a_{max,1} < 0,1 \cdot a_{max,2}. \]
Po dosazení z (2) a (6) a úpravě dostaneme \[\tag{10} f \cdot \frac{h}{l} < 0,1. \]
Model 1 tedy může být dobrou aproximací pro dostatečně malé hodnoty součinitele smykového tření a nízké těžiště.
Vozidlo s pohonem všech čtyř kol
Řešení maximálního zrychlení vozidla s pohonem všech kol je překvapivě jednodušší, než u vozidla s jednou hnanou nápravou. Při akceleraci sice dochází k přerozdělení tlakových sil mezi přední a zadní nápravu, ale velikost jejich součtu je vždy rovna velikosti tíhové síly. Pokud by automobil dokázal řídit trakci obou náprav tak, aby současně dosáhly meze smyku, maximální zrychlení by bylo rovno \[\tag{11} a_{max} = \frac{F_{max}}{m} = \frac{f \cdot mg}{m} = f \cdot g.\]
Shrnutí
Výsledky jsou shrnuty na obr. 3, kde je zobrazeno maximální zrychlení automobilu s pohonem zadní nápravy jako funkce poměru h/l. Jednotlivé křivky odpovídají různým součinitelům statického smykového tření (čísla uvnitř grafu). Reálné situace vymezuje pouze šrafovaná oblast, vně této oblasti se automobil převrátí. Křivka na hranici šrafované oblasti udává současně maximální zrychlení automobilu s pohonem všech kol, které nezávisí na poloze těžiště. V hustě šrafované oblasti je chyba modelu 1 menší než 10 %.
Aby automobil zrychlil z klidu na 100 km/h za 1 s, musel by mít průměrné zrychlení asi 28 m∙s-2. Tato hodnota je v grafu vyznačena tlustou vodorovnou čarou. Pro dosažení této hodnoty by koeficient smykového tření mezi pneumatikou a vozovkou musel být nejméně 3, bez ohledu na konstrukci automobilu. Obvyklé hodnoty součinitele statického smykového tření mezi pneumatikou a betonem se udávají v intervalu 0,7 – 0,8, na asfaltu je dokonce nižší. Vyšších hodnot je možné dosáhnout jen se speciálními pneumatikami případně na speciálně upraveném povrchu (závody dragsterů). Za vyšší součinitel smykového tření však platíme velmi malou životností pneumatik. Zrychlení z 0 na 100 km/h za 1 s, které německý výrobce očekává u připravovaného automobilu, je velmi pravděpodobně nereálné.
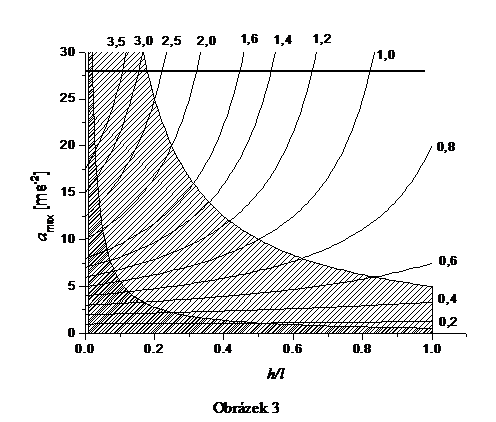
Obrazek 3
Možnosti experimentálního ověření v laboratorních podmínkách
Přímé experimentální ověření jevů při vysokém zrychlení je obtížné. Krátká doba rozjíždění a dlouhá jízdní dráha v podstatě vylučují realizaci těchto experimentů ve školních laboratorních podmínkách. Je však možné využít analogie mezi rovnoměrně zrychleným vodorovným pohybem a rovnoměrným pohybem po nakloněné rovině, viz obr. 4.
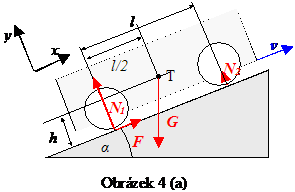
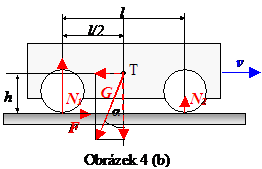
Obrazek 4 (a –vlevo, b – vpravo)
S využitím této analogie získají rovnice (3), (4) a (5) tvar \[\tag{12} mg \cos \alpha = N_1 + N_2 ,\] \[\tag{13} F_{max} h + N_2\frac{l}{2} = N_1\frac{l}{2} ,\] \[\tag{14} F_{max} = f N_1 ,\] kde navíc tahová síla motoru kompenzuje průmět tíhové síly do směru pohybu, tedy \[\tag{15} F_{max} = mg \sin \alpha .\]
Řešením soustavy rovnic dostaneme \[\tag{16} \sin \alpha = \frac{f}{f +4 \left(1- \frac{fh}{l} \right)^2 } .\]
Problém měření zrychlení tak převedeme na experimentálně mnohem jednodušší problém určení úhlu nakloněné roviny, při kterém dojde k prokluzu hnané nápravy respektive k překlopení modelu vozidla.
Literatura
[1] http://auto.idnes.cz/geniove-nebo-tluchubove-z-nuly-na-sto-pry-pod-sekundu-pda-/ak_aktual.aspx?c=A110827_202252_ak_aktual_ada
[1] Symboly pro vektorové veličiny – sílu, moment síly a zrychlení, které nejsou zvýrazněné tučným písmem označují velikosti těchto veličin a nebo složky těchto sil do vodorovného či svislého směru. Situace je vždy zřejmá z obrázku či kontextu.
[2] Podobně při zpomalení jsou účinnější kola přední nápravy, proto jsou přední brzdy více dimenzované než zadní.