O příspěvku
PDF ke staženíDrobnosti do hodin fyziky
V příspěvku jsou popsány některé jednoduché experimenty z různých oblastí fyziky, které mohou vhodným způsobem doplnit výklad. Dále je zde ukázka některých druhů testů, které lze použít pro testování žáků – jak ve fyzice, tak v matematice.
Úvod
V tomto příspěvku budou popsány experimenty a aktivity z různých oblastí fyziky a matematiky. Důvodem pro tento „mix“ je skutečnost, že to jsou, dle mého názoru, vhodné doplňky výuky, které se mi podařilo v poslední době buď vymyslet nebo předvést ve třídách během vyučovacích hodin. A vzhledem ke kladné zpětné vazbě od žáků případně od kolegů jsem se rozhodl je publikovat i v tomto sborníku.
V příspěvku budou popsány jak některé experimenty, tak některé nástroje pro testování žáků.
Experimenty
Experiment může mít ve výuce řadu funkcí (motivace, doplnění výkladu učitele, zadání problémové úlohy nebo demonstrace jejího správného řešení a podobně). Při dalším popisu experimentů naznačím, jak používám dané experimenty během výuky, ale netvrdím, že to je jediný způsob, jak daný experiment ve výuce využít.
Pítko pro ptáky
Inspirací pro výrobu pomůcky, kterou interně nazývám „pítko pro ptáky“, byla návštěva workshopu japonských kolegů na konferenci GIREP 2010 ve francouzské Remeši. Výroba pomůcky je náročnější na geometrickou představivost, ale cenově je velmi levná. Potřebujeme pouze prázdnou PET láhev s víčkem a menší plastový kelímek. V horní polovině láhve vyřízneme takový otvor, do kterého vlepíme část kelímku tak, jak je zobrazeno na obr. 1. K naplnění láhve pak budeme potřebovat kbelík, do kterého se celá láhev (včetně přilepeného kelímku) vejde. Láhev postavíme do kbelíku, přidáme do ní trošku potravinářského barviva, aby experiment lépe vynikl, a kbelík naplníme vodou. Tak se naplní obarvenou vodou i láhev; když je plná až po okraj (nebo tak, jak kbelík umožňuje), zavřeme ji víčkem (viz obr. 1). Láhev vyndáme z kbelíku a postavíme na stůl.
Nyní můžeme se žáky začít diskutovat, proč voda z kelímku přilepeného k láhvi nevyteče a kde se podobný princip uplatňuje v praxi. Žáci poměrně rychle přijdou na to, že klíčovou podmínkou stability vody v láhvi je rovnováha atmosférického tlaku vzduchu a hydrostatického tlaku vody v láhvi nad volnou hladinou vody v kelímku. Můžeme i spekulovat, jak by mohla být láhev teoreticky vysoká (resp. jaká výška vody by mohla být nad volnou hladinou vody v kelímku), aby voda ještě nevytekla.

Obr. 1. Ukázka pomůcky.
Podobný princip se používá v některých zařízeních, ze kterých pijí ptáci nebo drůbež. Tím, jak odebereme vodu z kelímku, doteče do něj další z horní části láhve. To lze i prakticky vyzkoušet.
Nafukování sáčku
Tento experiment většinou uvádím před žáky tak, že budeme soutěžit v tom, kdo na méně nádechů nafoukne cca 4 metry dlouhý igelitový sáček (jedná se vlastně o plášť válce, tj. válcový igelitový sáček bez podstav). Tento sáček lze poslepovat ze sáčků na papírové dokumenty, které lze zakoupit za několik korun v kopírovacích centrech. Důležitým předpokladem pro dosažení maximálního efektu experimentu je, aby žák-dobrovolník, který se do soutěže s učitelem přihlásí, daný experiment neznal. Zároveň je nutné žáka volit s rozmyslem tak, aby nebyl po skončení experimentu pro ostatní žáky terčem posměchu; soutěž totiž ve většině případů prohraje.
Při vlastním experimentu (resp. soutěži) se učitel a žák postaví dopředu učebny před ostatní žáky do takové vzájemné vzdálenosti od sebe, aby mezi sebou mohli držet výše popsaný igelitový sáček v téměř vodorovné poloze. První bude soutěžit žák. Cílem je, aby igelitový sáček začal nafukovat tak, jak asi napadne bez přemýšlení každého: konec sáčku zmáčkne jednou rukou k sobě, vytvoří v takto zmačkaném konci sáčku otvor a foukne (viz obr. 2). Učitel rukou pevně uzavře druhý konec sáčku a žák začne sáček nafukovat; k nafouknutí sáčku bude potřebovat přibližně 8 nádechů. Poté učitel ze sáčku vytlačí vzduch, žák jeden konec sáčku pevně stiskne a učitel začne nafukovat. Ale začne nafukovat jinak: svůj konec sáčku chytne oběma rukama a vytvoří v okraji sáčku velký otvor a ze vzdálenosti cca 10 cm do něj po předchozím silném nádechu foukne (viz obr. 3). Sáček se nafoukne tímto jedním jediným fouknutím.

Obr. 2. Nafukování sáčku na přibližně 8 nádechů.

Obr. 3. Nafukování sáčku na jeden nádech.
Vysvětlení zdánlivě zvláštního nafukování sáčku učitele využívá Bernoulliho rovnici. Ta platí v kvantitativním tvaru pouze pro ideální kapalinu, ale v kvalitativním tvaru (v místě s větší velikostí rychlosti proudící tekutiny klesá tlak) platí i pro plyny (tj. v tomto případě pro vzduch). Rychle proudící vzduch z učitelových úst strhává do sáčku i okolní vzduch (v oblasti rychle proudícího vzduchu vzniká oproti okolnímu atmosférickému tlaku podtlak). Proto lze tímto způsobem nafouknout sáček rychleji.
Hloubka ostrosti
V současné době má řada žáků či studentů ve svých mobilních zařízeních zabudován fotoaparát. Tato zařízení dokážou pořizovat velmi kvalitní snímky, ale přeci jen oproti běžným fotoaparátům mají tu nevýhodu, že vesměs není možné nastavit parametry pořizovaného snímku (čas expozice, clona, …). Proto budou standardní fotoaparáty patrně ještě dlouhou dobu sloužit pro pořizování kvalitnějších fotografií. V té souvislosti (a také vzhledem k argumentaci, jaké parametry fotografií není možné na mobilních zařízeních nastavit) je dobré, aby žáci chápali základní parametry pořizovaného snímku. Jedním z parametrů výsledné fotografie je i tzv. hloubka ostrosti. Ta určuje rozmezí vzdáleností fotografovaných předmětů od objektivu, ze kterého se předmět zobrazí na výsledné fotografii ostře. Hloubku ostrosti lze ovlivnit pomocí tzv. clonového čísla: vyšší clonové číslo (tj. menší otvor, kterým světlo vstupuje do fotoaparátu) znamená vyšší hloubku ostrosti – tj. snímek bude ostrý jako celek (viz [1]). Vyšší clonové číslo je ovšem nutné kompenzovat delší dobou expozice, takže na fotografiích s velkou hloubkou ostrosti nemohou být ostře zobrazeni např. rychle se pohybující atleti.
Jak souvisí pojem hloubka ostrosti s clonou (resp. clonovým číslem) lze ukázat dvěma způsoby. V obou z nich budeme potřebovat dataprojektor, kterým zobrazíme na promítací plochu mírně rozostřený text. V prvním případě si může každý žák zkusit experiment sám: stačí, když přimhouří oči. Tím se zúží otvor zornice (tj. na oku bude „nastavena“ větší clona) a text se zaostří. Lidé, kteří běžně používají brýle nebo kteří začínají špatně vidět, tento způsob doostřování podvědomě používají tak, že prostě mhouří oči.
Pro druhý způsob demonstrace hloubky ostrosti vystřihneme do papíru formátu A4 několik vedle sebe umístěných kruhových otvorů s průměrem od cca 1 cm do 6 cm. Před objektiv dataprojektoru, který promítá mírně rozostřený obraz, umístíme největší otvor. Přitom nepozorujeme žádné znatelné změny v promítnutém obrazu. Postupně vystřídáme všechny otvory a při použití nejmenšího z nich je jasně vidět zostření obrazu na plátně.
Fresnelova čočka a 3D displeje mobilních telefonů
Již výše jsem zmínil moderní mobilní vybavení našich žáků. Mezi různými novinkami, které jsou spíše technologického rázu (miniaturizace, vyšší výkon či paměť, …), se u řady mobilních zařízení setkáváme i se 3D displeji. Jedná se o mobilní zařízení, které musí být vybaveno též odpovídajícím softwarem, schopným zobrazovat 3D obrazy – a to jak fotografie, tak i filmy. Z fyzikálního hlediska je možné princip tohoto displeje vysvětlit a názorně ukázat pomocí tzv. Fresnelovy čočky a dětských obrázků.
Čočku, která je pojmenována po francouzském fyzikovi A. J. Fresnelovi (1788-1827), tento fyzik vynalezl v roce 1822 pro potřeby majáků na moři: zvýšila účinnost přenosu světla na moře. Fresnelovy čočky jsou (na rozdíl od klasických čoček) tenké, proto mají i menší hmotnost. Zjednodušeně lze říci, že Fresnel z klasické čočky ponechal pouze ty její části, které lámou světlo vstupující do čočky nebo z ní vystupující; ostatní její části prostě odebral (viz např. [2]). V současné době jsou tyto čočky dostupné na trhu také jako hračky nebo suvenýry v různých tvarech, takže je možné je žákům v hodinách fyziky ukázat.
Vlastnosti Fresnelovy čočky umožňují také zobrazovat 3D obrázky. Nerovný povrch čočky může zobrazovat dva různé obrazy, které pozorovatel vidí pod mírně odlišnými zornými úhly (viz obr. 4) a které až mozek vyhodnotí jako jediný obraz. Tím, že každý z obou obrazů byl pozorován pod mírně odlišnými zornými úhly, bude se výsledný obraz jevit prostorově.
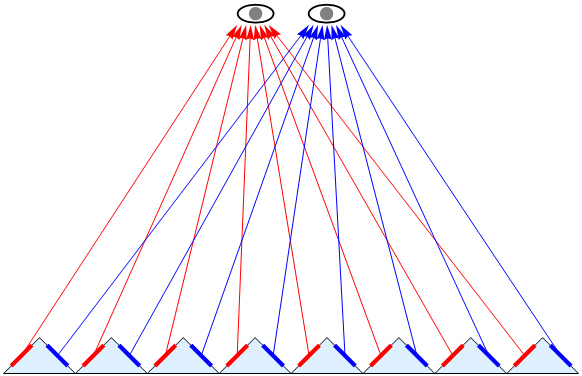
Obr. 4. Princip funkce 3D displeje.
Na stejném principu jsou vyrobeny i některé pohlednice nebo obrázky pro děti.
Kromě tohoto principu existují i další možnosti vzniku 3D obrazu, které se používají u televizorů (viz např. [3]).
Testování
Testování je většinou ta méně záživná část učitelské práce, protože je časově poměrně náročná: vymyslet testy takové, aby všechny skupiny byly navzájem porovnatelné obtížností, obětovat část hodiny na napsání testu a následnou opravu a potom všechny testy spravedlivě ohodnotit. Během všech uvedených fází testování může učitel udělat chybu, kterou pak někteří žáci mohou vnímat jako zákeřnost či nefér jednání.
PEXESO
Žáky lze ale testovat také jinak. Pro učitele to bude sice opět práce navíc, ale žáky (na základě vlastní zkušenosti) tento způsob testování baví a z hlediska naplňování RVP je naprosto ideální: žáci kooperují, vyjadřují vlastní názory, argumentují ve prospěch své teorie, … Žáci sice pracují ve skupinách, a proto by se mohlo zdát, že slabší spoléhají na ty dobré a pouze přihlížejí. Z několika testování tohoto druhu, které jsem provedl, ale vím, že tomu tak není vždy. Často i slabší žáci přispějí s dobrou myšlenkou a hlavně si všichni ujasní danou problematiku.
Inspirací k tomuto způsobu testování byla diplomová práce [4], kterou představila RNDr. Irena Dvořáková na svém workshopu na semináři Jak učím fyziku? ve Vlachovicích v roce 2011. Použil jsem námět, který autorka nazvala GRAFSESO. Pravidla a vyhodnocení jsem už ale přizpůsobil svému stylu výuky.
Postupně jsem si připravil několik sad kartiček, kterým jsem začal říkat standardně PEXESO, do výuky fyziky a (zatím hlavně) matematiky.
V současné době mám připraveny vlastní kartičky do fyziky na téma opakování za přibližně 2,5 roku výuky a do matematiky na témata výroky, množiny, lineární funkce včetně funkcí s absolutní hodnotou a kvadratické funkce včetně funkcí s absolutní hodnotou. Opakování (resp. testování) probíhá vždy stejným způsobem: žáci vytvoří 8 skupin (mám 8 shodných sad) a dostanou dvě sady kartiček, které jsou navzájem promíchané. Na jednom typu kartiček jsou např. grafy funkcí nebo výroky a na druhém typu kartiček pak předpisy daných funkcí nebo symbolické vyjádření výroku. Žáci mají za úkol přiřadit odpovídající si kartičky k sobě. Tato aktivita trvá přibližně 15 minut a během ní spolu žáci ve skupince spolupracují a snaží se najít správné řešení. Některé kartičky jsou záměrně podobné (viz obr. 5), aby žáci museli o úloze skutečně přemýšlet. Podle rychlosti přiřazení kartiček k sobě pak žáci získají odstupňované odměny: ti nejrychlejší jedničku a postupně snižující se počet plusů, na základě kterých (a to už žáci vědí) mohou později získat pěknou známku.
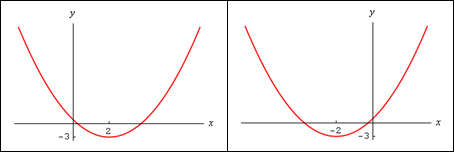
Obr. 5. Ukázka grafů na téma kvadratické funkce.
V případě zájmu o tato PEXESA je možné kontaktovat autora a materiál bude zaslán v elektronické podobě.
Závěrečný test pro 3. ročník technického lycea
V rámci závěrečného opakování učiva nejen třetího ročníku jsem připravil pro žáky technického lycea test, který byl velmi atypický. Obsahoval totiž kromě standardních úloh i úlohy, které vycházely z praktického použití fyzikálních poznatků. Nutno předeslat, že se všemi úlohami se žáci setkali v rámci cvičení z fyziky, kdy ve skupinkách zkoumali čočky, zrcadla, parametry fotoaparátu, …
Připravil jsem čtyři varianty testu. Test byl vytištěn oboustranně na papíru formátu A4 a spolu s dalšími pomůckami byl vložen do průhledných plastových sáčků (tzv. euroobaly). Každý žák tedy dostal svůj sáček s testem a pomůckami.
Následuje ukázka jedné varianty testu:
1. Dvě malé vodivé kuličky (každá o hmotnosti m) jsou zavěšeny na nevodivých vláknech, jejichž hmotnost je zanedbatelná vzhledem ke hmotnosti kuliček. Vlákna visí svisle a kuličky se navzájem dotýkají. Popište, co se stane, jestliže každou z kuliček nabijeme stejným záporným nábojem. V situaci po nabití kuliček zakreslete všechny síly, které na kuličky působí, a napište jejich názvy.
2. Vysvětlete, jak se liší akord od složeného tónu.
3. Kojenec je v dané vzdálenosti slyšet s hlasitostí 70 dB. Kolik kojenců najednou slyšíme ve stejné vzdálenosti, je-li jejich celková hlasitost přibližně 77 dB?
4. Určete název přiložené součástky (v sáčku byl rezistor nebo kondenzátor). Jakou fyzikální veličinou je tato součástka charakterizována? Jaká je hodnota této veličiny u dané součástky? Jaký význam má tato součástka v elektrickém obvodu? Jaký elektrický proud jí bude procházet, připojíme-li ji a) ke zdroji stejnosměrného napětí 15 V, b) ke zdroji střídavého napětí 60 V s frekvencí 50 Hz?
5. Určete následující parametry žárovky, která se nacházela v přiloženém obalu (v sáčku byla krabička od žárovky nebo úsporné zářivky): výkon, jmenovité napětí, jmenovitý proud, odpor vlákna žárovky, světelný tok, svítivost (za předpokladu bodového zdroje světla), osvětlení knihy ve vzdálenosti 2 m od zdroje světla, na kterou dopadá světlo kolmo, a spotřebu za dobu předpokládané životnosti žárovky.
6. Vysvětlete princip činnosti polarizačních filtrů, které používají fotografové při fotografování. Při pořizování jakých záběrů tyto filtry nasazují na objektiv fotoaparátu?
7. Určete typ přiloženého zrcadla (v sáčku bylo duté nebo vypuklé zrcadlo). Zdůvodněte. V případě, že to je možné, určete jeho ohniskovou vzdálenost. Popište a zdůvodněte svůj postup. Nakreslete schéma tohoto experimentu.
8. Jakým směrem se primárně pohybují čočky objektivu fotografického přístroje při přeostření z fotografování detailu lidské tváře na fotografování velmi vzdálených předmětů? Zdůvodněte. Proč je v textu první části otázky použito slovo „primárně“? Vysvětlete.
9. Jak se liší fotografie zobrazené na přiložených obrázcích? (V sáčku byly fotografie lišící se hloubkou ostrosti nebo zaostřením na popředí resp. pozadí snímku.) Napište správný název vlastnosti, která obě fotografie odlišuje, a vysvětlete, jaké parametry a jak musel fotograf při pořizování těchto snímků nastavit.
10. Napište názvy tří fyzikálních veličin, které mají stejnou hodnotu (resp. velikost) v Praze i na dně Mariánského příkopu. Napište názvy tří fyzikálních veličin, jejichž hodnoty (resp. velikosti) se v obou uvažovaných místech liší. V tomto případě také napište, jak se daná fyzikální veličina změní při přesunu uvažovaného experimentálního zařízení, které popisuje, z Prahy na dno Mariánského příkopu.
Literatura
[1] http://fyzika.jreichl.com/main.article/view/508
[2] http://fyzika.jreichl.com/main.article/view/1534
[3] http://fyzika.jreichl.com/main.article/view/1535
[4] Šrajlová M.: Katalog námětů k opakování učiva fyziky na ZŠ formou hry, diplomová práce MFF UK Praha, Praha 2005