O příspěvku
PDF ke staženíVěda a hra – to je Kroužek fyziky na MFF UK
Abstrakt
Kroužek fyziky na Matematicko-fyzikální fakultě Univerzity Karlovy (MFF UK) v Praze je již léta otevřen zejména středoškolákům, které zajímá fyzika a kteří se jí chtějí věnovat ve svém volném čase. V následujícím článku, který je určen zejména učitelům fyziky na základních a středních školách, uvádíme dva náměty do jejich výuky, příp. do fyzikálních seminářů a kroužků. Součástí článku jsou také odkazy na další inspirativní témata, fotografie a videa, která mohou učitelé využít ve své výuce.
1 Stručně o Kroužku fyziky na MFF UK
Kroužek fyziky pořádaný Katedrou didaktiky fyziky (KDF) na Matematicko-fyzikální fakultě Univerzity Karlovy v Praze má mnohaletou tradici sahající až do 70. let 20. století. V posledních deseti letech byli jeho vedoucími Mgr. Miroslav Jílek (v letech 2001 až 2004, viz [1]) a RNDr. Vojtěch Žák, Ph.D. (od roku 2004). Od roku 2007 se na přípravě kroužku významně podílí také Bc. Martin Konečný.
Na kroužek fyziky mohou bezplatně chodit studenti středních škol a další zájemci (často to jsou jejich kamarádi, někdy dokonce rodiče), které zajímá fyzika. Na kroužku se zabýváme nejrůznějšími tématy – od teorií moderní fyziky (např. speciální teorie relativity) až po sestrojování jednoduchých mechanických zařízení – jako je např. mechanická housenka, lodička na reaktivní pohon atd. Účastníci mohou přijít s vlastním tématem, do kterého se pak můžeme společně ponořit. Experimentujeme, vyrábíme, chodíme na exkurze a vědecká pracoviště, zveme si vědce na přednášky, počítáme, přemýšlíme, divíme se... zkrátka děláme to, co nás baví – fyziku!
Kroužky probíhají od října do června, tradičně každý čtvrtek. Aktuální informace o organizaci kroužku v daném roce je možné nalézt na webové stránce [2].
2 Námět na laboratorní práce z mechaniky
V této kapitole uvedeme podrobně popsaný námět na laboratorní práce, který byl na kroužku fyziky realizován. Jedná se o systém vhodných aktivit, při kterých žáci provádějí jak experiment, tak se nad zkoumanými jevy teoreticky zamýšlí.
Otázka a úkol: Jak daleko dostříkne voda otvorem v boku PET láhve naplněné vodou? Na čem tato vzdálenost závisí? Řešte:
a) na základě analýzy fyzikálních jednotek,
b) na základě experimentu,
c) teoreticky.
Příprava
Pomůcky: PET láhev o objemu 2 l, lihový fix, pravítko o délce 30 cm, větší miska, špendlík, obyčejná tužka, čajová svíčka, sirky, voda, (písek do akvária)
Provedení: Do dvoulitrové PET láhve uděláme v určité výšce h1 nad dnem otvor. Ten můžeme vytvořit tak, že běžný špendlík zabodneme do obyčejné tužky, jeho hlavičku zahřejeme nad plamenem svíčky (např. čajové) a potom hlavičkou protavíme otvor do boku lahve. Otvor bude mít průměr přibližně 2 mm. Od otvoru směrem k hrdlu lahve můžeme ještě fixem udělat stupnici, např. po 1 cm. Láhev naplníme vodou, hrdlo necháme otevřené, umístíme ji do větší misky a pozorujeme vytékání vody.
Pozorování: Je patrné, že s klesající vzdáleností h2 volné hladiny od vytvořeného otvoru (vlastně hloubka otvoru pod hladinou), klesá vzdálenost d, do které voda dostříkne.
Řešení A – na základě analýzy fyzikálních jednotek
Na kterých veličinách může vzdálenost d, kam dostříkne voda a kterou měříme vodorovně od „paty“ láhve, záviset? Žáky často napadne hloubka otvoru pod hladinou, tíhové zrychlení („gravitace“), výška otvoru nad dnem nádoby, atmosférický tlak, teplota vody, …
Některé veličiny můžeme na základě analýzy jejich fyzikálních jednotek vyloučit. Např. tíhové zrychlení má jednotku m·s-2, ale vzdálenost d musí vyjít v metrech. Potřebovali bychom tedy ještě další veličinu, která by obsahovala jednotku sekunda a která by se pak vhodně zkrátila. Žádná taková nás ale nenapadá. Obdobně můžeme vyloučit další veličiny s výjimkou dvou, které měříme v metrech: hloubka otvoru pod volnou hladinou vody h2 a výška otvoru nad dnem nádoby h1.
S veličinami h1 a h2 můžeme provést např. tyto matematické operace: \( h_1+h_2,\ h_1-h_2,\ \Large{\frac{h_1}{h_2}}\normalsize,\ h_1 h_2\). Otázkou je, která z těchto operací může dát požadovanou vzdálenost d. První možnost h1+h2 vypadá na první pohled logicky, ale např. pro h2 = 0 , tj. situaci, kdy je volná hladina u otvoru, musí vyjít d = 0 (vzdálenost se zmenšila až na 0 cm a voda přestane vůbec stříkat), zbývá h1, což tedy nemůže být požadovaná vzdálenost d. Druhou možnost h1−h2 může obdobně vyloučit, protože pro h1 = 0 bychom dostali vzdálenost −h2, což je „nefyzikální“. Třetí možnost \( \Large{\frac{h_1}{h_2}} \) také nevyhovuje, protože je bezrozměrná (nemá jednotku metr). Poslední možnost h1h2 řeší nedostatek první možnosti, ale vychází v jednotce m2. Použijeme tedy odmocninu a můžeme předpokládat, že \(d=k\sqrt{h_1 h_2}\), kde k je číselná konstanta.
Řešení B – na základě experimentu
Pomůcky a provedení jsme uvedli výše. Pravítko umístíme do větší misky a vodu můžeme nechat stříkat přímo na něj. Tabulku s naměřenými hodnotami h2 a d (na kroužku fyziky pro h1=12 cm) a dopočítanou konstantou kexp uvádíme níže:
| \( \frac{h_2}{\mathrm{cm}} \) |
\( \frac{d}{\mathrm{cm}} \) |
\(k_\mathrm{exp} = \frac{d}{\sqrt{h_1 h_2}}\) |
| 12 |
21,5 |
1,8 |
| 11 |
20,0 |
1,7 |
| 10 |
19,5 |
1,8 |
| 9 |
18,0 |
1,7 |
| 8 |
16,5 |
1,7 |
| 7 |
15,5 |
1,7 |
| 6 |
13,5 |
1,6 |
Z tabulky je vidět, že experiment podporuje řešení A s tím, že konstanta kexp ≈ 1,7
Řešení C – teoretické
Z teoretického hlediska se jedná o vodorovný vrh (pohyb složený z rovnoměrného pohybu ve vodorovném směru a volného pádu) s počáteční rychlostí (rychlost výtoku vody z láhve) o velikosti v0. Pro vzdálenost, kam voda dostříkne, bude tedy platit d = v0t, kde t je doba, za kterou voda dopadne na podložku (doba trvání vodorovného vrhu). Ve vodorovném směru se totiž jedná o rovnoměrný pohyb. Ve svislém směru jde o volný pád, tudíž \(h_1 = \frac{1}{2}gt^2\), kde g je velikost tíhového zrychlení. Odtud dostáváme \(t=\sqrt{\frac{2h_1}{g}} \). Dále můžeme použít Bernoulliho rovnici. Porovnáme-li situaci těsně před otvorem ve vodě a těsně za otvorem (ve vzduchu, resp. vakuu), dostaneme \( \frac{1}{2}\rho v_0^2 = h_2 \rho g \), odkud \( v_0 = \sqrt{2h_2 g}\).
Nyní můžeme postupně dosadit do vztahu pro d a obdržíme \(d = v_0 t = \sqrt{2h_2 g}\sqrt{\frac{2h_1}{g}} = 2\sqrt{h_1 h_2} \). Je zřejmé, že teoretické řešení je v souladu s řešením A a nepopírá zcela ani výsledek řešení B.
Diskuze
Experimentální řešení B se od teoretického (kexp < 2) liší zejména díky tomu, že v teoretickém řešení neuvažujeme odpor vzduchu a považujeme vodu za ideální kapalinu. Neuvažujeme ani tření mezi vodou a okrajem otvoru, kterým protéká.
Ještě více vzdálen modelu ideální kapaliny je svými vlastnostmi jemný písek do akvárií, který sice „teče“, ale v obdobném experimentu bude dopadat do prakticky stále stejné vzdálenosti. (Doporučujeme udělat pro pokus s pískem do láhve větší otvor o průměru asi 3 mm).
Pozornější experimentátoři si všimnou, že hladina vody v láhvi neklesne až k otvoru, ale zastaví se několik mm nad jeho úrovní. Tento fakt můžeme předložit žákům jako problémovou úlohu. (Je to dáno pružností povrchové vrstvy kapaliny a z rovnosti velikostí hydrostatické tlakové síly a povrchové síly můžeme určit povrchové napětí. Vychází řádově správně.)
3 Námět[1] na jednoduchý experiment z optiky
Pomůcky: skleněná zkumavka nebo odměrný válec (nejlépe bez stupnice), glycerol, skleněná tyčinky (na míchání z chemické laboratoře)
Provedení: Zkumavku naplníme do ¾ glycerolem a ponoříme do něho skleněnou tyčinku. Pozorujeme proti bílému podkladu.
Vysvětlení: Index lomu běžného skla (n = 1,5 – 1,6) a glycerolu (n = 1,47) jsou velmi podobné. Paprsek prochází soustavou zkumavka-glycerol-skleněná tyčinky téměř bez lomu, a předmět tudíž není skoro vidět. Je třeba dodat, že při „nevhodném“ natočení jsou okraje tyčinky více viditelné, jelikož těsně na rozhranní dochází k lomům paprsků (na povrchu tyčinky mohou být nečistoty, vzduchové bublinky apod.).
Náměty: Považujeme za důležité se studentů zeptat, proč není skleněná tyčinky téměř vidět. Většinou chybně odpovídají, že je to díky hustotě glycerolu, ... Dalším úkolem může být hledání předmětů, které by měly index lomu ještě blíže indexu lomu glycerolu (například některé plasty). Uvedený úkol můžeme spojit s laboratorní úlohou, kdy studenti měří vhodnou metodou index lomu uvedených látek.
Na následujících pár řádcích bychom rádi zmínili některé vlastnosti a použití glycerolu. Rádi bychom po četných dotazech z řad učitelů uvedli, jak spolu souvisí glycerol a glycerín (jedná se o stejnou látku) a zmínili bychom se o nebezpečnosti této chemické látky.
GLYCEROL
- starším názvem glycerín, triviální název glycerol, avšak systematický název propan-1, 2, 3-triol (trojsytný[2] alkohol)
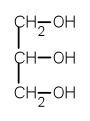
- Název glycerol vznikl z názvů jeho dvou vlastností. Je sladký (řecky glykys = sladký) a má velkou dynamickou viskozitu[3] (latinské cera = vosk).
Glycerol se běžně používá v kosmetických přípravcích, zubních pastách a v potravinách jako aditivum (E422, tzv. modifikované škroby a zahušťovadla). Je důležitou biogenní sloučeninou, jelikož ve formě esterů je součástí tuků. Jeho sloučenina nitroglycerin je složkou výbušnin (dynamit, ...).
Glycerol je slabě jedovatý (nejnižší toxická dávka je přibližně 90 g), v nízkých koncentracích je prakticky neškodný.
Běžně jej seženete v drogeriích, lékárnách, či u svých kolegů učitelů chemie, kteří jej používají jako mazadlo na gumové hadičky.
4 Další náměty využitelné ve výuce
V následujícím bychom chtěli poskytnout výběr materiálů, které lze využít při výuce fyziky. Jedná se o fotografie, videa či náměty na pokusy, které v kroužku provádíme. O fungování webu se starají studenti a není recenzován.
• Jak jednoduše spočítat rychlost světla, co udělá hroznové víno, vejce v mikrovlnné troubě apod.
• Zimní fyzika Tání ledu, vznik rampouchů, cirkulace vzduchu nejen v místnosti.
• Hologramy Výroba vlastních hologramů.
• Předvánoční show s kapalným dusíkem []
Stalo se již tradicí, že poslední kroužek před Vánoci je show s kapalným dusíkem. Můžete zhlédnout zajímavé experimenty a nahlédnout, jak se vyrábí zmrzlina.
Na stránkách Kroužku fyziky [2] je samozřejmě i další spousta zajímavých námětů. Pokud některé z nich využijete, budeme rádi.
5 Závěr
Kroužek fyziky na KDF MFF UK byl a doufáme, že i nadále bude. Letošní rok 2010/2011 bychom chtěli pojmout trochu netradičně, a to zejména prací na dlouhodobějších projektech. Studenti tak více proniknou do daného tématu, naučí se ověřovat své hypotézy, prezentovat výsledky své práce, což je i v reálném životě velmi důležité. Tyto práce budou střídány s kroužky, kde si budeme hrát a pozorovat tak, jak tomu bylo doposud. Veškeré materiály, které vzniknou (listy pro laboratorní práce, fotografie, videa, ...), budeme uveřejňovat na webových stránkách Kroužku fyziky [2] a jsou vám plně k dispozici. Pokud je nějakým způsobem využijete, budeme rádi za zpětnou vazbu. Těšíme se na vaše studenty v Kroužku fyziky!
Literatura
[1] http://fyzweb.cuni.cz/dilna/krouzky/uvod/uvodni.htm
[2] http://www.krouzek-fyziky.ic.cz/
[3] Mikulčák, J.; Charvát, J.; Macháček, M.; Zemánek, F.: Matematické, fyzikální a chemické tabulky a vzorce pro střední školy. Praha: Prometheus, 2003. ISBN 978-80-7196-264-9.
[1] Námět byl získán od Mgr. Zdeňka Poláka, Gymnázium Náchod.
[2] obsahuje 3 skupiny -OH
[3] Dynamická viskozita glycerolu je asi 1000krát větší než viskozita vody (při 20 °C). [3]