Základy elektrostatiky v pokusech (Coulombův zákon, kondenzátor)
Stejně jako učebnice, tak pravděpodobně i většina vyučujících začíná kapitolu o elektřině a magnetismu elektrostatikou. Tento článek se zabývá dvěma ze základních pojmů tohoto tématu, kondenzátorem a Coulombovým zákonem, a dává námět na několik experimentů, které by mohly pomoci studentům lépe pochopit a „osahat“ si fyzikální jevy, které s nimi souvisí.
Tento článek lze rovněž chápat jako učitelské poznámky popisující možnosti zavedení kondenzátoru do výuky, a ověření Coulombova zákona.
Náměty na popsané pokusy byly nalezeny v [1], [2] a [4].
Jednoduchý kondenzátor
Kondenzátorem rozumíme „součástku“, kterou lze použít pro uchování elektrického náboje a lze ji použít jako dočasný zdroj napětí. Kondenzátory mohou mít různý tvar a různou konstrukci. Pod pojmem kondenzátor si však velice pravděpodobně představíme jeho základní variantu, která dala vzniknout i jeho schematické značce – dvě vzájemně rovnoběžné vodivé desky, mezi nimiž je buď vzduch, nebo jiné dielektrikum.
Pro kapacitu tohoto kondenzátoru existuje velmi jednoduchý vztah (1), který sice není těžké úvahou odvodit, na druhou stranu jej není těžké ani ověřit – a to už se pravděpodobně v mnoha případech neděje. Nemá-li učitel k dispozici jistě velmi pěknou pomůcku, dvě kovové desky, které by bylo možné vzdalovat od sebe a měnit jejich účinnou plochu, může je nahradit obyčejným alobalem a kapacitu pak měřit „lepším“ multimetrem, tj. takovým, který umí měřit kapacitu.
\[\tag{1} C= \epsilon\frac{S}{d} \]Celá myšlenka je velmi jednoduchá. Desky kondenzátoru vyrobíme např. z hliníkové fólie a uložíme mezi listy knihy. Je tedy dobré zvolit takovou velikost alobalu, která odpovídá velikosti stránek knihy. K jednotlivým fóliím připojíme svorky multimetru.
Pro určení závislosti kapacity C na vzdálenosti desek d budeme měnit počet listů mezi deskami. Do grafu pak vyneseme závislost \( C(d) \) a \( C(1/d) \), přičemž vzdálenost může být uvedena jak v počtech listů mezi deskami, tak v milimetrech. První varianta je zřejmě jednodušší a rychlejší a dle mého soudu je i výhodnější pro soustředění se na závislost kapacita vs. vzdálenost – studenti nejsou rušení přepočítáváním počtu stránek na milimetry. Studenti zjistí, který z grafů „vypadá“ lineárně a zda je tak kapacita C přímo úměrná d, či 1/d (viz grafy 1 a 2).
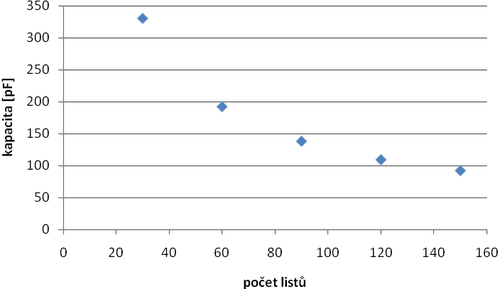
graf 1: Experimentálně určená závislosti kapacity na počtu listů mezi deskami
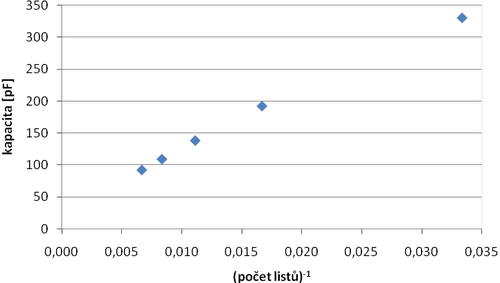
graf 2: Experimentálně určená závislosti kapacity na převrácené hodnotě počtu listů mezi deskami
Pro získání závislosti kapacity C na účinné ploše desek S postačí, budeme-li zmenšovat desky vždy na polovinu[1] a při každém zmenšení určíme kapacitu kondenzátoru. Velikost plochy udáváme v násobcích (dílech) velikosti stránky knížky (resp. původní desky). Z didaktických důvodů necháme studenty rovněž vytvořit grafy obou závislostí \( C(S) \) a \( C(1/S) \) [2]. Studenti tedy zjistí, zda je kapacita C přímo úměrná S, či 1/S.
Kombinací těchto odvozených závislostí není problém určit úměrnost obsahující závislost na d i S.

obrázek 1: Měření kapacity vytvořeného kondenzátoru: a) diagram, b) reálné zapojení
Pomůcky
• alobal (hliníková fólie)
• kniha s větším množstvím stránek (čím větší formát, tím lepší)
• multimetr s možností měření kapacity
• případně vodiče s krokodýlky, posuvné měřítko a metr
Příklad pracovního listu
Část I – Kapacita v závislosti na vzdálenosti desek (fólií)
1) Opatřete si silnou knihu a dva kusy alobalové fólie velikosti stránky této knihy
2) Umístěte fólie do knihy tak, aby mezi nimi bylo 30 listů, tj. například jednu na stranu 200, druhou na stranu 260.
3) Připojte červenou sondu k jedné fólii, černou k druhé fólii a knihu zavřete.
4) Otočte voličem multimetru na symbol –||– (měření kapacity).
5) Kapacita, kterou budete měřit bude v nanoFaradech. (Na displeji byste měli vidět „nF”.) Výslednou kapacitu zaneste do tabulky.
6) Opakujte měření pro různé množství listů mezi fóliemi.
7) Naměřená data vložte do Excelu a vytvořte 2 grafy:
a) graf závislosti kapacity na počtu listů,
b) graf závislosti kapacity na (počtu listů)-1.
| Počet listů |
(Počet listů)-1 |
Kapacita (nF) |
| 30 |
1/30 |
|
| 60 |
1/60 |
|
| 90 |
1/90 |
|
| 120 |
1/120 |
|
| 150 |
1/150 |
|
Který z grafů vypadá lineárně?
a) Kapacita vs Počet listů
b) Kapacita vs (Počet listů)-1
Lineární závislost ukazuje, že veličiny jsou si přímo úměrné. Která z následujících úměrností je tedy správná? (C představuje kapacitu kondenzátoru a d vzdálenost elektrod (fólií). Vzdálenost odpovídá počtu listů mezi fóliemi.)
\[ C \sim \frac{1}{d} \qquad C \sim d \]Část II – závislost kapacity na velikosti desek (fólií)
1) Změřte a zapište kapacitu vašeho kondenzátoru při oddělení jeho desek např. 50 listy.
2) Opakujte měření pro různé velikosti fólií. Postupně je zmenšujte – přehýbejte vždy napůl. Naměřené kapacity zapište do následující tabulky.
3) Na základě vašich naměřených dat zpracujte v Excelu dva grafy:
a) graf závislosti kapacity na velikosti plochy desek,
b) graf závislosti kapacity na (velikost plochy desek)-1.
| Plocha |
(Plocha)-1 |
Kapacita (nF) |
| S |
1 / S |
|
| 0.5 * S |
2 / S |
|
| 0.25 * S |
4 / S |
|
| 0.125 * S |
8 / S |
|
| 0.0625 * S |
16 / S |
|
Který z grafů vypadá lineárně?
a) Kapacita vs Plocha
b)Kapacita vs Plocha-1
Lineární závislost říká, že veličiny si jsou přímo úměrné. Která z následujících úměrností je tedy správná? (C je kapacita kondenzátoru, S je plocha desek.)
\[ C \sim \frac{1}{S} \qquad C \sim S \]Část III – Rovnice kapacity deskového kondenzátoru
Kombinací obou zjištěných úměrností formulujte jednu, která bude obsahovat oba fakty (závislost kapacity na d i na S)
C ∼
Abychom přetvořili vztah úměrnosti na skutečnou rovnici (kde budou už správně „sedět“ jednotky), musíme přidat konstantu úměrnosti. V tomto případě se jedná o \( \varepsilon \), která se nazývá permitivita prostředí. Nejnižší permitivitu má vakuum (\(\varepsilon_0 = 8,85\cdot 10^{-12}\,\mathrm{C^2/Nm^2}\)). Permitivita každého jiného prostředí je větší a je udávána v násobcích permitivity vakua jako \(\varepsilon=\varepsilon_r \cdot \varepsilon_0\), kde \(\varepsilon_r\) je právě onen násobek a nazývá se relativní permitivita prostředí.
Doplňte správný tvar rovnice pro kapacitu deskového kondenzátoru.
\[C=\varepsilon \frac{\ }{\ } = \varepsilon_r \varepsilon_0 \frac{\ }{\ } \]Další možné využití experimentální sestavy
Pokud bychom určovali vzdálenost desek (použitých hliníkových fólií) a jejich velikost v „tradičních“ jednotkách (metrech), budeme mít dostatek údajů k tomu, abychom určili permitivitu prostředí mezi deskami. V našem případě se jedná o papír, jehož permitivita je udávána přibližně jako \( \varepsilon_r = 3,5\) (viz např. [2]).
Navíc, když už jsme fólie (desky kondenzátoru) zmenšili, můžeme předvést[3], že písmenko S ve výsledném vztahu není plocha jednotlivých desek, ale jejich „účinná“ plocha, tj. plocha, kterou se překrývají[4].
Ověření Coulombova zákona
Coulombův zákon (2) představuje jeden ze základních poznatků elektrostatiky, který je představován studentům na střední škole. Jakým způsobem však jednoduše ověřit, případně odvodit, platnost tohoto zákona?
\[\tag{2}F_e = \frac{1}{4\pi\varepsilon}\cdot\frac{Q_1 Q_2}{r^2} \]Coulombův zákon. Dva bodové náboje na sebe vzájemně působí elektrickou silou. Tato síla je přímo úměrná velikosti jednotlivých nábojů a nepřímo úměrná druhé mocnině jejich vzdálenosti. Jsou-li tyto náboje souhlasné, síla je odpudivá; jsou-li opačné, síla je přitažlivá.
Nebudeme zde popisovat ověření celého zákona, ale zaměříme se pouze na ověření závislostí velikosti síly Fe na převrácené hodnotě druhé mocniny vzdálenosti bodových nábojů 1/r2 a na velikosti nábojů Q1 a Q2.
Aparatura, kterou budeme používat, sestává z vysokonapěťového zdroje (případně indukční elektriky, van der Graafova generátoru, apod.), tří ping-pongových míčků nastříkaných vodivou barvou (můžeme použít i vánoční ozdoby – menší koule) připevněných na nevodivých stojáncích (zde je použito brček), digitální váhy s rozlišením alespoň 0,01 g, pravítko (metr), stativový materiál (viz obrázek 2a).


obrázek 2: a) Aparatura pro demonstraci Coulombova zákona b) Váhy použité pro „měření“ elektrické síly
Princip celého měření a určování velikosti elektrické síly je poměrně jednoduchý. Jako „siloměr“ budeme využívat již zmíněné elektronické váhy. Ideální je, pokud mají váhy možnost tárování[5].
Postup pro změření velikosti síly v dané vzdálenosti kuliček r:
• Na váhy postavíme jednu z kuliček na stojánku, nad ni (do větší vzdálenosti) do stativu umístíme druhou.
• Vytárujeme váhy.
• Obě kuličky nabijeme (např. pomocí VN zdroje) V našem případě (viz obr 2) jsme se dotkli každé z kuliček připojené ke stejné svorce zdroje. Obě kuličky pak měly stejný náboj.
• Přiblížíme jednu z kuliček.
• Na displeji odečteme „přidanou hmotnost“ kuličky \(\Delta m\). Elektrická síla \(F'_e \) působící mezi kuličkami je pak přímo úměrná \(\Delta m\) a to podle vztahu \(F'_e=\Delta m \cdot g\).
Jelikož nemáme k dispozici bodové náboje, dochází na kuličkách díky vzájemnému ovlivňování nábojů k jejich přeuspořádání. Tím se mění i velikost síly působící mezi dvěma kuličkami ve vzájemné vzdálenosti r jejich středů. Coulombův zákon v našem reálném případě by pak měl tvar[6]
\[\tag{3} F'_e = \frac{Q_1 Q_2}{4\pi \varepsilon r^2}\cdot \left[1- 4\left(\frac{a}{r}\right)^3 + 14\left(\frac{a}{r}\right)^6 - \ldots \right]\] kde a je poloměr kuliček. Člen korekce \(14\left(\frac{a}{r}\right)^6\) je však stejně jako všechny následující tak malý, že jej můžeme společně s ostatními zanedbat a rovnice bude mít tvar \[\tag{3} F'_e = \frac{Q_1 Q_2}{4\pi \varepsilon r^2}\cdot \left[1- 4\left(\frac{a}{r}\right)^3 \right]\]
Ověření závislosti Fe (1/r2)
Chceme-li ověřit závislost elektrické síly na druhé mocnině vzdálenosti r, nebudeme do grafu na y-ovou osu vynášet přímo sílu \(F'_e=\Delta m \cdot g\), kterou bychom „změřili“ na vahách, ale sílu \[F_e = \frac{F'_e}{\left[1- 4\left(\frac{a}{r}\right)^3 \right]} = \frac{\Delta m \cdot g}{\left[1- 4\left(\frac{a}{r}\right)^3 \right]} \] která by odpovídala vzájemnému působení dvou bodových nábojů o stejné velikosti, jako mají v experimentu použité kuličky. Na x-ovou osu vyneseme příslušné vzdálenosti r. Tato napohled podivná úprava je nutná hlavně z toho důvodu, že Excel (pravděpodobně stejně jako i jiný dostupný tabulkový procesor) je schopen fitovat pouze předdefinovanými funkcemi, mezi které patří i mocninná závislost, ale nikoli závislost, která se vyskytuje ve vztahu (4). Dostali jsme se tedy zpět k tomu, že budeme ověřovat vztah (2). Tentokrát však s tím rozdílem, že v tomto případě síla Fe není síla, kterou jsme naměřili v experimentu, ale síla s korekcí – tj. taková, kterou bychom naměřili, kdyby nedocházelo k přerozdělení náboje na kuličkách.
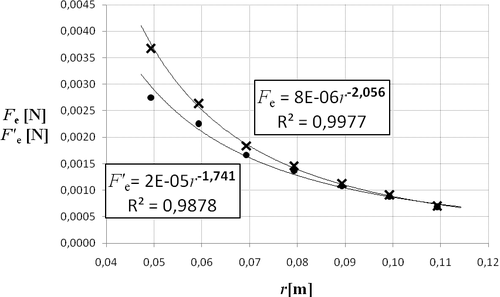
Graf 3: Porovnání závislostí skutečně naměřené síly \(F'_e\) (značka •) a síly s korekcí \(F'_e\) (značka ×).
Jak je patrné z grafu 3, tak rovnice křivky proložené daty s korekcí dobře odpovídá předpokládané závislosti (2), resp. Coulombovu zákonu. Rovněž si můžeme povšimnout, že korekce je tím větší, čím jsou si kuličky blíže.
Demonstrace závislosti Fe (Q1,Q2)
Nastavíme dvě nabité kuličky s náboji do libovolné pevné vzdálenosti (jedna z kuliček opět na vahách – stejně jako v předchozím případě) a odečteme hodnotu na vahách. Následně snížíme jeden z nábojů na polovinu tím, že se jedné z kuliček dotkneme třetí nenabitou kuličkou[7]. Váhy budou ukazovat přibližně polovinu.
Závěr
U každého z prezentovaných pokusů vás určitě napadnou další varianty. U prvního příspěvku by bylo jistě možné přidat aktivitu týkající se porovnávání permitivit různých materiálů (sklo, dřevo, plast, apod.). U druhého z pokusů například můžeme pomocí elektrostatické indukce nabít jednu z kuliček opačným nábojem a pozorovat jejich přitahování – váhy budou ukazovat zápornou hodnotu.
Vznik tohoto příspěvku byl podpořen grantem FRVŠ 1237/2010: Demonstrační experimenty pro přednášky "Fyzika I" a "Klasická elektrodynamika".
Literatura
[1] Capacitor lab - using a capacitor in a circuit. online. [cit 2010-09-02] http://webapps.lsa.umich.edu/physics/demolab/controls/FileExp.aspx?fileid=36
[2] Experiment: Parallel Plate Capacitors. online. [cit 2010-09-02] http://spot.pcc.edu/~azable/ph213/labs/213Lab4-Parallel_Plate_Capacitors.doc
[3] Permitivita. online. http://cs.wikipedia.org/wiki/Permitivita. [cit. 2010-09-01]
[4] Cortel A., Demonstrations of Coulomb’s Law with an Electronic Balance, Physics Teacher, v37 n7 p447-48, Oct 1999
[5] Larson C.O., Goss E.W., A Coulomb's Law Balance Suitable for Physics Majors and Nonscience Students, American Journal of Physics, v38, n11, pp1349-1352, Nov `70
[1] Pokud bychom chtěli proměřit závislost přesněji, bude zapotřebí větší počet hodnot a určitě si nevystačíme pouze s půlením fólie.
[2] Jistě si dovedete příslušné grafy představit. Z důvodu úspory místa je již neuvádíme.
[3] Někteří studenti na to určitě přijdou při experimentování sami.
[4] Díky tomu by mohly nastat problémy při samostatné práci studentů. Tomuto problému bychom se mohli vyhnout, kdybychom zmenšovali jen jednu z fólií. Na druhou stranu je dobré, když vznikají problémové situace a žáci (studenti) se je snaží řešit.
[5] Tj. možnost zvolit nulu.
[6] Odvozením této korekce Coulombova zákona se zabývá článek [5]. Nutnost korekce je patrná například z grafu 3.
[7] Aby se náboje rozdělily opravdu na polovinu, nesmíme se kuličkami dotýkat v blízkosti třetí kuličky. Přerozdělení náboje by bylo ovlivněno jejím elektrickým polem. Druhou možností je dotknout se kuličky (např. ve stativu) tak, aby obě kuličky (ve stativu i ta, kterou se dotýkáme) byly ve stejné vzdálenosti od kuličky stojící na vahách.