Malinová H.: Hydrostatické váhy (Veletrh 14, Brno 2009) / Sborník Veletrhu nápadů učitelů fyziky

O příspěvku

Klíčová slova

Použití

SŠ/VŠ

Pomůcky

S opravdu jednoduchými pomůckami
S jednoduchými pomůckami
S běžným vybavením kabinetu

PDF ke stažení

Hydrostatické váhy

Malinová H.

V příspěvku bude prezentována metoda hydrostatického vážení, která se používá na určování hustoty různých materiálů. Žáci si budou moci tuto metodu vyzkoušet v jednodušší verzi v podobě laboratorní úlohy.

Princip hydrostatického vážení

Metoda se používá k přesnému určení hustoty pevné látky i nepravidelného tvaru nebo kapaliny. K vážení se používá rovnoramenných vah, které jsou mírně upraveny tak, aby se předmět mohl ponořit do kapaliny známé hustoty a mohl se tedy vážit ve vzduchu nebo v kapalině (viz obr. 1., [1]).

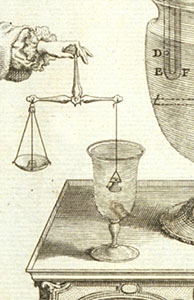
Obr. 1. Hydrostatické váhy

Kapalina těleso nadlehčuje silou rovnající se tíze kapaliny stejného objemu, jaký má ponořená část tělesa. Princip hydrostatického vážení vychází z Archimédova zákona.

Následovat budou dvě odvození: odvození vztahu (1) (viz dále) není tolik známé, odvození přesnějšího vztahu (2) je obecnější a používá se i v praxi. Odvození vztahů k určení hustoty pevných látek či kapalin lze najít např. v [2, str. 53] a [3] až [5].

Odvození vztahu (1) zahrnujícího vzdálenost

Pro jednoduchost odvození uvažujme dvě stejná tělesa (např. matky o hmotnosti m) neznámé hustoty ρ_t. Hydrostatické váhy (ozn. HV) se v tomto případě skládají z tyčky, která je opatřena stupnicí (např. nalepeným metrem, viz obr. 2. až obr. 4.).

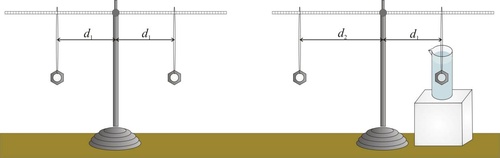
Obr. 2. HV na začátku měření (vlevo) a po nastavení rovnováhy (vpravo)

Na začátku měření, kdy jsou obě tělesa ve vzduchu, je počáteční vzdálenost d₁ pro obě ramena stejná (viz obr. 2. – vlevo). Jedno z těles následně celé ponoříme do vody o hustotě ρ_v, tím se poruší rovnováha – pro moment síly M₁ vzhledem k pevné ose otáčení umístěné uprostřed tyče platí \[ M_1 = d_1 (F_G -F_{VZ}) = d_1 mg - d_1 - \rho_V V g , \] kde \( V = \frac{m}{\rho_t}\), F_G je tíhová síla působící na závaží a F_VZ je vztlaková síla.

Aby se rovnováha obnovila, budeme pohybovat druhým závažím (neponořeným do vody) až do vzdálenosti d₂. Pro moment síly M₂ vzhledem k pevné ose otáčení umístěné uprostřed tyče platí \[ M_2 = d_2 F_G = d_2 mg .\]

Momenty sil se po nastolení rovnováhy rovnají (viz obr. 2. – vpravo) \[ M_1 = M_2 \ \Rightarrow\ d_1mg-d_1\rho_V \frac{m}{\rho_t} g = d_2 mg, \] a po úpravách dostáváme vztah \[\tag{1} \rho_t = \rho_V \frac{d_1}{d_1 - d_2}. \]

Odvození vztahů (2) a (3) zahrnujících hmotnost

Hydrostatické váhy se skládají z rovnoramenných vah upravených jako na obr. 5. a na obr. 6. (srovnej rozdíly oproti minulému odstavci). Po nastolení rovnováhy se momenty sil rovnají: jelikož se jedná o rovnoramenné váhy, stačí, aby se rovnaly síly působící na jednotlivá ramena.

Pro rovnováhu na vzduchu o hustotě ρ_VZ platí \[ F_{G_{z1}} - F_{VZ_{z1}} = F_{G_{t}} - F_{VZ_{t}} \ \Rightarrow \] \[\tag{a} m_{z1} g - \frac{m_{z1}}{\rho_{z1}}\rho_{VZ} g = m_{t} g - \frac{m_{t}}{\rho_{t}}\rho_{VZ} g\ \Rightarrow \ m_{z1}\left( 1 - \frac{\rho_vz}{\rho_z1} \right) = \ m_{t}\left( 1 - \frac{\rho_vz}{\rho_t} \right), \] kde F_G je tíhová síla, F_VZ je vztlaková síla, index z1 označuje závaží, které vyvažuje zvolené těleso ve vzduchu, a index t označuje těleso.

Pro rovnováhu po ponoření tělesa do kapaliny o hustotě ρ_k platí \[ F_{G_{z2}} - F_{VZ_{z2}} = F_{G_{t}} - F_{VZ_{t}} \ \Rightarrow \] \[\tag{b} m_{z2} g - \frac{m_{z2}}{\rho_{z2}}\rho_{VZ} g = m_{t} g - \frac{m_{t}}{\rho_{t}}\rho_{k} g\ \Rightarrow \ m_{z2}\left( 1 - \frac{\rho_vz}{\rho_z2} \right) = \ m_{t}\left( 1 - \frac{\rho_k}{\rho_t} \right), \] kde index z2 označuje závaží, které vyvažuje zvolené těleso ponořené do kapaliny.

Po vydělení rovnice (a) rovnicí (b) dostaneme následující rovnost, kterou za předpokladu, že hustoty ρ_Z1 a ρ_Z2 jsou stejné, můžeme upravit na jednodušší tvar (c).

\[\tag{c} \frac{\ m_{z1}\left( 1 - \frac{\rho_vz}{\rho_z1} \right)}{m_{z2}\left( 1 - \frac{\rho_vz}{\rho_z2} \right)} = \frac{m_{t}\left( 1 - \frac{\rho_vz}{\rho_t} \right)}{m_{t}\left( 1 - \frac{\rho_k}{\rho_t} \right)} \ \Rightarrow\ \frac{m_{z1}}{m_{z2}} = \frac{1 - \frac{\rho_vz}{\rho_t}}{1 - \frac{\rho_k}{\rho_t}}. \]

Jednoduchou úpravou dostaneme \[ m_{z1}\rho_t - m_{z1}\rho_k = m_{z2}\rho_t - m_{z2}\rho_{VZ}\] a nakonec vyjádříme \[\tag{2} \rho_t = \frac{\rho_k m_{z1} - \rho_{VZ} m_{z2}}{ m_{z1} - m_{z2}}. \]

Pokud se rozhodneme zanedbat vztlak ve vzduchu, dostaneme výraz \[\tag{3} \rho_t = \rho_k \frac{m_{z1}}{m_{z1} - m_{z2}} .\]

Různé typy hydrostatických vah aneb jak by mohlo vypadat přizpůsobení do školních lavic

Hydrostatické váhy mohou být různé, většinou však mají jedno společné: jsou příliš drahé, abychom si je mohli jako učitelé dovolit nakoupit do školních laboratoří. Nabízím zde dvě varianty hydrostatických vah, které můžeme použít při laboratorní úloze na určování hustoty pevných látek (např. str. 282, [16]). Myslím, že tuto úlohu by mohli měřit žáci, kteří už velmi dobře znají laboratorní úlohu zaměřenou na vážení a zjišťování objemu ponořením do odměrného válce nebo pomocí změření rozměrů tělesa (např. str. 276, [16]). Proto nabízím možnost, jak hydrostatické váhy vyrobit jednoduchým způsobem. Nejlepší představu poskytnou obrázky 3. až 6.

Obr. 3. Dřevěná tyčka opatřená stupnicí

Obr. 4. HV v průběhu měření

Obr. 5. HV s kovovým plíškem

Obr. 6. HV s náhradní miskou na závaží

Jako předmět, jehož hustotu budeme určovat, je docela vhodné použít matku, a to hned z několika důvodů – velmi dobře se shání, není nikterak drahá, může být z různých materiálů a dá se dobře připevnit na niť či tenké lanko.

Je potřeba přesně určit hustotu kapaliny, do které se předmět ponořuje. V praxi se nejčastěji používá pyknometru ([6]) – jedná se o malou nádobu, která má přesně definovaný objem. Lze použít také hustoměr, který je spíše k sehnání anebo určit teplotu kapaliny a dopočíst přesnou hustotu pomocí tabelovaných hodnot v tabulkách.

Výhody a nevýhody hydrostatického vážení, porovnání s přímou metodou

Pokusím se o jednoduchý nástin výhod a nevýhod hydrostatického vážení (ozn. h. vážení), jistě však lze najít i další. Přímou metodou zde rozumím použití definičního vztahu a vypočtení hustoty jako podílu hmotnosti tělesa a jeho objemu (objem pravidelných těles vypočteme na základě měření jeho rozměrů, nepravidelná tělesa ponoříme do kapaliny v odměrném válci).

• Metoda založená na h. vážení je poněkud složitější než přímá metoda, protože se zde využívá znalosti Archimédova zákona a momentu sil, tj. je potřeba zopakování učiva z různých oblastí fyziky. Možnost použití korekce na vztlak ve vzduchu dává nadanějším studentům příležitost hlouběji se seznámit s postupem, který se v praxi skutečně používá.

• Jedná se o další dva způsoby určování hustoty pevných látek, které společně s přímou metodou a dalšími metodami dávají možnost třídu rozdělit do několika pracovních skupin, které určují hustotu různým způsobem. Seznam takových aktivit se dá najít např. [7].

• U hydrostatické metody můžeme použít i jiné kapaliny, do kterých se předměty ponořují. Důležité je, aby předmět s kapalinou nereagoval. Velmi často se používá voda, která však vytváří na předmětu bublinky – na to je třeba dávat pozor.

• Metodou hydrostatickou lze určovat i hustoty kapalin ([4]). V tomto případě těleso ponoříme nejprve do kapaliny o známé hustotě (např. destilované vody) a potom do kapaliny, jejíž hustotu chceme určit.

• Metoda přímá nabízí velmi jednoduchou možnost určení hustoty pravidelných těles, které mají menší hustotu než voda, a to změřením jejich rozměrů a zvážením. Metoda hydrostatická se dá použít, pokud najdeme vhodnou kapalinu s ještě menší hustotou, než má zkoumané těleso.

• Porovnávala jsem přesnost výše uvedených metod h. vážení s referenčním měřením v laboratoři KFM MFF UK a nedospěla jsem k výrazným rozdílům ve výsledcích, pominu-li různý počet platných cifer. Metody h. vážení se ukázaly být přesnější než metoda přímá, která se nejčastěji používá při laboratorních pracích.

• Metoda se využívá v praxi (viz následující odstavec) k určování hustoty pevných látek nepravidelných tvarů. Metoda přímá se kvůli velké chybě měření nepoužívá.

Kde se tato metoda využívá

Určování hustoty se používá v různých odvětvích, například ve zdravotnictví k určení složení lidského těla ([8]), ve stavebnictví k určení pórovitosti či nasákavosti materiálů ([9]), ve vinařství k určení obsahu alkoholu ve víně ([10]), na vysokých školách jako fyzikální praktikum ([5]) a při zkoumání vlastností drahých kamenů ([11]).

Jak je tato metody stará

První zmínka o hydrostatických vahách, alespoň podle zdroje [12] a [13], sahá do druhé poloviny 9. století. Je spojena se jménem al-Rází, což byl arabský filozof a alchymista, který dokázal stanovit hustoty osmnácti kovů a drahokamů s velkou přesností. Podle [14] to byl až Galileo Galilei, kdo zdokonalil metodu vážení drahých kovů ve vzduchu a ve vodě používanou už dříve u klenotníků – sestrojil první hydrostatické váhy ([15]) a roku 1586 o nich napsal vědeckou práci.

Galileo Galilei či jiní neurčovali přímo hustotu vzorků, ale jejich relativní hustotu – tím rozumíme poměr hustoty neznámé pevné látky či kapaliny k hustotě referenční látky (nejčastěji se jedná o vodu při 20 °C za normálního tlaku).

Závěr

Výše popsané metody hydrostatického vážení je možné úspěšně využít při školních laboratorních cvičeních. Žáci si zopakují látku z různých oblastí fyziky a použití odlišných variant měření několika skupinami žáků umožní rozvinout diskuzi např. o přesnosti měření a zanedbávání různých vnějších vlivů (vztlaková síla působící na těleso ve vzduchu a podobně).