Experimentální studium náhlého zmrznutí podchlazené vody
Nina se dvakrát třikrát rozmáchla a hodila led do klidné vody….
Okamžitě zazněl silný praskot, který se nesl až k obzoru.
Galické moře na celém povrchu zamrzlo.
Jules Verne, Na kometě
Podchlazení, nebo také přechlazení kapaliny je dobře známý jev, při kterém existuje látka v kapalné fázi i za teplot nižších, než by odpovídalo teplotě fázového přechodu při daném tlaku. Podchlazená voda se běžně nachází v oblacích, kde může její teplota v kapalném stavu dosáhnout až -40ºC. Silně podchlazený je i octan sodný (resp. jeho trihydrát) v tzv. hřejivých polštářcích, které po iniciaci tuhnutí uvolňují krystalizační teplo.
Existence tohoto jevu souvisí s problematikou nukleace krystalizačních zárodků, kterou samotná fázová změna začíná a lze ji v jistém zjednodušení vysvětlit následujícími energetickými úvahami [1].
Předpokládejme, že náhodnou fluktuací vznikl malý zárodek pevné fáze uvnitř kapaliny. Vytvoření zárodku doprovází vznik pevnějších chemických vazeb, což vede ke snížení energie ΔEV systému. Právě tato energie se uvolňuje jako tzv. skupenské teplo tuhnutí. Současně však vzniká nové rozhraní kapalina – pevná látka, s jehož existencí je spojena povrchová energie ΔES (ve středoškolské fyzice se povrchová energie zmiňuje v souvislosti s povrchovým napětím kapalin). Pro celkovou změnu energie systému ΔEC můžeme psát[1] \[\tag{1} ΔE_C = ΔE_V + ΔE_S = -Ar^3 + B r^2 ,\] kde r je poloměr nebo jiný charakteristický rozměr zárodku, A a B jsou materiálové konstanty. Záporné znaménko popisuje úbytek energie (zde úměrné vzniklému objemu zárodku), kladné znaménko její nárůst (úměrné ploše rozhraní). Grafické znázornění popsaných závislostí je na obr. 1.
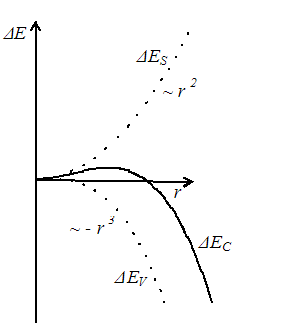
Obr. 1
Z uvedeného je zřejmé, že počáteční fáze růstu zárodku vede ke zvyšování energie systému, a proto neprobíhá spontánně, podobně jako voda sama neteče do kopce. Nicméně při velkém podchlazení může náhodnou fluktuací zárodek přerůst kritickou velikost, tím překonat energetickou bariéru a definitivně odstartovat fázovou změnu. Tento způsob se nazývá homogenní nukleace. Častější je však případ tzv. heterogenní nukleace, kdy nadkritický nukleační zárodek vzniká na nečistotě či defektu, které snižují povrchovou energii zárodku. Toto vede ke snížení kritické velikosti a usnadnění vzniku zárodku nadkritického rozměru.[2].
Jakmile jediný zárodek překoná kritickou velikost, fázová změna dále pokračuje již velmi rychle. Avšak při tuhnutí se uvolňuje skupenské teplo, které vznikající směs ohřívá. Jakmile je ohřevem dosaženo teploty tuhnutí, ustanoví se rovnovážný stav a fázová změna ustane.
V případě náhlého tuhnutí vody je množství vzniklého ledu poměrně malé. Snadno to zjistíme jednoduchým výpočtem za použití kalorimetrické rovnice \[\tag{2} m_1 c (t - t_p) = m l_t \] kde m1 je počáteční hmotnost podchlazené vody, m hmotnost ledu, tp teplota podchlazení, lt měrné skupenské teplo tání ledu a t výsledná teplota směsi (tedy teplota tuhnutí). Po dosazení a výpočtu dostaneme, že na každý stupeň Celsia podchlazení je ve vzniklé směsi asi 1,2 % ledu. J. Verne se tedy mýlil, pokud popisoval zamrzání galického moře doprovázené silným praskotem. Ve skutečnosti vzniká jen velmi řídká ledová tříšť, nikoliv masivní led, a žádné praskavé zvuky při tom nelze očekávat.
Měření množství vzniklého ledu představuje zajímavý experimentální problém. Při běžných pokusech je ledu jen velmi málo, je řídce rozptýlen ve vodě a nelze jej od kapalné vody jednoduše oddělit. Jemná ledová tříšť navíc za obvyklé laboratorní teploty rychle taje a samozřejmě i směs vody s ledem při manipulaci přijímá teplo z okolí. Byly vyzkoušeny dvě nepřímé metody měření množství ledu.
Kalorimetrická metoda
Po ukončení tuhnutí co nejrychleji přelijeme obsah nádoby – PET láhve – do kalorimetru a za stálého míchání doléváme teplou vodu až do té doby, než se led rozpustí. Pro rozpuštění platí kalorimetrická rovnice ve tvaru \[\tag{3} m_2 c (t_2 - t) = m l_t + m_1 c t , \] kde m2 je hmotnost teplé vody, t2 teplota teplé vody a t výsledná teplota směsi (očekávána těsně nad 0 °C). Pro omezení vlivu tepelných ztrát či zisků je výhodné volit teplotu teplé vody shodnou s teplotou místnosti a nádobu kalorimetru, ve které ke smíchání dojde, předem pomocí směsi vody a ledu vychladit na 0 °C. Za této podmínky nemusíme v rovnici počítat s kapacitou kalorimetru. Množství použité teplé vody zjistíme nejsnáze tak, že zvážíme nádobu s teplou vodou před a po experimentu.
Měření změny objemu při tuhnutí
Tento experiment je náročnější jak na přípravu, tak i na vlastní provedení. Základní myšlenka vychází ze známého faktu, že led má menší hustotu než kapalná voda a pří částečném ztuhnutí proto dojde ke zvětšení celkového objemu směsi. Vzhledem k tomu, že ledu vznikají řádově jen procenta a hustota ledu se od vody liší o méně než 10 %, je celková změna objemu menší než 1 %. Je tedy zřejmé, že v tomto případě musíme realizovat jemný a citlivý experiment.
Změnu objemu měříme z posuvu krátkého vodního sloupce ve skleněné trubičce, kterou hadičkou spojíme s hermeticky uzavřeným vnitřkem PET láhve. Objemovou kalibraci skleněné trubičky nejsnáze provedeme citlivým zvážením prázdné trubičky a trubičky naplněné vodou. Protože tuhnutí nejsnáze iniciujeme úderem, je dobré mezi měřící trubičku a láhev vložit skleněnou kapiláru, která odstíní prudké změny tlaku při úderu a ochrání měřicí vodní sloupec před roztržením. Současně můžeme měřit i teplotu v láhvi, například termočlánkem umístěným do zdola zatavené skleněné trubičky, kterou přes víčko vzduchotěsně vsuneme do láhve. Vyvarujeme se tak přímému kontaktu podchlazené vody s teplotním čidlem, který snižuje pravděpodobnost, že se nám podaří dosáhnout většího podchlazení.
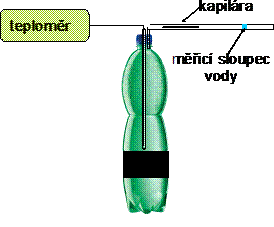
Obr. 2
Pro objem podchlazené vody VV a směsi vody s ledem VS platí vztahy: \[\tag{4} V_V = \frac{m_1}{\rho_V} , V_S = \frac{m_1 - m}{\rho_V} + \frac{m}{\rho_L} , \] kde ρV je měrná hmotnost kapalné vody a ρL měrná hmotnost ledu. Odtud dostaneme vztah pro neznámou hmotnost ledu m \[\tag{5} m=\frac{(V_S-V_V)\rho_L \rho_V}{\rho_V - \rho_L} . \]
Je zřejmé, že experimentální výsledky jsou zatíženy systematickými chybami. Při práci za běžné pokojové teploty se nelze vyhnout ohřívání chladné směsi během manipulace, které systematicky snižuje naměřenou hmotnost ledu. Největší vliv bude mít pravděpodobně ohřev vzduchu v trubičce, kterou měříme objemovou změnu. Tuto chybu lze částečně korigovat následujícím způsobem:
Předpokládejme, že při vzrůstu objemu při tuhnutí je z láhve vytlačován vzduch, který má počáteční teplotu rovnu teplotě podchlazené vody. Ve spojovací hadičce je tento vzduch ohřát na teplotu okolí. Změnu objemu ΔV spojenou s tímto ohřátím určíme ze stavové rovnice pro izobarický děj \[\tag{6} \Delta V = \frac{t_2 - t_p}{T} (V_S - V_V), \] kde T je průměr teplot t2 a tp vyjádřený v kelvinech. Hmotnost ledu pak s touto korekcí určíme jako: \[\tag{7} m = \frac{(V_S - V_V - \Delta V) \rho_L \rho_V}{\rho_V - \rho_L}. \]
Obě dvě výše popsané metody lze použít současně při jednom ztuhnutí, a tak získat dvě zcela nezávisle naměřená čísla umožňující bezprostřední srovnání. Pokud při chlazení vody měříme i teplotu podchlazené vody, získáme třetí nezávislý údaj vypočtený přímo z rovnice .
Výsledky několika experimentů jsou uvedeny v následující tabulce.
| celková hmotnost vody (g) |
podchlazení |
hmotnost ledu (g) | |||
| vypočtená z rovnice |
z kalor. měření |
ze změny objemu | |||
| bez korekce (5) |
s korekcí | ||||
| 500 |
-5,4°C |
34,0 |
34,8 |
37,7 |
34,1 |
| 525 |
-4,7°C |
31,1 |
21,3 |
29,6 |
26,6 |
| 525 |
-4,6°C |
30,5 |
22,3 |
29,6 |
26,6 |
| 1500 |
-3,8°C |
71,9 |
47,7 |
53,2 |
48,2 |
| 1500 |
-5,0°C |
94,6 |
58,8 |
72,8 |
65,1 |
Data v tabulce představují reprezentativní soubor s většího počtu měření, do kterého byly vybrány výsledky z více i méně úspěšných pokusů. Jen s ojedinělými výjimkami je nejvíce odlišná hodnota přímo vypočtená z rovnice . Důvodem je fakt, že teploměr měří teplotu jen v jednom místě láhve, přičemž rozložení teploty určitě není homogenní. Vodou v láhvi však pro dosažení homogenity nelze míchat, aby se předčasně neiniciovalo tuhnutí. Jediný schůdný způsob, jak lépe určit střední hodnotu teploty podchlazené vody, je pravděpodobně měření teploty současně ve více místech. Toto by však úlohu výrazně zkomplikovalo, a proto od tohoto měření bylo upuštěno.
Množství ledu určené ze změny objemu vychází systematicky větší, než kalorimetrické měření. Tento fakt lze, alespoň částečně, vysvětlit tím, že z principu metod je nutné provést kalorimetrický experiment až z jistou prodlevou po určení změny objemu. V této době se směs od okolního vzduchu ohřívá a část ledu předčasně taje.
Korekce na ohřev vzduchu vždy působila správným směrem, což podporuje její oprávněnost.
Praktické poznámky k provedení experimentů
Podchlazenou vodu nejsnáze získáme v zimě, kdy je ranní venkovní teplota kolem ‑5°C. Do čisté vypláchnuté PET láhve nalijeme čistou vodu a necháme venku přes noc. K iniciaci tuhnutí stačí prudčeji lahví bouchnout o zem, případně do ní vhodit malý kousek ledu či sněhu. Autor pro tyto účely používal obyčejnou „brněnskou“ vodu z vodovodu a při mnoha desítkách pokusů bylo dosaženo lepší než 90 % úspěšnosti.
Ve většině případů se však nelze spoléhat na počasí a vodu je nutné vychladit uměle. Bohužel běžné chladničky ani mrazničky k tomuto účelu vhodné nejsou, v chladničce je teplota příliš vysoká a v mrazničce naopak nízká a je tedy vysoká pravděpodobnost že voda spontánně zmrzne. Dobře se osvědčilo chlazení směsí solného roztoku a ledu. Na podchlazení 1,5l PET lahve stačí asi 1kg ledové tříště, kterou smícháme s půl litrem vychlazené vody. Za stálého míchání přidáváme sůl tak, aby teplota směsi klesla na - 8°C až - 9°C. Ledovou tříšť a PET láhev s vodou pak umístíme do dobře tepelně izolované nádoby. Pokud výchozí teplota vody je blízká 0°C, k dostatečnému podchlazení stačí 30 – 60 minut. Je výhodou, máme-li uvnitř láhve zabudován teploměr (viz obr. 2). Pak můžeme kontrolovat teplotu podchlazení a okamžitě také poznáme, pokud nám voda nechtěně zmrzne (teplota rychle stoupne na 0°C, kde dlouho setrvá).
Celý experiment je třeba provést co nejrychleji, pro omezení ohřevu směsi, proto si vše předem pečlivě připravíme. Ne vždy se podaří vylít všechen led z láhve přes její hrdlo a je nutné láhev rychle rozříznout. Velmi důležitým parametrem, který výrazně ovlivní výsledek, výsledná teplota rozpuštěné vody v kalorimetru. Vždy je několik desetin stupně nad nulou, neboť pro urychlení roztátí je lepší nalít do směsi trochu více teplé vody. Pro měření výsledné teploty je třeba použít co nejpřesnější teploměr.
Experiment probíhá tak, že nejprve opatrně vyjmeme láhev z chladící směsi. V té době je láhev již připojena k měřící trubičce. Poznamenáme počáteční polohu vodního sloupce v trubičce. Úderem láhve o stůl iniciujeme tuhnutí a pozorujeme posuv vodního sloupce. Jakmile se zastaví a nebo výrazně zpomalí, poznamenáme jeho konečnou polohu. Nezdržujeme se čtením poloh na stupnici, ale obě polohy jen rychle označíme, například připnutím prádelního kolíčku na měřící trubičku. Co nejrychleji vyprázdníme obsah láhve do kalorimetru předem vychlazeného na 0°C. Za stálého míchání doléváme teplou vodu a pečlivě sledujeme okamžik, až všechen led roztaje. Po celou dobu máme v kalorimetru vložen citlivý teploměr, také předem vychlazený na 0°C, aby změření výsledné teploty směsi proběhlo co nejrychleji. Potřebná experimentální data – posuv vodního sloupce v trubičce a hmotnost použité teplé vody – změříme a zapíšeme až po ukončení experimentu.
Literatura
[1] http://en.wikipedia.org/wiki/Nucleation
[1] Správněji by měl být použit Gibbsův potenciál, jako termodynamický potenciál pří konstantní teplotě a tlaku.
[2] Problém nukleace se neobjevuje pouze u tuhnutí, ale také například při varu a kondenzaci vody z vodní páry. Přehřátá voda nezačne vřít z velmi podobného důvodu, jako podchlazená voda nezačíná tuhnout. Chemikové tomuto stavu říkají utajený var. Protože při práci v chemické laboratoři představuje určité riziko, běžně se utajenému varu zabrání použitím tzv. varného kamínku, který vlastně zajistí heterogenní nukleaci bublinek páry.