O příspěvku
PDF ke staženíLeslieho kostka a Ritchieho pokus
Anotace
Osvěžení zákonů vyzařování a sestavení dvou polozapomenutých pokusů s dlouhovlnným infračerveným zářením – sáláním.
Úvod
Infračervené záření objevil F. W. Herschel známým pokusem. Hranolem rozložil sluneční světlo na spektrum a do barevných pásů přikládal teploměr. Směrem k červené oblasti spektra teplota rostla. Dokonce za červenou teplota stoupla více než v kterékoliv části viditelného spektra. Tak objevil infračervené záření. Tento pokus má v sobě skrytý problém. Hranol roztahuje kratší vlnové délky na větší kus stínítka, kdežto červené a zejména infračervené záření zůstává mnohem koncentrovanější. Největší „díl energie slunce“ je mezi žlutou a zelenou, kdežto ve výše zmíněném uspořádání se zdají jeho tepelné účinky být největší až za červeným koncem. Kdybychom místo hranolu použili spektrální mřížku, nebo v korekci vzali v úvahu proměnnou schopnost hranolu lámat světlo různých vlnových délek, pozorovali bychom v IR oblasti dokonce pokles teploty. Herschelův objev IR záření byl tudíž výsledkem shody okolností. Dlouholeté úsilí o formulaci zákonů vyzařování těles bylo dovršeno známým Planckovým zákonem o záření absolutně černého tělesa (AČT).
Všechna tělesa však emitují při stejné teplotě méně energie než AČT. Koeficient vyjadřující vztah mezi skutečnou vyzařovanou energií a energií vyzařovanou AČT stejné teploty je znám jako emisivita. Hodnota emisivity určena povrchovými vlastnostmi tělesa.
Pro viditelné světlo i pro IR platí, že čím je povrch materiálu více vyleštěný, tím více záření odráží. Skutečnou energii vyzařovanou nečerným tělesem získáme jako součin energie AČT při téže teplotě (z Planckovy křivky) a spektrální emisivity (z tabulek nebo měření) v oboru vlnových délek našeho zájmu. Tělesa s emisivitou závislou na vlnové délce nazýváme selektivní.
Tedy emisivita je mírou schopnosti daného předmětu vyzařovat infračervenou energii. Emisivita může nabývat hodnot od 0 (zcela lesklé zrcadlo) do 1,0 (černé těleso). Většina organických, nabarvených nebo zoxidovaných povrchů má emisivitu blízkou hodnotě 0,95. Některé jednodušší teploměry mají emisivitu pevně nastavenou na tuto hodnotu. Dokonalejší přístroje disponují možností uživatelského nastavení emisivity. Jestliže potřebujeme měřit lesklý předmět (IR teploměrem s nastavenou emisivitou 0,95), ošetříme jeho povrch matnou černou barvou a měříme na tomto upraveném místě.
Tělesa přijímají IR záření od okolních těles, z termodynamických úvah víme, že těleso pohlcuje nejsilněji právě ty spektrální složky záření, které samo nejsilněji vyzařuje a naopak. Toto tvrzení označujeme jako Kirchhoffův zákon.
Tedy při dané teplotě těleso tím více vyzařuje, čím větší má absorpční schopnost. Pokud je absorpční schopnost široká a velká, těleso se jeví černé, byť v optickém spektru má jinou barvu.
Pokus 1
V experimentu bude užita tzv. Leslieho kostka. Je to asi litrová kovová kostka s různě ošetřenými povrchy. Jeden stěna je bílá, druhá černá, třetí kovově lesklá, čtvrtá třeba oranžová.
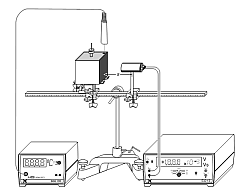
Kostka se naplní horkou vodou o teplotě asi 90°C a pomocí sestavy „termočlánků“ od firmy Leybold budeme měřit tepelný tok z různých stěn kostky při chladnutí kostky.
Výstupní napětí termočlánkového pole bude úměrné příslušným teplotám a celkovým vyzařovaným tepelným tokům. Vzhledem k tomu, že měřený objekt – kostka může také absorbovat a reflektovat teplotní záření z okolí, které má obvykle jinou teplotu T0, bude výsledný celkový vyzařovaný tok počítán z rovnice:
\[ M' = \varepsilon \cdot \delta \cdot (T^4 - T_0^4) .\] 
Obr. 1
Obr. 2
Z grafu měření je vidět, že bílý i černý povrch v oblasti běžných teplot kolem 7 μm jsou skoro identické.
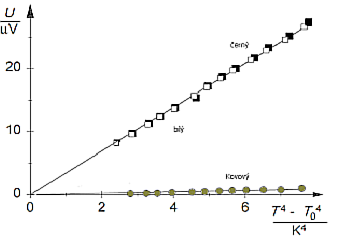
Graf 1
Pokus 2
Dalším pokusem je Ritchieho pokus, jímž byl experimentálně prokázán Kirchhoffův zákon vyzařování. K pokusu potřebujeme kromě Leslieho kostky ještě nějaké zařízení, které by fungovalo jako diferenciální teploměr.

Obr. 3
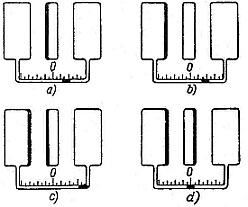
Obr. 4
Lesklý kovový kotouč má stálou vyšší teplotu než okolí. Na obou stranách kotouče jsou souměrně dva lesklé kovové válce uvnitř s vzduchotěsnou trubičkou a kapalinovou značkou v kapiláře uprostřed – indikační diferenciální teploměr. Zakryjeme-li levou stranu černým povlakem, pozorujeme posuv kapalinové značky doprava případ a). Značka se nehýbe, přeneseme-li černý povrch na levý váleček indikátoru b). Pokryjeme-li obě protilehlé levé strany černým povrchem současně, značka se vzdálí ještě více ke kraji c). Otočíme-li nyní kotouč zářiče o 180°, vrátí se značka po chvíli do středové polohy d).
Z výsledků pokusu plyne, že černá plocha září při stejné teplotě více než lesklá a že také více pohlcuje. Z posledního případu pak soudíme, že množství tepla, které si střední kotouč – zářič vyměňuje s oběma válci, musí být stejné. Za jistou dobu se ustaví rovnováha a všechny plochy budou na stejné teplotě. Tedy označíme-li EL, AL jako emisivitu a pohltivost lesklého povrchu a EČ, AČ jako adekvátní veličiny pro černý povrch je výsledek pokusu vyjádřen vztahem: \[ E_L \cdot A_{\check{C}} = E_{\check{C}} \cdot A_{L} .\]
Z toho plyne, že podíl \( \frac{E_L}{A_L} = \frac{E_{\check{C}}}{A_{\check{C}}} = f(T,\lambda) \) má pro danou teplotu a danou vlnovou délku stálou hodnotu pro nejrůznější tělesa.

Obr. 5
Diferenciální teploměr lze vytvořit z injekčních stříkaček, upravených víček na zavařeniny hadičky, kapiláry a obarvené kapaliny (voda+líh). Jako zářič s jedním povrchem černým a druhým kovově lesklým byl použit rajský protlak, který lze v troubě zahřát i mírně nad 100 °C, aniž by se výrazně deformoval.

Obr. 6
Literatura
[1] Levitin I. B.: Infračervená technika, ALFA – Bratislava 1973
[2] What is a Blackbody and Infrared Radiation? http://www.electro-optical.com