O příspěvku
PDF ke staženíVybrané experimenty v rotujících soustavách
Příspěvek popisuje několik netradičních experimentů v rotujících soustavách. Jedná se především o různé modifikace pokusu s kónickým kyvadlem. Je nastíněno jak jejich teoretické odvození, tak praktické provedení. Na střední škole bývá často jako příklad setrvačné odstředivé síly uváděn řetízkový kolotoč. Následujících několik experimentů souvisí právě s ním.
Kónické kyvadlo (teorie)
S výpočtem kónického kyvadla se setkal snad každý, kdo prošel vysokoškolským kurzem. Problému kónického kyvadla je věnována řada publikací (např. [1], [2]).
Jednoduché kónické kyvadlo (kulička na závěsu)
Kónickým kyvadlem rozumíme hmotný bod o hmotnosti m upevněný na konci tuhého přímého vlákna konstantní délky l, jehož hmotnost je zanedbatelná a jehož druhý konec je upevněn v pevném bodě. Kónické kyvadlo se narozdíl od matematického kyvadla pohybuje tak, že koná rovnoměrný pohyb po kružnici ve vodorovné rovině.
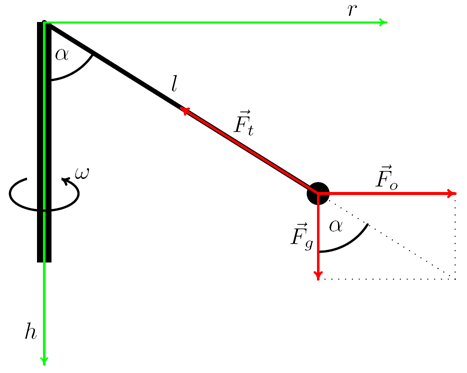
Obr. 1: K odvození výchylky kónického kyvadla
Z geometrie situace na obr. 1 plyne, že \[ \mathrm{tg}\,\alpha = \frac{F_o}{F_g} = \frac{m \cdot \omega^2 \cdot r}{m \cdot g} = \frac{\omega^2 \cdot r}{g} = \frac{\omega^2 }{g} \cdot l \cdot \sin \alpha .\] Vztah lze dále upravovat na \[ 0 = \left(\frac{\omega^2}{g} \cdot l - \frac{1}{\cos \alpha} \right).\] Odtud plyne, že jeden z čitatelů musí být roven nule. Tzn. \( \cos \alpha = \frac{\omega^2}{g}\cdot\frac{1}{l}\) nebo \( \sin \alpha = 0 \). První rovnost bude splněna pouze v případě, že \( |\frac{\omega^2}{g}\cdot\frac{1}{l}|\leq1 \), v opačném případě bude platit druhá rovnost. Definujme proto \( \omega_0 = \sqrt{\frac{g}{l}}\). Pro odklon závěsu hmotného bodu v závislosti na počátečních podmínkách tak dostáváme následující vztahy: \[\tag{1}\mathrm{pro} \omega < \omega_0\ :\ \alpha = 0 ,\] \[\tag{2}\mathrm{pro} \omega \geq \omega_0\ :\ \alpha = \arccos \left(\frac{\omega^2}{g}\cdot\frac{1}{l}\right) .\]
Je tedy patrné, že pokud začneme takovým zařízením otáčet, měla by být výchylka nulová až do okamžiku, kdy úhlová rychlost přesáhne hodnotu ω0. Graf takové závislosti je vynesen na obr. 2.
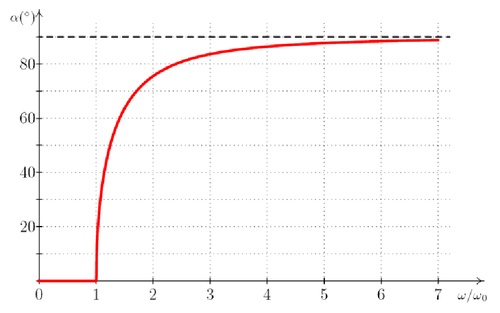
Obr. 2: Závislost výchylky kónického kyvadla na parametrech experimentu (na \(\frac{\omega}{\omega_0}\))
Složitější kónické kyvadlo (více kuliček zavěšených pod sebou)
Jednoduché kónické kyvadlo zřejmě nikoho neohromí. Proto se zkusme ptát, co se stane, pokud podobných kónických kyvadel pověsíme více pod sebe (více kuliček zavěšených pod sebou). Situace s jejich různým počtem zachycuje obr. 3. a 4.
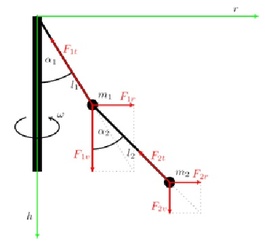
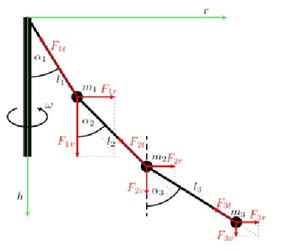
Obr. 3: Znázornění situace pro dvě a více kuliček zavěšených pod sebou
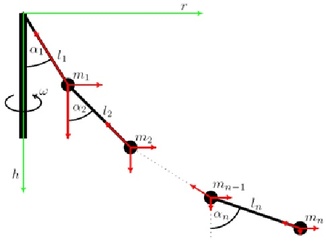
Obr. 4: Znázornění situace pro více kuliček zavěšených pod sebou
Obdobným způsobem jako u kónického kyvadla i zde lze odvodit vztah pro výchylku závěsu libovolné kuličky od svislého směru. Opět se ukazuje, že až do jisté úhlové rychlosti ω0, je výchylka všech závěsů v daných případech nulová. ω0 pak definujeme jako \[\tag{3} \omega_0 = \sqrt{\frac{g}{l_1+l_2+...+l_n}}\] kde n je počet kuliček v daném případě.
Vztahy pro jednotlivé výchylky však již nelze řešit analyticky, nýbrž je nutné použít jednu z iteračních metod. Ukazuje se, že metoda prosté iterace je naprosto dostačující. Při velkém množství zavěšených kuliček (hmotných bodů) a krátkých závěsech dostáváme dobrou představu o tom, jak se bude při otáčení chovat řetízek či provázek připevněný k ose rotace.
Olovnice v rotující soustavě (řetízkový kolotoč)
Věrněji než kónickým kyvadlem můžeme řetízkový kolotoč modelovat tak, že tuhé přímé vlákno neupevníme přímo k ose rotace, nýbrž na raménko nenulové délky (viz obr. 5).
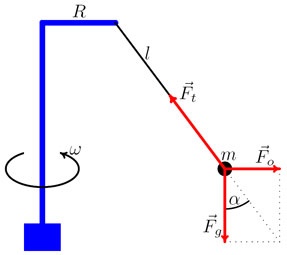

Obr. 5: K odvození výchylky olovnice v rotující soustavě
Z obrázku 5 je patrné, že \[ \mathrm{tg}\, \alpha = \frac{F_o}{F_g} = \frac{m \cdot \omega^2 \cdot (R+l \cdot \sin \alpha)}{m \cdot g} = \frac{\omega^2 \cdot (R+l \cdot \sin \alpha)}{g} = \frac{\omega^2 }{g} \cdot (R+l \cdot \sin \alpha) .\] Je zřejmé, že tento vztah nebude možné řešit analyticky. Nejsnazší cestou vedoucí k cíli se ukázala být opět metoda prosté iterace vztahu \[ \alpha = \mathrm{arctg}\,\frac{\omega^2 }{g} \cdot (R+l \cdot \sin \alpha) .\] Pomocí některého tabulkového procesoru (např. MS Excel) tak snadno ověříme měřené hodnoty. Ani zde výchylka nezávisí na hmotnosti závaží. Rozdíl oproti kónickému kyvadlu je, že nyní je výchylka α rovna nule pouze při nulové úhlové rychlosti (viz obr. 8).
Praktická část (experimentální ověření)
Pro pokusy byl použit motor z vybavení KDF MFF UK. Na motoru je upevněna hliníková tyčka o průměru 8 mm a délce 447 mm. Na vrcholu osy je umístěno ramínko, které slouží pro připevnění bifilárního závěsu kónického kyvadla, případně prvního závaží (viz obr. 5). Aby bylo možné závěs upevnit i v nenulové vzdálenosti od osy rotace bylo ke stávajícímu raménku připevněno další (viz obr. 6). Hmotné body je v experimentu možno nahradit matičkami, které se navíc dobře uchycují na provázek.

Obr. 6: Složitější kónické kyvadlo
Pro odečítání výchylek provázků jsem použil kameru, která byla umístěna vně rotující soustavy. Záznam byl pořízen po částech, vždy krátký snímek o délce několik sekund pro danou frekvenci otáčení, délku závěsu a závaží.
Videozáznam jsem převedl pomocí programu Windows Movie Maker do počítače. Poté jsem v programu Virtual Dub určil periodu otáčení soustavy a nalezl jednotlivá políčka filmu, ze kterých bylo možné v programu Corel odečíst polohy upevnění závěsů a jednotlivých matiček. Z těchto údajů již bylo snadné určit výchylky jednotlivých závěsů od svislého směru. Pro každé nastavení experimentu (pro stejné matičky, délky vláken, délku ramínka a frekvenci rotace) jsem odečetl hledaný úhel z více vyhovujících políček filmu. Experimentální úhel vynášený do grafů je pak jejich aritmetickým průměrem.
Kónické kyvadlo a jeho rozšíření
U kónického kyvadla je předpoklad, že výchylka nebude záviset na hmotnosti závaží. To potvrzuje i experiment. Jak je vidět z obrázku 7, hodnoty pro tři různé matičky (jsou vyznačeny různými symboly) velmi dobře odpovídají křivce, která byla pro danou délku vlákna určena podle vztahů (1) a (2). Stejně dobře jako u jednoduchého kónického kyvadla odpovídají i hodnoty pro dvě a tři matičky zavěšené pod sebou. Odchylka teoretických hodnot úhlů od experimentálních je v průměru 0,59 %. Pro jednotlivé frekvence je pak maximálně 6,2 %.

Obr. 7: Model řetízkového kolotoče

Obr. 8: Graf závislosti výchylky závěsu na frekvenci otáčení pro matici na závěsu o délce l = 193 mm. Do grafu jsou vyneseny experimentálně získané hodnoty pro tři matice o různých hmotnostech.
Je zřejmé, že experiment pro více kuliček bychom proměřovali jen velmi těžko. Ale při výpočtu případu pro n závaží se ukazuje, že každá kulička je vychýlena více než předchozí. To lze jednoduše kvalitativně demonstrovat (viz obrázek 9).

Obr. 9: Rotující závěs osmi kuliček. Několik snímků při různé úhlové rychlosti otáčení.
Model řetízkového kolotoče
Z obrázku 10 je patrné, že experimentálně získané hodnoty výchylky závěsu modelu řetízkového kolotoče dobře odpovídají teoretické závislosti (křivce), která byla proložena body získanými pro danou situaci iteracemi příslušného vzorce. Odchylka teoretických od naměřených hodnot je v průměru 1,7 %, maximálně však přibližně 6 %.
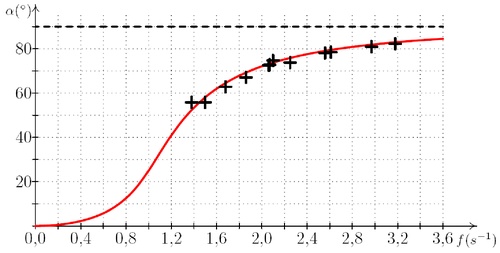
Obr. 10: Graf závislosti výchylky závěsu na frekvenci otáčení pro matici na závěsu o délce l = 144 mm upevněném na ramínku délky R = 55 mm.
Závěr
Při podobných experimentech jako byly vyloženy zde, si studenti procvičí nejen znalosti z fyziky a matematiky, ale také si důkladně osvojí práci s počítačem a kamerou. Právě díky využití multimediální techniky se pro studenty mohou jevit jako velmi atraktivní. Obtížnost výpočtů a časová náročnost je však předurčuje pro použití spíše ve fyzikálním semináři na střední škole. Pevně věřím, že předložené náměty se stanou inspirací pro nejednoho pedagoga.
Všechny nastíněné pokusy jsou součástí diplomové práce autora s názvem Experimenty pro interaktivní fyzikální laboratoř: vybrané experimenty v rotujících soustavách, kde jsou také mnohem podrobněji popsány. Tato diplomová práce je dostupná i na webových stránkách [3].
Literatura
[1] SUTTON, Richard Manliffe. Demonstration Experiment in Physics. USA: American Association in Physics, 2003. 545s. Poprvé vydáno roku 1938 nakladatelstvím McGraw-Hill Book Company. Dostupný z WWW: <http://physicslearning.colorado.edu/PiraHome/Sutton/Sutton.htm>. [cit. 21. 11. 2007]. ISBN 1-931024-05-7.
[2] PROCTOR, Ivan, EDWARDS, T. H. Conical Pendulum Experiment. American Journal of Physics . June 1968, vol. 36, is. 6, s. 555-556.
[3] www.sabatka.webz.cz/diplomka [cit. 21. 8. 2008]