Pokusy na Malé Hraštici – tentokrát s teplem
Příspěvek popisuje: 1) Jednoduchou demonstraci adiabatického děje, resp. rozdílu mezi adiabatickým a izotermickým dějem, dokonce s možností přibližně určit velikost Poissonovy konstanty \( \kappa \cdot \left(\frac{C_p}{C_V} \right)\). 2) Skupinu pokusů na demonstraci a měření přenosu tepla zářením, a to jak pomocí prostředků ICT („dataloggeru“), tak jednoduchými pomůckami za pár korun.
Úvod – oč jde na Malé Hraštici
Jarní soustředění pro budoucí učitele fyziky a „spřízněné duše“ se konají již od roku 1997. Tradičně je pořádáme začátkem května v táborové základně u vesničky Malá Hraštici nedaleko Dobříše. Soustředění trvá 4–5 dní a účastní se ho asi 15–25 účastníků. Většinou jde o posluchače učitelství fyziky z naší fakulty včetně doktorandů, ale přijíždějí i absolventi, kteří už učí na školách a občas i další hosté.
Soustředění je velice neformální a zcela dobrovolné. Studenti za účast nedostávají žádné kredity ani nic jiného. Na Hraštici se prostě jezdíme bavit fyzikou. A také (protože nejen fyzikou živ je člověk) mimoodborným programem, který je se soustředěním neodmyslitelně spjat. Odborná část programu se převážně realizuje formou miniprojektů. Dvojice, trojice či libovolné skupinky účastníků si prostě vyberou témata, která je zaujmou a zkoušejí v nich něco „vybádat“. Samozřejmě nejde o objevování nějaké „nové fyziky“, ale o to, vyzkoušet si nějaký pokus, vymyslet jeho novou variantu nebo zkusit něco naměřit. A udělat to ne v prostředí školního praktika či vědecké laboratoře, ale doslova „v polních podmínkách“, kde musíme improvizovat, využívat jednoduché materiály a hledat nestandardní řešení. Že to trénuje kreativitu, fyzikální cit a nejrůznější dovednosti, je jasné. Výsledky si pak účastníci neformálně prezentují. Výsledkem přitom může být, stejně jako ve skutečném vědeckém výzkumu, i negativní zjištění typu „tudy cesta nevede“, „je to složitější, než jsem si myslel“, případně „na tohle se ještě budeme muset pořádně podívat“.
Podrobnosti o soustředění a miniprojektech mohou zájemci najít v článku [1]. Zde bych chtěl upozornit na jeden důležitý aspekt: soustředění umožňuje vyzkoušet si spoustu věcí a přináší nápady a inspiraci pro nové pokusy či jejich varianty a nové jednoduché přístroje a pomůcky. Řada námětů, které vznikly či byly prvně odzkoušeny právě na Malé Hraštici, již byla publikována i ve sbornících Veletrhu nápadů, viz např. [2], [3].
V roce 2008 bylo hlavním tématem odborného programu Teplo. V dalším textu popíšu dva příklady pokusů, které jsem si tam vyzkoušel.
Adiabatický a izotermický děj v malém a názorně
Izotermický a zejména adiabatický děj se ve středoškolské fyzice často zavádějí jen teoreticky. Následující jednoduchý pokus umožňuje jednoduše demonstrovat jejich rozdíl – a dokonce přibližně určit i velikost Poissonovy konstanty κ.
Princip pokusu ukazují obrázky 1 a 2. Hrdlem láhve prochází trubička, v ní je několikacentimetrový sloupec vody. V láhvi je vzduch. Je-li trubička vodorovně (obrázek 1), je v láhvi atmosférický tlak.
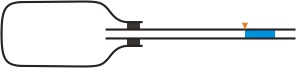
Obr. 1: Je-li trubička vodorovně, je v láhvi stejný tlak, jako v okolní atmosféře
Otočíme-li láhev s trubičkou do svislé polohy (obrázek 2), zvýší se tlak v láhvi o hydrostatický tlak daný výškou vodního sloupce. Vzduch v láhvi se trochu stlačí a sloupeček vody se posune níž.
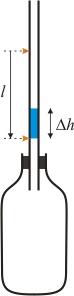
Obr. 2: Ve svislé poloze se v láhvi tlak zvýší
A kde je slibovaný rozdíl mezi izotermickým a adiabatickým dějem?
Provedeme-li pokus, hned to uvidíme:
Sloupec vody nejprve rychle „spadne“ o určitý kus a pak pomaleji „dobíhá“.
To úvodní „spadnutí“, tedy úvodní stlačení vzduchu v láhvi, je děj tak rychlý, že se při něm teplota vzduchu v láhvi ještě nestačí vyrovnat s okolím. Probíhá tedy stejně, jako by vzduch v láhvi byl tepelně izolován – to znamená, že jde o děj adiabatický. Při něm tlak při stlačování roste rychleji, než by to bylo při ději izotermickém. Proto stačí menší stlačení (menší pokles sloupečku vody) k tomu, aby přetlak v láhvi daný sloupec vody udržel. Vzduch v láhvi se přitom trochu zahřeje, ale to v pokusu nijak neměříme ani neucítíme.
Teplota vzduchu se ovšem během několika následujících sekund vyrovná s okolím, takže je stejná jako na začátku. Proto pro výsledný objem vzduchu v láhvi můžeme použít známý vztah pro izotermický děj: p·V = konst. Ale i bez počítání, z „fyzikálního názoru“, je jasné, že když vzduch v láhvi zase zchladl, jeho objem se zmenší a sloupeček vody v trubičce se tedy posune dolů.
Trocha kvantitativních odhadů a výpočtů
Začněme izotermickým dějem. Ze vztahu p·V = konst. by šlo „vysokoškolským způsobem“ pomocí derivování resp. diferenciálů odvodit pro změnu objemu vztah \( \Delta V \dot{=} -\frac{V}{p} \Delta p \). Ale zkusme to jednodušeji, otázkou, kterou lze položit i žákům: Jestliže stoupne tlak p o 1 %, o kolik musí klesnout objem V, aby zůstal součin p·V konstantní?
Jistě, objem musí klesnout také asi o 1 %. (Ať už o tomhle žáky přesvědčíte tím, že si na kalkulačce vydělí 1 číslem 1,01 nebo vynásobí čísla 1,01 a 0,99 nebo jinak. Je asi dobře žáky upozornit, že tohle platí jen pro malé změny tlaku, tedy že při zvýšení tlaku o 200 procent rozhodně objem o 200 procent neklesne.)
Přírůstek tlaku o 1 % nastane pro vodní sloupec vysoký 10 cm. (Buď jej můžeme spočíst pomocí vztahu Δp = Δh·ρ·g, nebo žákům připomeneme, že 10 cm je setina z 10 m, tedy z výšky vodního sloupce, kterou „unese“ atmosférický tlak.) Má-li láhev objem 0,5 l a trubička má vnitřní průměr 4,4 mm (tedy plocha jejího vnitřního průřezu je asi 0,15 cm2), odpovídá změně objemu o 1 % posun sloupečku vody asi o 33 cm. Pro sloupec vody dlouhý jen 5 cm bude změna tlaku i objemu jen půl procenta, sloupec vody tedy klesne jen o necelých 17 cm. A tak dále.
Jak je tomu pro adiabatický děj? Nyní platí p·Vκ = konst. Vzrůstu tlaku o 1 % teď neodpovídá pokles objemu o celé procento, ale o méně: jen o 1/κ %. Pro κ = 1,4 tedy objem poklesne jen asi o 0,7 %. I tohle můžeme jednoduše ilustrovat výpočtem na kalkulačce: zkuste vynásobit 1,01·0,9931,4. (Samozřejmě, v semináři se středoškoláky, kteří již ovládají derivování, by šlo odvodit i obecný vzorec \( \Delta V \dot{=} -\frac{V}{\kappa \cdot p} \Delta p \) .)
Pro výše zmíněný příklad půllitrové láhve a trubičky s průměrem 4,4 mm vyjde pokles deseticentimetrového sloupce vody jen necelých 24 cm; pro poloviční sloupec je pokles samozřejmě také poloviční.
Důležité je, že poměr délek, o něž se sloupec posune při izotermickém ději (lI) a při adiabatickém ději (lA) je roven Poissonově konstantě κ: \[ \frac{l_I}{l_A} = \kappa \]
Je to vidět jak z uvedeného příkladu, tak ze zmíněných obecných vztahů.
Provedení pokusu
Pokus lze udělat s těmi nejjednoduššími pomůckami. Místo skleněné trubičky můžeme použít plastovou hadičku s prodejen potřeb pro zahrádkáře. Její vnitřní průměr je výše uvažovaných 4,4 mm. Hadička jde nasadit na „hrot“ plastové injekční stříkačky. Uříznutou stříkačku 20 ml lze těsně vsunout do hrdla plastové láhve. K hadičce přilepíme kus papírového měřítka – a můžeme začít měřit. Jedna „technická rada“: při změně polohy hadičky z vodorovné do svislé je vhodné ucpat konec hadičky prstem. Sloupec vody pak drží na původním místě; klesat začne, až uvolníme prst.

Obr. 3: Provedení pokusu
Měření je samozřejmě spíše orientační. Voda v hadičce má občas tendenci „zadrhávat“ (je vhodné na hadičku trochu poklepat), polohu sloupce vody odpovídající rychlému prvnímu poklesu (tedy hodnotu lA) je těžké přesně odečíst atd. Přesto výsledky dávají hodnotu Poissonovy konstanty v okolí 1,4 (což je tabulková hodnota pro vzduch).
Ještě jedno upozornění: plastovou láhev neberte při měření do ruky. Ohřeje-li se láhev teplem ruky, vzduch se v ní rozpíná a z celého zařízení máme spíše „termoskop“, než přístroj na měření κ.
Přenos tepla zářením
Demonstraci přenosu tepla zářením byla na Veletrhu nápadů věnována již řada příspěvků. Což takhle šíření tepla zářením – třeba ze Slunce, ale nejen z něj – i kvantitativně změřit? A to s jednoduchými pomůckami a pokud možno rychle.
Na Hraštici nám pomohl LabQuest firmy Vernier (viz např. [4]) s malou sondou pro měření teploty. LabQuest je malé „ruční“ zařízení pro počítačový sběr dat s experimentu, jehož výhodou je, že je lze vzít třeba ven na louku nebo využít v „polních podmínkách“ na soustředění typu Hraštice. Přesně to jsme udělali. Sondu pro měření teploty jsem přilepil izolepou ke kousku měděného plechu (5x5 cm), který jsem z jedné strany nastříkal černým lakem ze spreje. Plech byl z druhé strany izolován pěnovým polystyrénem. (Byl do něj poněkud „zapuštěn“, což jde udělat, když ho nahřejeme páječkou – samozřejmě ještě před přilepením sondy.)
Když začerněný plech vystavíme slunečnímu záření, rychle se ohřívá. LabQuest nahrává data (standardně po každé polovině sekundy), umí je zobrazit v grafu a proložit částí grafu lineární závislost – tedy spočíst, jak teplota stoupá s časem, viz obrázek 4.
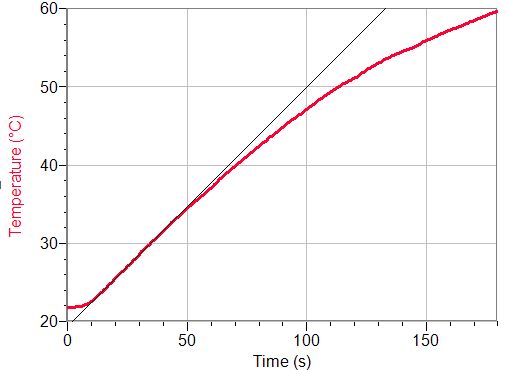
Obr. 4: Nárůst teploty začerněného měděného plíšku zahřívaného slunečním zářením
Při vyšších teplotách samozřejmě teplota stoupá pomaleji (plech je ochlazován například okolním vzduchem), ovšem zpočátku stoupá teplota prakticky lineárně – v našem případě asi o 0,30 až 0,33 K·s-1. Z tepelné kapacity plechu (tu určíme z hmotnosti a specifické tepelné kapacity mědi) vychází, že plíšek byl ohříván příkonem asi 1,5 W. Po přepočtu na metr čtvereční dostáváme 600 W·m-2. To je sice méně než solární konstanta (i než intenzita slunečního záření uváděná na povrchu Země, která má činit asi 1 kW·m-2), ale řádově se obě hodnoty shodují a rozdíl lze vysvětlit ztrátami tepla i tím, že v době měření nebyla úplně jasná obloha.
Začerněný plech můžeme zahřívat i jinými zdroji záření, například:
• Stolní lampou.
• Plechovkou, naplněnou horkou vodou. (Plechovku či její část ovšem nenecháme lesklou, ale také ji nastříkáme černou barvou.)
• Vlastní dlaní. V tomto případě samozřejmě roste teplota pomaleji – ale kupodivu jen asi desetkrát pomaleji než při ohřívání Sluncem. Počáteční nárůst činil 0,03 K·s-1 (při vzdálenosti dlaně 2 cm). Pokud místo měděného plechu použijeme začerněnou hliníkovou fólii, je počáteční rychlost nárůstu teploty až 0,14 K·s-1.
Jak měřit stokrát laciněji
Čtenář se možná poněkud rozčílil, že jsem výše mluvil o jednoduchých pomůckách a vzápětí o měření pomocí LabQuestu, což je zařízení v ceně kolem deseti tisíc korun. Takže se podívejme, jak to udělat laciněji, pomocí běžného multimetru.
Máme-li multimetr se sondou k měření teploty, můžeme ji využít – ovšem přesnost měření je jen na celé stupně. Druhou možností je použít perličkový termistor (v ceně řádově deset Kč) a multimetrem měřit jeho odpor. Teplotní závislost ovšem musíme předem proměřit (tedy provést kalibraci). S pomocí baterie a několika rezistorů lze dosáhnout toho, aby multimetr zapojený jako měřič napětí ukazoval údaj, který s teplotou stoupá a dokonce (alespoň přibližně) číselně odpovídá měřené teplotě. Ale podrobnosti už se do tohoto článku nevejdou – snad tedy někdy příště.
Literatura
[1] Dvořák L.: Labs outside labs: miniprojects at a spring camp for future physics teachers. European Journal of Physics 28 (2007), S95–S104.
[2] Dvořák L.: Trocha heuristiky z Malé Hraštici. In: Sborník konference Veletrh nápadů učitelů fyziky 5. Ed.: Rauner K., ZČU Plzeň 2001, s.143–146.
[3] Dvořák L.: Netradiční měřicí přístroje 4: Měření krátkých časů. In: Sborník konference Veletrh nápadů učitelů fyziky 9, svazek I, Ed. Smetanová J., Sládek P., Paido 2004, s. 30–32.
[4] Pazdera V.: LabQuest – měření v terénu. Příspěvek v tomto sborníku.