Dva jednoduché inovační pokusy z mechaniky
Úvod
Pokus ve vyučování fyzice má stejný význam jako ve fyzice, tzn. je verifikátorem pravdivosti výsledku úvah nebo východiskem k bádání o dosud neznámých jevech. Následující dvě ukázky mají zdůraznit význam pokusu ve vyučování fyzice zejména pro rozvíjení fyzikálního myšlení žáků. To se nerozvíjí při pouhém sledování pokusu (pozorování), ale až tehdy, když se žák snaží nalézt odpověď na otázku PROČ k jevu dochází.
1 Kapalina v nádobě (problémové úlohy)
Pokus má žáky přesvědčit, že pro kapalinu v klidu platí Pascalův zákon a že příčina pohybu kapaliny je způsoben rozdílem tlaků. Z didaktického hlediska není vždy dobré předem žákům sdělovat, co chceme pokusem dokázat.
Pro splnění shora uvedeného záměru se mi osvědčil následující postup, při kterém žáci nejdříve zdůvodňovali odpovědi na pokládané otázky (PROČ?) a následující pokusy prokázaly, které odpovědi byly správné.
Pomůcky:
PET láhve, větší vanička, kádinka, nálevka, délkové měřidlo, jehlice s ostrým hrotem (na dělání otvorů v láhvích), odměrný válec, stopky, kontaktní měřidlo.
P1 Prázdná láhev ve vodě
O1 Co se stane, když ponoříme prázdnou láhev se dvěma otvory (A, B) do vody podle obr. 1?

Obr.1
(Voda stříká otvory dovnitř láhve. PROČ?
Kapalina působí tlakovou silou vždy kolmo ke stěně nádoby. F = pS)
P2 Láhev naplněná vodou a uzavřená
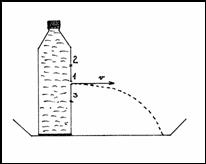
Obr. 2
O2 Co se stane, když uděláme otvor 1 ve stěně láhve – obr. 2.
(Voda neteče. PROČ?)
O3 Co se stane, když láhev stlačíme?
(Voda stříká. PROČ? – Pascalův zákon)
O4 Co se stane, když uděláme druhý otvor 2 nad prvním otvorem?
(Voda stříká jen ze spodního otvoru. PROČ? )
O5 Co se stane, když uděláme třetí otvor 3 pod prvním otvorem?
(Voda stříká jen z tohoto otvoru. PROČ? )
P3 Láhev naplněná vodou – nejdříve zavřená, potom otevřená
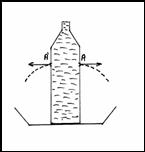
Obr.3
Láhev naplníme vodou a uzavřeme. Uděláme otvor A. Už víme, že voda nebude vytékat.
O6 Co se stane, když uděláme druhý (třetí, ...) otvor A' ve stejné výšce?
(Voda nebude vytékat. PROČ?)
O7 Co se stane, když láhev otevřeme? – obr. 3
(Voda vytéká. PROČ?)
O8 Změní se rychlost vytékané vody když láhev stlačíme?
(Ne. PROČ?)
P4 Úloha na výpočet rychlosti vytékající vody a délky dostřiku
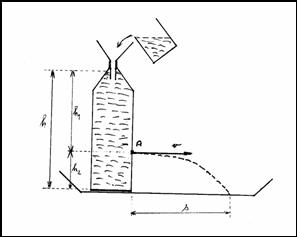
Obr.4
Otvor A uděláme v 1/3 výšky láhve a zajistíme udržování volné hladiny ve stálé výšce h - obr. 4.
V našem případě h = 30 cm, h1 = 20 cm, h2 = 10 cm
Provedeme požadované výpočty a výsledky porovnáme s naměřenými hodnotami.
Řešení:
• Vytékající voda koná vrh vodorovný, tj. ve směru vodorovném pohyb rovnoměrný a pro délku vrhu platí: s = v.t
• Ve směru svislém padá voda volným pádem:
![]()
• Pro rychlost vytékající kapaliny platí ![]() a s = 28 cm.
a s = 28 cm.
(Délku vrhu lze snadno vypočítat i ze vztahu ![]() .)
.)
• Vypočtená hodnota délky vrhu vytékající vodys = 28 cm.
Naměřená hodnotas = 28 cm.
P5 Analogie vrhu vodorovného s vrhem šikmým
Pro délku šikmého vrhu platí vztah
![]() ,
,
tzn., že pro elevační úhel 45° je délka vrhu největší. Můžeme vypočítat a potom (např. podle obr. 2) změřit, že analogicky délka výtoku kapaliny z otvoru v poloviční výšce hladiny je největší.
2 Vazba na matematiku
Pokusy můžeme využít k procvičení dovedností z matematiky např. v následujících dvou případech:
a) Využití Euklidovy věty
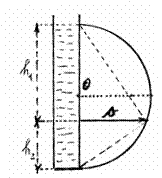

Obr. 5
Z výrazu pro délku vrhu ve tvaru ![]() vyplývá, že délka vrhu bude maximální tenkrát, když
vyplývá, že délka vrhu bude maximální tenkrát, když ![]() bude maximální. Z obr.5 lze Euklidovu větu napsat ve tvaru
bude maximální. Z obr.5 lze Euklidovu větu napsat ve tvaru ![]() , tzn. že délka vrhu bude mít největší velikost pro h1 = h2 = h/2.
, tzn. že délka vrhu bude mít největší velikost pro h1 = h2 = h/2.
b) Určení průměru válce
Dáme žákům úkol vypočítat průměr otvoru vytékající kapaliny a výsledek porovnat s hodnotou naměřenou (např. tak, že kontaktním měřidlem změří průměr jehly, kterou jsme otvor v PET láhvi udělali). Poradíme jim, aby změřili objem vody, která vyteče za dobu τ kruhovým průřezem S nádoby, tj. objem válce V = Svτ.
To, že hodnoty budou odlišné, může být zajímavým tématem diskuze nad rámec vzdělávacího programu.
3 Stabilita těles
Stabilitu těles určuje práce, potřebná k otočení (přemístění) tělesa ze stálé rovnovážné polohy do polohy vratké. Pro otáčení tělesa není rozhodující síla, ale moment síly. Zkušenosti ukazují, že tento pojem je pro žáky značně obtížný.
K dobrému pochopení obou pojmů přispívá i řešení konkrétní úlohy na určení stability kvádru. To znamená umět vypočítat:
a) práci W, kterou musíme vykonat abychom kvádr překlopili,
b) sílyFA, FB, FK, FT, FL, kterými musíme působit kolmo na rameno síly v příslušných bodech, když osu otáčení tvoří hrana lišty Z – viz obr. 6.
Výpočet ukáže a pokus potvrdí, který způsob překlopení je nejvhodnější. Potřebné údaje (hmotnost tělesa a jeho rozměry) žáci změří, provedou výpočty a výsledky porovnají s hodnotami naměřenými.
Nutné pomůcky: délkové měřidlo, siloměr, pravoúhlý trojúhelník, motouz, nůžky, jehlici (pro „znázornění“ těžiště), olovnici.


Obr.6 (vlevo) Obr. 7 (vpravo)
Při řešení jsme použili krabici o rozměrech (29,0 × 27,6 × 10,0) cm3, která měla hmotnost 0,450 kg, místo olovnice jsme použili golfový míček na vlákně, který jsme pověsili na jehlici procházející těžištěm – (obr. 7). Vypočtené výsledky byly v dobré shodě s naměřenými hodnotami: W = 0,68 J; FA = 2,25 N; FB = 1,56 N; FK = FT = FL = 3,10 N.
Jsem přesvědčen o tom, že vědomosti a dovednosti získané takovým způsobem si žáci snadněji a trvaleji zapamatuj.
Literatura
1. JANÁS, J., TRNA, J. Konkrétní didaktika fyziky I. Brno: MU, 1995.
2. BEDNAŘÍK. M., ŠIROKÁ, M. Fyzika pro gymnázia. Mechanika. Praha: Prometheus, 2000. ISBN 80-7196-176-0