O příspěvku
PDF ke staženíNáhoda v chování fyzikálních objektů
Abstrakt
V elektronovém mikroskopu lze vytvořit dvě elektronové vlny, při jejichž překrytí dochází k interferenci. Při krátké expoziční době můžeme velmi dobře pozorovat dopady jednotlivých elektronů na film, tedy částicový charakter elektronů. Při dlouhé expoziční době je na filmu patrný interferenční obrazec, který prokazuje vlnový charakter jednotlivých elektronů.
Dopady jednotlivých elektronů jsou náhodné, při pozorování velkého množství elektronů se však projeví zákonitosti. Elektrony se shlukují v místech s vyšší pravděpodobností dopadu.
Analogicky, zhotovený mechanický model kuliček padajících mezi rozptylovými centry studentům názorně demonstruje funkci náhody ve fyzice a matematické zpracování je zase ukázkou využití počtu pravděpodobnosti.
Spory o podstatu světla
V 17. století se začaly formovat dvě základní teorie na podstatu světla – teorie částicová (korpuskulární) a teorie vlnová (undulační), které spolu soupeřily. Zastáncem teorie částicové byl Isaac Newton, který svojí obrovskou vědeckou autoritou zastínil vlnovou teorii Christiana Huyghense. Je třeba však říci, že obě teorie uspokojivě vysvětlovaly odraz a lom světla.
S objevy nových vlastností světla (ohyb, interference, polarizace) pozvolna začala vítězit vlnová teorie. V 19. století ji rozvinuli Young a Fresnel, kteří vysvětlovali pozorované jevy jako vlnění éteru. V témže století však Maxwell teoreticky odvodil, že světlo není vlnění éteru, ale jde o vlnění elektromagnetické. Jeho teorie vysvětlovala všechny známé vlastnosti světla a zdála se být dokonalá.
Pak byl ale objeven vnější fotoelektrický jev a Comptonův jev, které vlnová teorie vysvětlit nedokázala. Řešení problémů vymyslel Einstein ve století dvacátém. V slavném roce 1905 (letos slavíme sté výročí) uveřejnil svoji rovnici fotoelektrického jevu hf = Wv + Ek, kde člen hf představuje energii dopadajícího světelného kvanta, Wv je výstupní práce elektronů a Ek je kinetická energie fotoelektronu. Teorie světelných kvant (fotonů) vysvětlila fotoelektrický i Comptonův jev natolik úspěšně, že byla vědeckou veřejností přijata a Einstein obdržel Nobelovu cenu. Fyzikové museli připustit dualismus světla – světlo se chová jako vlnění i jako proud částic.
Vlnové vlastnosti částic
V roce 1924 uveřejnil teoretický fyzik Louis de Broglie následující hypotézu: Když se světlo chová jako vlnění i jako proud částic, proč by se částice (elektrony, neutrony, atomy…) nemohly chovat jako vlny?
Zároveň navrhl, že vlnová délka přiřazená částici by mohla být dána vzorcem: ![]() , kde p je hybnost částice.
, kde p je hybnost částice.
Čekalo se 3 roky, než experimentátoři Davisson a Germer při studiu elektronů rozptýlených po dopadu na monokrystal niklu objevili jejich interferenci. Navíc potvrdili de Brogliův vztah pro vlnovou délku. Příroda ukázala svoji symetrii ve světě elementárních částic.
Elektronový mikroskop
Ke studiu malých objektů byl vyvinut optický mikroskop, který sehrál obrovskou roli nejen ve fyzice, ale i v materiálovém výzkumu, biologii, medicíně… Jeho rozlišovací schopnost v řádu mikrometrů je však omezena vlnovou délkou viditelného světla.
Pro studium objektů na úrovni atomárních rozměrů bylo třeba použít vlnění o kratších vlnových délkách. Zde se právě nabídl svazek elektronů, u nichž lze vlnovou délku nastavit urychlujícím napětím. Vznikl elektronový mikroskop, s rozlišením řádově 0,1 nm
Popišme si špičkový elektronový mikroskop Philips CM200, který používá Technická universita v Drážďanech. Bude nás zajímat, jak mikroskop demonstruje vlnový a zároveň i částicový charakter elektronů.
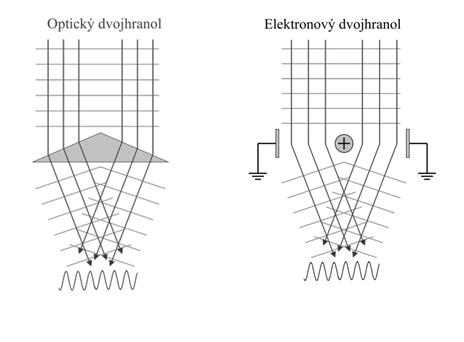
Levý obrázek znázorňuje, jak vznikne interference světla po průchodu např. skleněným hranolem. Pravý obrázek je analogie pro svazek elektronů. Elektrony procházejí kondenzátorem, v němž je nataženo vodivé kladně nabité vlákno. Paprsky jsou zakřiveny elektrickým polem (vynálezci elektronového dvojhranolu jsou G. Möllenstedt a H. Düker [1]).
V obou případech můžeme na filmu nebo CCD kamerou registrovat soustavu interferenčních proužků. Vzhled je ovlivňován napětím na vlákně.

pozn.: Stupnice vlevo udává napětí na vlákně
V elektronovém dělu jsou elektrony extrahovány napětím 3 kV až 4 kV z wolframové špice o průměru 0,5 mm. ve vakuu řádově 10-6 Pa. Urychlující napětí je běžně 100 kV až 300 kV.
Kondensor a objektiv se sestávají z elektromagnetických čoček a upravují elektronový svazek. Vakuum v kondensoru je řádově 10-5 Pa.

Philips CM200
Vakuum v pozorovací komoře má hodnotu 7.10-5 Pa, obraz se snímá CCD kamerou.
Vodivé vlákno v elektronovém dvojhranolu se vyrábí tažením skelného vlákna o průměru 0,5 mm v kyslíko-vodíkovém plameni. Na sklo se napaří 50 nm silná vrstva zlata.
Celý mikroskop váží přes 1 tunu.
Na fotografii pořízené v jiném elektronovém mikroskopu university v Tübingenu sledujeme chování dopadajících elektronů [2].

Po 0,02 s je rozložení zcela chaotické. Ani po 10 s není příliš zřejmá zákonitost v dopadu elektronů. Po 120 s se však již jasně rýsují místa s maximální pravděpodobností dopadu a mezi nimi minima.
Z fotografie jsou patrné dvě důležité skutečnosti: vlnově částicový charakter elektronů a náhodnost v kvantové mechanice.
Částicový charakter je zřejmý z toho, že každý elektron – jedna částice – dopadnuvší na film, vytvoří světlý bod. Vlnový charakter je zřejmý z toho, že se elektrony shlukují do interferenčních proužků, což je typické pro skládání vln. Hustota toku elektronů v mikroskopu (tedy elektrický proud emitovaný z elektronového děla) je zvolena tak, že v každém okamžiku se v mikroskopu nachází pouze jeden elektron. To znamená, že každý jednotlivý elektron má zároveň částicový i vlnový charakter.
Náhoda se projevuje následujícím způsobem. O jednotlivém elektronu se nedá dopředu prohlásit, kam dopadne. Napohled vzniká chaos. Pokud však použijeme velký soubor elektronů, najdeme pravidelnost – místa se známou, teoreticky předpověditelnou pravděpodobností dopadu elektronu – interferenční proužky.
Názornou ukázku tohoto procesu umožňuje bezplatný program Dualismus.exe , který byl vytvořen pro tento referát.

Galtonova deska — teorie
Je vidět, že k popisu chování elektronů je třeba používat pravděpodobnost. Matematika zná pojem Galtonova deska.
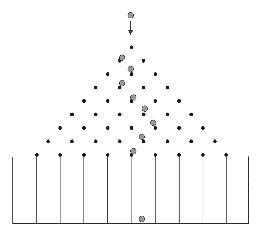
Jde o panel, ve kterém padající kulička naráží do překážek (rozptylových center) uspořádaných do tvaru trojúhelníku a nakonec zapadne do některé z přihrádek. Dopad jedné vybrané kuličky je nepředvídatelný. Pokud však vhodíme velké množství kuliček, dojdeme k určitému zákonitému rozdělení.
Předpokládejme, že na každém rozptylovém centru je pravděpodobnost 1/2 odrazu kuličky vlevo a 1/2 pravděpodobnost odrazu kuličky vpravo. Kulička by měla narážet v každé řadě. Kolik „cest“ vede Galtonovou deskou?
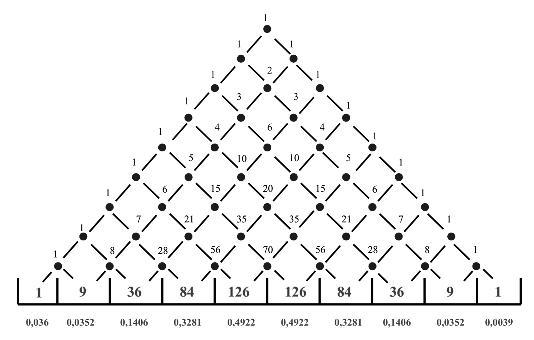
Přiřadíme každému rozptylovému centru hodnotu, která značí počet cest vedoucích do tohoto centra. Kulička padá na vrchol po jediné cestě, přiřadíme tedy vrcholu hodnotu 1. Ve druhé řadě jsou dva body a každý bude mít také hodnotu 1. Ve třetí řadě mají oba krajní body hodnotu 1. Do prostředního bodu třetí řady se dá dostat z dvou bodů druhé řady dvěma cestami. Sečteme tedy jejich hodnoty a získáme číslo 2. Do libovolného bodu vede tolik cest, kolik získáme sečtením cest dvou bodů, které jsou v řadě nad ním. Tento princip lze opakovat do nekonečna. To je ale známá vlastnost kombinačních čísel, takto se vytváří Pascalův trojúhelník.
V 10 přihrádkách jsou zapsána čísla, která vyjadřují počet cest, jež do nich vedou. Všech cest je zde 512 a z těchto údajů lze vypočítat pravděpodobnost zasažení přihrádky. Vzniká binomické rozdělení n přihrádek, které pro ![]() přejde na Gaussovu křivku.
přejde na Gaussovu křivku.
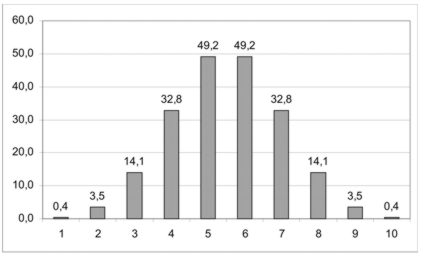
Binomické rozdělení pro 200 kuliček a 9 rozptylových řad
Galtonova deska — provedení

Dřevěná deska má rozměry 480 mm x 1060 mm. Rozptylová centra jsou tvořena 45 vruty o průměru 4 mm a délce 40 mm, na každém vrutu je navlečena bužírka. Vzdálenosti vrutů byly určeny experimentálně a jsou uvedeny na obrázku.
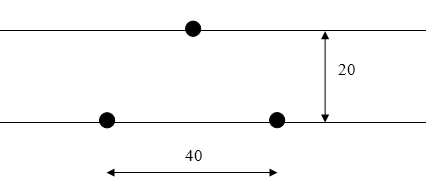
Přihrádky jsou vyrobeny z elektrikářské lišty o šířce 21 mm. Kuličky jsou skleněné o průměru 16 mm, je jich 200. Vhazují se do měděného oka o průměru 20 mm, které je ve výšce 26 mm nad nejvyšším vrutem. V dolní části je deska uzpůsobena k vypouštění kuliček do nádoby. Při experimentování je deska poněkud nakloněna.
Na fotografiích vidíme výsledky dvou pokusů, které jistým způsobem odpovídají teorii. Odlišnosti od teorie jsou způsobeny především skutečností, že jen velmi těžko se dá u padající a rotující kuličky dosáhnout, aby při nárazu byla pravděpodobnost odchýlení vlevo i vpravo na všech rozptylových centrech stejná.
Závěr
Mechanický model padajících kuliček studentům názorně přibližuje složité chování elementárních částic. Jako u konkrétní kuličky nelze předpovědět místo dopadu, tak také místo dopadu jednotlivého fotonu či elektronu je nejisté - náhodné. Při použití velkého množství částic však nejsou všechna místa dopadu stejně pravděpodobná. U Galtonovy desky vzniká binomické rozdělení pravděpodobnosti dopadu a v elektronovém mikroskopu zase interferenční proužky.
Autoři referátu vyvinuli bezplatně šiřitelný program pro simulaci zmíněného jevu Dualismus.exe, připravili fotodokumentaci a popis elektronového mikroskopu Philips CM200 a sestrojili mechanický model - Galtonovu desku.
Literatura
[1] G. Möllenstedt, H. Düker: Fresnelscher Interferenzversuch mit einem Biprisma für Elektronenwellen, Zeitschr. für Physik 42 (1955) 41
[2] Fotografii laskavě poskytl Dr. Michael Lehmann z Technické university v Drážďanech
[3] obr. převzat z E. Völkl, L. F. Allard, D. C. Joy (Editors),
Introduction to Electron Holography, Kluwer Academic / Plenum Publishers,
New York, 1999, ISBN 0-306-44920-X, str. 7