O příspěvku

PDF ke stažení

Patč B.

Soubor pokusů volně navazuje na příspěvek Pokusy s kyvadly, uvedený na druhém ročníku Veletrhu nápadů, Plzeň 1997. Slouží k demonstraci některých typů kyvadel a k ověřování závislostí doby kmitu na jejich parametrech a na vlivu prostředí.

Fyzické kyvadlo s naklonitelnou rovinou kmitu

Potřeby: fyzické kyvadlo s naklonitelnou osou otáčení, stopky, stativ (obr. č. 1)

U kyvadla lze měnit plynule náklon roviny kmitu od svislého směru v rozsahu 0° – 90°, čímž se mění vliv gravitace na dobu kmitu. K nastavení náklonu slouží úhloměr připevněný na stativu a ručička spojená s kyvadlem. Z měření doby kmitu při různých náklonech lze vytvořit graf závislosti doby kmitu na náklonu, resp. na vlivu gravitace, a jeho průběh porovnat se vztahem pro výpočet doby kmitu

,

kde je I moment setrvačnosti vzhledem k dané ose otáčení, a vzdálenost těžiště kyvadla od osy otáčení, m hmotnost kyvadla, g velikost tíhového zrychlení a α úhel náklonu roviny kmitu od svislého směru.

Změny náklonu lze při demonstraci provádět i plynule při rozkmitaném kyvadle.

Simulace torzních kmitů dvouvláknovým kyvadlem

Potřeby: dvouvláknové kyvadlo, zátěže 100 g a 200 g na tenkých vláknech, nastavitelná měrka, měřítko 1 m a posuvné měřítko, stopky, stativ (obr. č. 2).

U kyvadla lze měnit délku vláken, vzdálenost vláken podle měrky, moment setrvačnosti posunem závaží po vodorovné tyči kyvadla podle měrky a simulovat změnu gravitace zavěšením zátěže na kyvadlo v jeho svislé ose. Zátěž se s kyvadlem nenatáčí. Dobu kmitu měříme v závislosti na změnách jednotlivých parametrů, vytváříme příslušné grafy a jejich průběh porovnáváme se vztahem pro výpočet doby kmitu

,

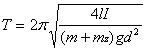kde je l délka vláken, d vzdálenost vláken, m hmotnost kyvadla, m_z hmotnost zátěže, I moment setrvačnosti kyvadla a g velikost tíhového zrychlení.

Poznámka: Nevolíme amplitudy překračující 90°, v opačném případě nemají kmity sinusový průběh.

Kyvadlo nejen pružinové

Potřeby: ocelové pružiny z drátu o průměru 0,35 mm s průměrem vinutí 4 mm s 900 a 500 závity, zátěže 100 g tvaru běžného závaží a 120 g tvaru tyče o průměru 6 mm, milimetrové měřítko, stopky, tenký vlasec, fotografický stativ. Pružiny jsou ke stativu a k zátěži připojeny našroubováním na závit M4.

Amplituda a doba kmitu pružinového kyvadla v průběhu času

Na stativ upevníme kyvadlo s pružinou s 900 závity, zátěží 100 g a rozkmitáme jej s maximální amplitudou (obr. č. 3). Protože taková a takto instalovaná pružina kmitá zřetelně asi 45 minut a vykoná přitom téměř 2000 kmitů, je vhodné současně provádět měření doby kmitu a amplitudy po dvou nebo třech minutách.

Skupině žáků, která bude měření provádět, dejme za úkol, aby stanovila technologii a organizaci měření včetně způsobu záznamu tak, aby bylo možné vytvořit grafy pro změny amplitudy a doby kmitu v průběhu trvání pokusu.

Rozkmitání pružinového kyvadla

Na stativu ponecháme kyvadlo z předchozího pokusu a demonstrujeme možnosti, jak jej rozkmitat. Energii můžeme této soustavě dodat natažením pružiny, vyzdvižením závaží, působením okamžité síly na kyvadlo ve svislé ose, rezonancí silového působení kmitů ruky s vlastními kmity kyvadla v blízkosti závěsu, nebo tak, že závaží podržíme rukou v nulové poloze, druhou rukou uchopíme pružinu v polovině délky a natáhneme její horní část. Po současném uvolnění zátěže i pružiny kyvadlo nekmitá, délkově kmitá jen pružina mezi zátěží a závěsem. Kyvadlo pak rozkmitáme tím, že podržíme krátkodobě pružinu opět v polovině délky. Hodnota takto uvolněné energie pro pružinové kmity závisí na okamžiku stisku pružiny vzhledem k průběhu jejích kmitů, a proto pokus několikrát opakujeme.

Kmity pružinové a torzní

Kyvadlo umístěné na stativu opět ponecháme a k zavěšenému závaží dole připojíme tenký vlasec. Při stažení zátěže vlascem dolů se pružina nejen napne, ale i torzně deformuje tak, že se nepatrně zvýší počet jejích závitů. Touto vlastností je vyvolána souvislost mezi kmity pružinovými a torzními a v případě, že obojí mají stejné frekvence, dochází k přenosu energie mezi oběma typy kyvadel.

Na stativ připevníme pružinu s 500 závity a závažím 120 g (obr. č. 4). Protože torzní tuhost takové pružiny je malá, musí být malý i moment setrvačnosti daného závaží. Rozkmitáme-li kyvadlo jako pružinové, začne kmitat i jako torzní. Amplituda opakovaně narůstá až na hodnotu asi 900° a klesá. Vyvoláme-li v nulové poloze kyvadla kmity torzní, rozkmitává se pružinově s amplitudou asi 8 mm. Torzní kmity jsou patrné na barevné tyčince, připevněné kolmo k tyčovému závaží.

Kyvadlo v nehomogenním silovém poli

Potřeby: matematické kyvadlo s magnetickým a nemagnetickým ocelovým závažím, dva větší ploché feritové magnety a jeden tyčový, vozík pro demonstraci pohyblivého magnetického pole, fotografický stativ.

Zavěsíme kyvadlo s magnetickým závažím a pod něj umístíme libovolně trojici magnetů (viz obr. č. 5). Silové pole bude tak tvořeno třemi poli magnetickými a polem gravitačním; kmity kyvadla budou dále ovlivněny místem závěsu a velikostí i směrem počáteční výchylky. Chování kyvadla je prakticky pokaždé jiné a zdánlivě chaotické. V takovém poli může mít kyvadlo několik stabilních poloh, kolem kterých může kmitat, přičemž kmity mají výrazně nesinusový průběh.

Zátěž kyvadla vyměníme za ocelovou kuličku, snížíme stativ a zkrátíme kyvadlo, aby jeho kmity měly vyšší frekvenci (obr. č. 6). Kyvadlo rozkmitáme a kolmo k rovině kmitů necháme v blízkosti kyvadla rovnoměrným pohybem projet vozík s magnetem. Pozorujeme, jak se stáčí rovina kmitů kyvadla, a porovnáme její počáteční a koncový směr.

Řetízkové kyvadlo

Potřeby: řetízek (nejlépe kuličkový) délky asi 2 m

Řetízek zavěšený nebo držený rukou představuje fyzické kyvadlo s nulovou materiálovou příčnou tuhostí. Tuhost vyvolaná jeho zavěšením je proměnná v jeho délce. Pokud řetízek rozkmitáme jako kyvadlo, kmitá tak, že se během kmitů prohýbá a největší zakřivení má na dolním konci. Z toho vyplývá, že i takto kmitající tuhá tyč, i když to není patrné, je v ohybu namáhána.

Dále kyvadlo rozkmitáme jako kuželové, opět pozorujeme jeho zakřivování a při vyšších frekvencích můžeme vytvořit na kyvadle i další uzly, kromě místa závěsu.

Literatura:

[1] Zahradníček J.: Základní pokusy fysikální. Nákladem vlastním, Brno 1935.

[2] Baník I.: Exotické kmitavé soustavy. In: Sborník konference Veletrh nápadů učitelů fyziky 2. Red.: Rauner K., Randa M. ZČU Plzeň 1997. s. 82-84.