Souhrnný sborník Veletrhu nápadů učitelů fyziky

O příspěvku

PDF ke stažení

Holubová R.

Abstract

A new toy that allows to learn a lot of science. Simple experiments in physics can be done with astrojax. The toy is very simple – three balls on a spring. The fast spinning motion of the balls is based on the physical principles of rotational dynamics.

1 Beyblade

Každý rok kolem vánoc zachvátí naše děti šílenství honby za hračkami, které jsou „in“. Poslední vánoce byly ve znamení hry beyblade – v podstatě se jedná o lepší káču, kterou znali už naše babičky v nejrůznějších provedeních. Na www stránkách zájemci najdou obrázky i popis starších typů těchto rotujících válců, disků, panenek apod. Lze je vyrobit i CD disků, jak jsme už viděli při předešlých prezentacích.

Beyblade má rotační těleso pravidelného tvaru s kovovou osou rotace. Je vybaven speciálními útočnými obručemi a váhovými disky kruhového tvaru, takže tyto součásti mohou rotovat uvnitř vnějšího pouzdra.. Pro uvedení vnitřních částí do rotačního pohybu, vkládáme do beybladu ozubené odjišťovací lanko a prudce za ně zatáhneme.Tím uvedeme gyroskop do pohybu. Doplňky ve váhových discích, rozmístění přídavných závaží, ovlivňuje způsob rotace disku.

2 Astrojax

Hračka, která naše děti tolik nezaujala, ale která je velmi populární v zahraničí, je astrojax. Hračka, která stejně jako beyblade pracuje na fyzikálních principech rotační dynamiky. Astrojax je fyzika pohybu, rozvíjí smysl pro rovnováhu a koordinaci. Jako taková může být použita ve výuce fyziky v mnoha případech.

Astrojax byl vyvinut americkým fyzikem Larry Shawem. Při vývoji astrojaxu si ve fyzikální laboratoři hrál s maticemi, dentálními nitěmi a jejich kombinacemi začal vyvíjet svou hračku. Co se zprvu zdálo jako velmi jednoduché, bylo obtížné popsat matematicky. Úsilí trvalo téměř dva roky a bylo vytvořeno několik set prototypů než se Shaw rozhodl pro jeden model a nechal jej patentovat.

Další překážkou popularizace bylo najít podnik, který by hračku vyráběl - velké společnosti astrojax nepochopily, protože nebyl hračkou spadající do určitých daných kategorií. Shaw proto založil vlastní společnost na jeho výrobu, teprve od roku 2000 se švýcarská společnost ACTIVE PEOPLE ujala produkce a distribuce hračky po celém světě.

Astrojax zvítězil v prestižních soutěžích hraček v USA a má tři záznamy v Guinnesově knize rekordů

3 Co je astrojax?

Na první pohled tvoří astrojax jednoduchá konstrukce – tři vyvážené míčky z pěnového plastu spojené kouskem provázku, přičemž prostřední míček se může po provázku volně pohybovat. Každý míček je přesně vyvážen kovovým závažím umístěným uvnitř plastu. Rychlý kruhový pohyb míčků je založen na fyzikálních principech rotační dynamiky. Vlastnosti astrojaxu byly testovány na orbitální stanici NASA-mission STS-111 v rámci programu NASAs´ TOYS IN SPACE.

4 Základní demonstrace

4.1 Pohyb planet – orbity

Vertikální orbity: tvoříme-li vertikální orbity zjistíme, že provázek se nikdy nepřekříží přes střední míček. To proto, že vnější míček putuje na jeden konec provázku, prostřední míček rotuje v tomto směru velmi rychle. Ve skutečnosti prostřední míček rotuje rychleji, něž dokážeme pozorovat. Tak rychlá rotace je umožněna tím, že uprostřed míčku je závaží, které soustředí hmotnost míčku do blízkosti jeho středu. Stejného principu využívá krasobruslař při piruetě. Vnější míč obíhá kolem vnitřního. Stejně jako v případě Země-Měsíc žádný z míčů není v klidu, oba míčky jsou v pohybu. Prostřední míček klouče po provázku a opisuje svůj malý orbit, dochází ke ztrátě energie.

Horizontální orbit: Oba míčky obíhají po kružnici. Naše dráhy kolem Slunce a Měsíce kolem Země nejsou sice ideálně kruhové, ale elipsy se neliší mnoho od kružnic (Keplerovy zákony). U horizontálního orbitu prostřední míček neklouže po provázku.

Během horizontálních orbitů prostřední míček neklouže po provázku, energie se neztrácí vlivem tření. Proto horizontální orbity vydrží velmi dlouho bez jakéhokoliv pohybu ruky. Naopak při vertikálních orbitech prostřední míček klouže nahoru a dolů po provázku (posloucháme-li pozorně, lze slyšet šustění). Energie se ztrácí vlivem tření – udržení vertikálních orbitů vyžaduje pohyb ruky – dodání energie.

Odstředivá síla: Když se rychlost horizontálních orbitů zvyšuje, provázek připojený ke krajnímu míčku leží stále více horizontálně. Protože je provázek stále více horizontální, může vyvolávat větší sílu směrem dovnitř na krajní míč. To znázorňuje, že dostředivá síla potřebná k vytvoření kruhové dráhy se zvětšuje se zvyšující se obvodovou rychlostí.

4.2 Úloha

Najděte polohu obou míčků během horizontálního orbitu.

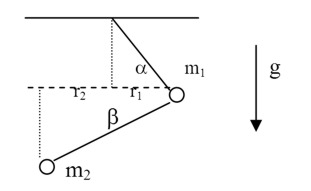
Celková délka lanka je l , m₁ = m₂ = m.

Předpokládáme, že obě hmotnosti se pohybují v horizontálních orbitech o poloměrech r₁, r₂. Kruhová rychlost je obou případech stejná , rovna ω.

Aplikujeme Newtonovskou mechaniku, analyzujeme síly působící na každý míček o hmotnosti m. Každá síla má složku radiální a vertikální. Tím získáme rovnice pro neznámé ω, b, r₁, r₂, T (Tenze = napětí provázku). Rovnice jsou jen 4. Je třeba nalézt další rovnici pro uvedené neznámé – lze využít vztahů pro výpočet délky provázku

Pro hmotnost m₁:

Radiální složka síly

Vertikální složka síly

Pro hmotnost m₂:

Radiální složka síly

Vertikální složka síly

Úpravou rovnic dostaneme

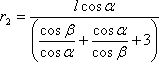
Nyní výsledek dosadíme do rov. (4), abychom mohli vypočítat ω², stále ale neznáme sílu T. Sílu T lze snadno zjistit z rovnice (5), takže dostaneme

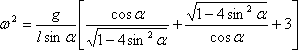
Pro malé úhly α: α → 0 => cos α → 1 a  → 1

Z rovnice (8) dostaneme .

Z rovnice (7) dostaneme .

Dvojité kyvadlo

Po drobné úpravě (ukotvení prostředního míčku) lze demonstrovat pohyb dvojitého kyvadla. Tento pohyb je chaotický, tzn. malá změna vnějšího parametru vede ke zcela novému pohybu. Zatímco řešení jednoduchého kyvadla je bez problému, řešení pohybových rovnic dvojitého kyvadla je složité – je třeba řešit vysoce nelineární rovnice. Použití počítačů umožňuje sledovat na appletech ( které najdeme na www stránkách) pohyb spodního tělesa – opisuje chaotickou křivku. Stejný pohyb koná i spodní kulička astrojaxu. Applety lze najít např. na stránkách http://scienceworld.wolfram.com/physics/DoublePendulum.html

http://www.maths.tcd.ie/~plynch/SwingingSpring/doublependulum.html

Řadu dalších aplikací vám jistě vymyslí vaši žáci.

Literatura

[1] http://www.astrojax.co.uk/science.htm