O příspěvku
PDF ke staženíMěření závislosti indexu lomu kapalin na vlnové délce
Abstrakt
V příspěvku je popsán jednoduchý experiment pro demonstraci a měření závislosti indexu lomu na vlnové délce za pomoci běžných školních pomůcek.
Úvod
Měření indexu lomu kapalin je problém, se kterým se jednou za čas setká každý učitel. Existuje několik způsobů, jak jednoduše měřit index lomu vody i ve školních podmínkách. Například za pomoci akvária tvaru hranolu, nebo dutého zrcadla. Všechna tato měření jsou z hlediska didaktiky přínosná, ale pro přesné měření příliš vhodná nejsou. Naproti tomu profesionální měření jsou sice přesná, ale technicky a mnohdy i fyzikálně náročná. Experiment představený v tomto článku je kompromisem vhodným na půdu škol jako snadný, ale na školní poměry přesný způsob měření indexu lomu kapalin. Navíc je možné měření provádět pro konkrétní vlnové délky a stanovit tak disperzní relaci.
Popis experimentu
Pro sestavení základní verze experimentu není potřeba vyrábět žádné speciální pomůcky. Zde je jejich seznam:
1. pravoúhlé akvárium
2. skleněný hranol
3. stínítko (bílá stěna)
4. zdroj bílého světla se štěrbinou
5. spojná čočka vhodné ohniskové délky
6. délková měřidla (pro měření vzdáleností od milimetrů po metry)
Pravoúhlé akvárium je běžnou součástí školní výbavy. Jeho případné pořízení není příliš nákladné. Skleněný hranol by měl být také běžnou součástí výbavy kabinetu fyziky. Při výběru stínítka je potřeba pamatovat na jeho šířku. Velikost výsledného obrazu je závislá na konkrétním uspořádání experimentu. Může dosahovat i několik metrů, proto je promítání na bílou stěnu asi nejlepším řešením. Světelné zdroje, které se běžně vyskytují na školách, mají pro tuto úlohu značnou nevýhodu. Většina z nich totiž pro výrobu úzkého svazku potřebuje štěrbinu. Tím ovšem dojde k značnému snížení světelného toku a je potřeba zatemnění místnosti. Je možné se tomuto problému vyhnout použitím lineární žárovky. Pro tento experiment jsem si sestavil lineární zdroj bílého světla ze stavařské lampy. Tento zdroj byl inspirován nápadem doc. Zdeňka Bochníčka (viz. [1]). Pořizovací cena se v závislosti na prodejci pohybuje kolem 70-150 korun. Na lampě je pak potřeba provést drobné změny:
1. odstranit odrazovou plochu
2. vnitřní část lampy vystříkat matným černým lakem pro vysoké teploty
3. vybavit lampu odvětráváním (volitelné)
Odstranění odrazové plochy a lakování načerno je nutné pro zvýraznění vlákna žárovky ve výsledném obrazu na stínítku. Tímto však dojde k tomu, že lampa absorbuje více záření, při delším používání se bude přehřívat a může se vysokou teplotou i poškodit. Řešením je odvětrávání, nebo používání lampy jen na kratší dobu. Na obrázku níže vpravo je vidět zdroj světla s odvětrávací šachtou a ventilátorem (6 V, 3 W) a vlevo elektronika pro transformaci a usměrnění síťového napětí. Podle výkonu ventilátoru lze koupit měnič za cenu 100-600 korun. Na většinu lamp je pak možné přišroubovat stojánek tak, aby bylo možné lampu použít na optické lavici. Použití takovéhoto zdroje bílého světla zaručuje, že experiment bude viditelný i za denního světla.


Sestavení experimentu
Zdroj světla umístíme na optickou lavici tak, aby světlo dopadalo kolmo na přední stěnu akvária. Díky tomu, že stěna akvária částečně odráží světlo zpět, je toto nastavení snadné a rychlé. K protější stěně akvária umístíme hranol. Výškově zdroj umístíme tak, aby část světla prošla beze změny směru nad hranolem a zbytek světla se na hranolu lámal. Nyní nalijeme do akvária vodu tak, aby zaplavila část hranolu. Spojnou čočku umístíme na optickou lavici mezi akvárium a zdroj světla, pro zaostření obrazů.
Na stěně (stínítku) za akváriem budou po zapnutí zdroje viditelné tři stopy.
1. Paprsky, které prošly beze změny směru akváriem, vytvoří obraz části štěrbiny (při použití lineární žárovky pak část vlákna žárovky)
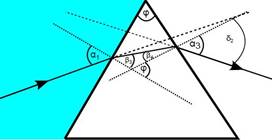
2. Paprsky, které prošly akváriem nad vodou a lámou se na hranolu, utvoří spektrum (na obrázku vlevo)
3. Paprsky, které prošly akváriem ve vodě a lámou se na hranolu, taktéž utvoří spektrum (na obrázku uprostřed)

Odvození rovnice pro výpočty
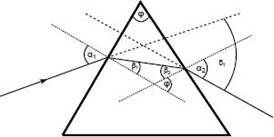
Pro odvození rovnic je nutné si nejprve udělat geometrickou představu problému. Budeme uvažovat situaci, kdy se hranol nachází ve vzduchu a z části ve vodě.
|
Z obrázku zřejmě platí: \[ \delta_1 = \alpha_1 + \alpha_2 - \varphi \] \[ \varphi = \beta_1 + \beta_2 \]Ze Snellova zákona pak: \[ \sin \alpha_1 = n_h \sin \beta_1 \] \[ \sin \alpha_2 = n_h \sin \beta_2 \]kde nh je index lomu skla hranolu. |
Z obrázku zřejmě platí: \[ \delta_2 = \alpha_1 + \alpha_3 - \varphi \] \[ \varphi = \beta_3 + \beta_4 \]Ze Snellova zákona pak: \[ n \sin \alpha_1 = n_h \sin \beta_3 \] \[ \sin \alpha_3 = n_h \sin \beta_4 \]kde nh je index lomu skla hranolu a n je index lomu kapaliny (vody). |
Kombinací předešlých rovnic pro situaci ve vzduchu a jejich úpravou lze získat index lomu skla hranolu jako funkci úhlu dopadu, lámavého úhlu hranolu a deviace paprsku po průchodu hranolem, čili \( n_h = f(\alpha_1, \varphi, \delta_1) \). Stejnou cestou pak získáme index lomu kapaliny \( n = f(\alpha_1, \varphi, \delta_2, n_h) \). Dosazením lze získat index lomu kapaliny. Jelikož je odvození (viz. [2]) příliš časově a prostorově náročné, uvádím pouze výsledný vztah:
\[ n = \frac{- \cos \varphi \sin(\delta_2 - \alpha_1 + \varphi)}{\sin \alpha_1} + \] \[ + \frac{\sqrt{ \sin^2 \varphi \sin (\delta_2 + \varphi) \sin(2\alpha_1-\delta_2 - \varphi) +[-\sin (\alpha_1-\varphi - \delta_1) + \sin \alpha_1 \cos \varphi]^2 }}{\sin \alpha_1} \]Rovnici lze však značně zjednodušit, umístíme-li hranol k zadní stěně akvária tak, jako je vidět na následujícím obrázku. Za předpokladu, že paprsek dopadá kolmo na stěnu akvária, platí, že se úhel dopadu rovná lámavému úhlu hranolu, tedy \( \alpha_1 = \varphi \).
Vztah pro výpočet indexu lomu má tedy tvar:
\[ n = \frac{- \cos \varphi \sin \delta_2 +\sqrt{ \sin^2 \varphi \sin (\delta_2 + \varphi) \sin(\varphi-\delta_2) +[\sin \delta_1 + \sin \varphi \cos \varphi]^2 }}{\sin \varphi} \]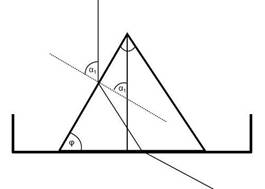
Měření
Při samotném měření, je nutné určit lámavý úhel hranolu. Jednoduše pomocí úhloměru, nebo změřením délek stran hranolu a použitím kosinové věty. Změřený úhel je pak konstantou. Jedinými proměnnými v experimentu zůstávají deviace paprsků po průchodu soustavou. Nejjednodušší způsob jejich určení se zdá být výpočtem z kosinové věty, tedy měření úhlu převést na měření vzdálenosti. Měříme-li měřidlem s chybou 1cm, dostaneme překvapivě dobré výsledky.
Výsledky s použitím zdrojů se známou vlnovou délkou:
| vlnová délka |
n (vypočtené) |
odhad chyby |
n (tabulkové) |
| 670 (červená) |
1,3320 |
0,0022 |
1,3310 |
| 533 (zelená) |
1,3365 |
0,0022 |
1,3352 |
| 476 (modrá) |
1,3383 |
0,0060 |
1,3379 |
Využití
Výhodou experimentu jsou nízké požadavky na znalosti fyziky. Pro úspěšné pochopení je třeba znát pouze Snellův zákon lomu. Z didaktického hlediska je experiment velmi názorný: jestliže zapneme zdroj a až poté vložíme paprskům do cesty hranol, uvidíme, co se s paprsky vlastně děje. Nejprve procházely přímo, a pak jsou hranolem lámány. Po zalití části hranolu vodou pak vidíme, že prostředí, kterým světlo prochází, má zásadní vliv na jeho šíření. Paprsky, které prošly vodou, se totiž lámou jinak než paprsky procházející vzduchem. Velkou výhodou je pak, že všechny tři výsledky jsou současně viditelné na stínítku. Experiment je tak i vhodným kandidátem jako pomůcka při výkladu a demonstraci lomu světla.
Jelikož index lomu vody závisí na koncentraci látek v ní rozpuštěných (např. kuchyňské soli), je možné tuto metodu použít přímo pro měření závislosti indexu lomu na koncentraci rozpuštěné látky.
Další možností je také měření závislosti indexu lomu vody na její teplotě. Tento experiment je však velmi náročný na přesnost měření. Stopa modrého laseru (\(\lambda = 476 \)) se na stínítku vzdáleném od zdroje 11,76 m posunula o 5,2 cm při změně teploty z 36 °C na 56 °C. Stanovení celé závislosti je při použití běžných měřidel takřka nemožné.
Závěr
Prezentovaný experiment je matematicky náročný a nevhodný pro ruční výpočty. Fyzikálně je však velice jednoduchý a názorný.
Literatura
[1] Bochníček Z.: Zobrazení v IR oblasti s využitím termocitlivých fólií. Veletrh nápadů učitelů fyziky 17. Praha 2012.
[2] Učební texty k přednáškám z optiky