O příspěvku
PDF ke staženíBalistika bezpečně
Abstrakt
Mechanika byla a dodnes většinou zůstává úvodní částí středoškolské fyziky. Její přitažlivost pro žáky a studenty postupně klesá, protože mechanické jevy a experimenty nemohou konkurovat atraktivitě optiky nebo elektřiny a magnetismu. Příspěvek nabízí střelbu z „pneumatického děla“ a spojení experimentu, měření a využití jednoduchého programu. Touha vystřelit si je vlastní každému dítěti a z dětství přetrvává alespoň do školských let. Tak proč ji nevyužít ve fyzice.
Konstrukce
Základem je vhodná tlaková nádoba. V tomto případě jde o použitý práškový hasicí přístroj, jehož nádoba má vnitřní objem přibližně 1 litr. Nádoba je zkoušena na tlak 25 barů, a protože v experimentech bude natlakována maximálně na dva bary, nehrozí její poškození. Spouštěcí ventil je odstraněn a na jeho místo vložen ventil určený pro bezdušové pneumatiky. Do dna nádoby je vyvrtán otvor pro připojení elektromagnetického ventilu. Montáž je provedena pomocí topenářských fitinků, běžně dostupných např. v Baumaxu (rozměr 3/8²). Na výstup elektromagnetického ventilu je připojena „hlaveň“, což je PVC trubka (vnější průměr 32mm, tloušťka stěny 1,8mm, délka 1m). Elektromagnetický ventil je jedinou dražší součásti konstrukce. Ventil od firmy GSR, Typ 40TM KO5 10390 byl zakoupen za 1 300 Kč. Ventil otevírá velmi rychle a to je důvod k jeho použití – mechanický kohout není použitelný.
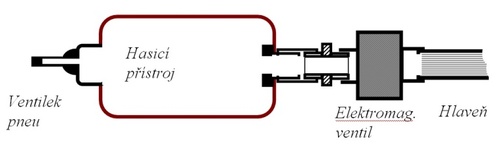
Obr. 1 Náčrt konstrukce pneumatického děla
Střelivo použité pro experiment musí být bezpečné, levné a lehce nahraditelné. Osvědčily se použité korkové zátky. Mají průměr přibližně 2,0cm a jedinou úpravou je zakulacení čelní plochy. To lze provést na hrubém skelném papíru nebo rašplí. Pro výstřel je nutné zátku utěsnit v hlavni – zátka je podkaliberní náboj. Jako ucpávka se hodí kosmetické tampónky. Tampónek přiložený na zadní čelo náboje lehce stočíme kolem zátky a zasuneme do hlavně. Vhodnou tyčkou pak náboj zasuneme na dno hlavně. Příprava k výstřelu končí natlakováním na tlak 2 bary. K napumpování lze použít libovolnou pumpičku nebo malý kompresorek. V každém případě je nutné kontrolovat během huštění tlak. Osvědčená hodnota 2 bary dává dostřel kolem 20m. Střela poměrně brzy zpomalí svůj let a je možné snadno sledovat místo dopadu i tvar trajektorie. Příprava k výstřelu je manuální činnost pro žáka a zaujme i dítě. Odměnou je stisk tlačítka na šňůře k elektromagnetickému ventilu, relativně tichý výstřel a sledování střely.

Obr. 2 Konstruktér a dělostřelec
Na dalším snímku je pohled na celé pneumatické dělo s výjimkou částí hlavně – ta už se do záběru nevešla.

Obr. 3 Pneumatické dělo
Elektromagnetický ventil v detailu a jeho montáž usnadní případnou repliku:

Obr. 4 Detail montáže ventilu
Poslední snímek ukazuje dva typy střel. „Špunt“ neboli korková zátka bez stuhy letí dále, se stuhou je vhodná pro pozorování tvaru trajektorie.

Obr. 5 Střely
Trochu teorie
Středoškolský kurz fyziky dříve obsahoval i vrh šikmý ve vakuu a studenti dokázali odvodit vzorce pro dálku dostřelu i maximální výšku letu střely: Jestliže střela startuje rychlostí \(\vec{v}_0\) a počáteční rychlost svírá s vodorovnou rovinou úhel α, bude stoupat po dobu \( T = \frac{v_0 \sin \alpha}{g}\), dosáhne maximální výšky \(h_{max} = \frac{(v_0 \sin \alpha)^2}{2g}\) a dopadne ve vzdálenosti \(L=\frac{v_0^2}{g} \sin 2\alpha \).
Střely se obvykle pohybují ve vzduchu a jejich obtékání je turbulentní. Je možné použít pro odpor prostředí Newtonův vzorec ve tvaru \[\tag{1} F_0 = \frac{1}{2}C_xS\rho v^2\] a poté použít zákon síly \[\tag{2} \vec{a}=\frac{1}{m}(\vec{F}_g + \vec{F}_0) .\]
Tíhová síla míří vždy svisle dolů, ale odpor prostředí svůj směr stále mění – míří vždy proti okamžité rychlosti střely. Analytické řešení pohybu střely po balistické křivce neexistuje, ale numerický výpočet se skládá z několika jednoduchých kroků. Jestliže v čase t známe vx, vy, x a y, známe také úhel α, protože platí \[\tag{3} \mathrm{tg}\,\alpha = \frac{v_y}{v_x} .\]
Z rovnice [1] vypočteme velikost odporové síly a pak lze rozepsat vektorovou rovnici [2] do složek, vypočítat okamžité zrychlení ax(t) a ay(t). V čase (t + dt) platí \[\tag{4} v_x(t+\mathrm{d}t) = v_x(t) + a_x\mathrm{d}t, \\ v_y(t+\mathrm{d}t) = v_y(t) + a_y\mathrm{d}t.\] Nová poloha střely má souřadnice \[\tag{5} x(t+\mathrm{d}t) = x(t) + v_x\mathrm{d}t, \\ y(t+\mathrm{d}t) = y(t) + v_y\mathrm{d}t.\]
Zbývá určit nový úhel letu a novou velikost odporu prostředí a opakovat výpočty. Numerické řešení je relativně snadné a k dispozici je program v Pascalu nebo v Delphi. V každém případě musíme znát počáteční rychlost střely, i když v experimentu jde pouze o korkovou zátku.
Výpočet počáteční rychlosti
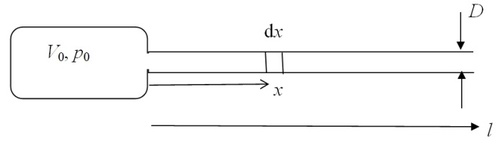
Rozpínání vzduchu je adiabatické, platí \[\tag{6} p_0 V_0^{\kappa} = p V^{\kappa}.\]
Objem plynu se zvětšuje s posuvem střely a ucpávky: \[\tag{7} V= V_0 + Sx.\] Diferenciál práce sil, působících na střelu a ucpávku \[\tag{8} \mathrm{d}W (p-p_a) S \mathrm{d}x,\] kde pa je atmosférický tlak. Integrací pro délku hlavně l dostaneme \[ \tag{9} W = p_0 V_0^{\kappa}\frac{1}{1-\kappa}\left[ \left( V_0 + S l \right)^{1-\kappa} - V_0^{1-\kappa} \right] - S l p_a. \]
Toto řešení předpokládá, že před střelou zůstává atmosférický tlak a zanedbává také tření v hlavni.
Pro výchozí hodnoty l = 0,98 m, D = 28 mm, V0 = 0,001 m3, tlak uvnitř p0 = 3·105 Pa, atmosférický tlak pa = 1·105 Pa, κ = 1,4 dostaneme W = 70,6 J.
Počáteční rychlost získáme ze zákona zachování energie a je třeba znát hmotnost zátky mz = 4g , hmotnost ucpávky mu =0,45g a hmotnost vzduchu v hlavni před střelou v počáteční poloze mv = 0,741 g.
Výpočet dává hodnotu v0 = 165 m·s–1
Výsledky numerického řešení v programu Strela.exe
Pro zadané hodnoty a úhel výstřelu 45° s výškou ústí 1 m nad zemí by střela měla dopadnout ve vzdálenosti 48 m.
Výsledky experimentu
Pro přetlak 2 bary, tj. tlak v nádobce 3·105 Pa, náměr 45° doletí střela bez stuhy do vzdálenosti 22 m a střela se stuhou do vzdálenosti 18 m. Výsledky jsou opakovatelné s přesností ±1 m.
Model matematicky vyjádřený rovnicemi (1) až (9) není dostatečně přesný. Studenti jistě mohou objevit rozpory
• tření ucpávky v hlavni není zanedbatelné,
• před střelou není zachován atmosférický tlak.
Koeficient Cx v programu Strela.exe je volen pro vypuklou polokouli, střela má tvar válce s kulovou čelní plochou. Za letu střela náhodně mění polohu podélné osy. V tomto okamžiku lze nabídnout laborovaní s parametry vkládanými do programu: změnami průměru střely a počáteční rychlosti lze dosáhnou shody experimentu s výpočtem.
Profesionální balistické výpočty střel počítají nikoliv s konstantním koeficientem Cx, ale s tabelovanou funkcí Cx(v). Podrobné informace lze nalézt např. na webu [1].
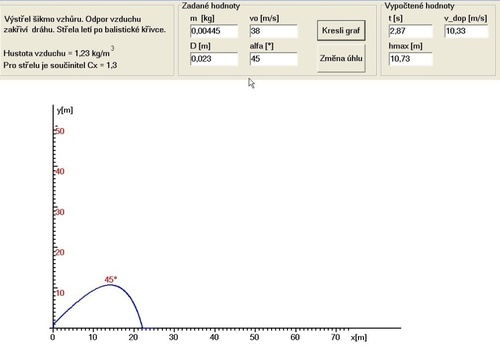
Obr. 6 Výpočet balistické křivky