O příspěvku
PDF ke staženíŠpetka fyziky ve výtahu
V příspěvku je popsáno měření dvou z řady fyzikálních jevů, které lze zaznamenat a alespoň kvalitativně analyzovat při jízdě výtahem; konkrétně jde o přítomnost setrvačných sil v neinerciální vztažné soustavě a změnu tlaku vzduchu s nadmořskou výškou. Použit byl měřicí systém Vernier LabQuest spolu se čtyřmi čidly: barometrem, low-g akcelerometrem, digitálním siloměrem a integrovaným teplotním čidlem. Rozbor získaných dat byl proveden pomocí lineární regrese a statistických funkcí programu Vernier Logger Pro kvůli snazšímu exportování grafických závislostí; bylo by však možné využít jakýkoli jiný nástroj pro zpracování dat, např. tabulkový kalkulátor typu Excel či OpenOffice Calc nebo samotný LabQuest přímo na místě „v terénu“.
Stručný teoretický popis sledovaných jevů aneb co od měření očekávat
Projevy setrvačných sil při jízdě výtahem patří k standardnímu středoškolskému učivu, které lze najít např. v [1] nebo [11]. Pokud má zrychlení výtahu směr vzhůru (rozjíždění cestou nahoru a brzdění cestou dolů), působí těleso na podložku nebo na závěs větší silou než je jeho tíha v klidu, naopak má-li zrychlení výtahu směr dolů (rozjíždění cestou dolů a brzdění cestou nahoru), působí na závěs nebo podložku silou menší. V níže popsaných případech bylo použito závaží o hmotnosti 0,5 kg.
Zkoumání závislosti tlaku vzduchu na nadmořské výšce se stalo námětem k zajímavým školním experimentům řady autorů (viz např. [5], [9], [10]). Uvnitř budov lze teplotu považovat za konstantní a závislost tlaku vzduchu p na nadmořské výšce z při termodynamické teplotě T v tíhovém poli s tíhovým zrychlením g modelovat tzv. barometrickým vzorcem (jeho odvození ze základní rovnice rovnováhy kontinua a stavové rovnice ideálního plynu lze najít v řadě vysokoškolských učebnic, viz např. [4]) \[ p = p_1 \exp \left[ -\frac{gM_m}{RT}(z - z_1) \right], \] kde pro vzduch R/Mm = 289 J∙kg-1∙K-1. Protože v našem případě bude rozdíl výšek (z – z1) malý, vystačíme s lineární aproximací (prvními dvěma členy MacLaurinova rozvoje exponenciální funkce) \[ p \approx p_1 \left[1 -\frac{gM_m}{RT}(z - z_1) \right]. \]
Tento závěr podporuje i vypočtený korelační koeficient lineární regrese, který se ve všech níže uvedených případech pohybuje v rozmezí 0,98 – 0,99. Dodejme, že závislost tlaku na nadmořské výšce jako první předpověděl Blaise Pascal (a experimentálně ověřil jeho švagr Florin Périer výstupem na horu Puy-de-Dôme s rtuťovým barometrem v roce 1648), exponenciální průběh objevil Edmund Halley roku 1686 a vzorec teoreticky odvodil Pierre Simon de Laplace.
Měření
Měření byla provedena ve třech různých typech výtahů, a to v nové budově PřF UP (6 podlaží), v RCO Olomouc (19 podlaží) a v panelovém domě na předměstí Olomouce (9 podlaží). V prvním a třetím případě byl nezávisle změřen výškový rozdíl, pomocí něj a zaznamenané doby jízdy výtahu byla určena průměrná rychlost výtahu.
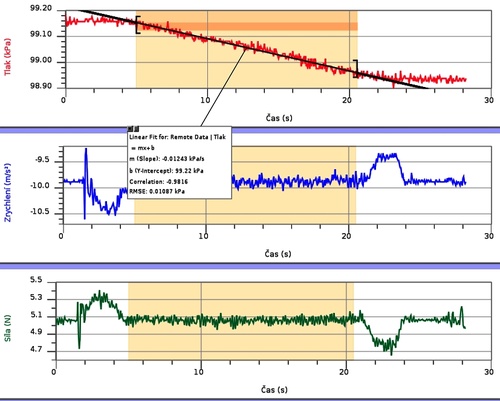
Obr. 1. Záznam měření z nové budovy PřF UP (jízda nahoru, 25 vzorků/1s)
Z grafů je zřejmé působení setrvačné síly při rozjíždění i zastavování výtahu. Méně uspokojivý se ukázal odhad rychlosti výtahu pomocí akcelerometru, neboť měřená zrychlení jsou poměrně malá (např. ve vlaku lze dosáhnout mnohem lepších výsledků, viz [3]), k přijatelným hodnotám rychlosti vedlo použití údajů siloměru vydělených hmotností použitého závaží 0,5 kg a nahrazení setrvačné síly při rozjíždění její průměrnou hodnotou (s výjimkou panelového domu, jehož starší výtah jede pomaleji a relativní chyba v určení rychlosti tímto způsobem byla velká, zde se osvědčilo nezávislé určení překonaného výškového rozdílu).
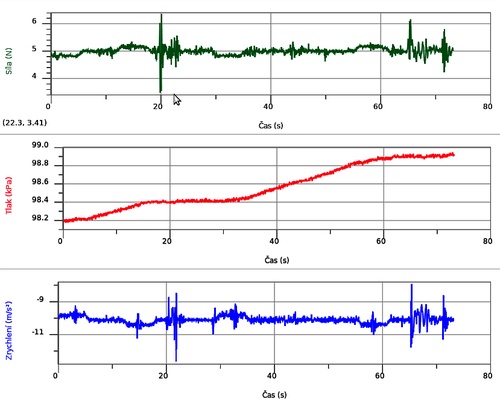
Obr. 2. Záznam měření z RCO v Olomouci (jízda dolů, 25 vzorků/1s); z naměřených dat je vidět, že výtah zastavil a přistoupil další cestující
Pro úsek rovnoměrného pohybu výtahu byl vypočten koeficient lineární regrese Δp/Δt (změna tlaku s časem), jenž byl převeden na koeficient Δp/Δz (změna tlaku s výškou) vystupující v barometrickém vzorci pomocí rychlosti výtahu v (proto jde z hlediska měření o důležitý údaj) podle vztahu \[ \frac{\Delta p}{\Delta z} = \frac{\Delta p}{\Delta t} \cdot \frac{1}{v} \] porovnán s teoretickou hodnotou \[\frac{\Delta p}{\Delta z} = - p_1 \frac{gM_m}{RT}.\]
Za počáteční i konečné hodnoty tlaku byly považovány průměry hodnot před rozjezdem resp. po zastavení výtahu. Získané výsledky a odpovídající teoretické hodnoty jsou shrnuty v následující tabulce (ve všech případech jde o jízdu nahoru):
|
|
Δt (s) |
Δz (m) |
Δp (kPa) |
Δpteor (kPa) |
v (m/s) |
Δp/Δz (kPa/m) |
Δp/Δzteor (kPa/m) |
| PřF UP |
18,1 |
19 |
– 0,23 |
– 0,22 |
1,0 |
– 0,0119 |
– 0,0115 |
| RCO |
45,0 |
67 |
– 0,70 |
– 0,78 |
1,5 |
– 0,0118 |
– 0,0117 |
| panelák |
34,2 |
23 |
– 0,27 |
– 0,27 |
0,7 |
– 0,0126 |
– 0,0116 |
Lanovkou z Pece pod Sněžkou na Růžovou horu
K obdobným měřením se pochopitelně nabízejí i jiné dopravní prostředky než výtah (viz např. [3] a [6]). Změnu tlaku s nadmořskou výškou zaznamenáme i při jízdě lanovkou. V troposféře (tj. zhruba do výšky 11 km nad zemským povrchem) teplota klesá s konstantním teplotním gradientem – 6,5 mK/m (adiabatický model pro vzduch s ϰ = 1,4 dává – 9,7 mK/m [4]), lineární aproximace (první dva členy mocninné řady) závislosti tlaku na nadmořské výšce vychází stejná jako v případě aproximace barometrického vzorce.
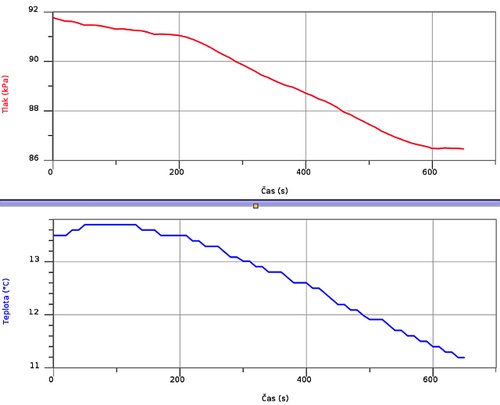
Obr. 3. Pokles tlaku a teploty při jízdě lanovkou
Základní údaje o tomto úseku lanové dráhy zjistíme na internetových stránkách provozovatele http://www.snezkalanovka.cz: Δz = 464 m, uražená vzdálenost 1560 m. Z doby pohybu 650 s vychází rychlost lanovky asi 2,4 m/s a (v přiblížení nakloněné roviny) průměrná rychlost ve svislém směru 0,71 m/s. Koeficient lineární regrese pro pokles teploty s časem přepočítaný pomocí rychlosti ve svislém směru pak dává teplotní gradient –7 mK/m při použití integrovaného teplotního čidla. Naměřená změna tlaku – 5,3 kPa je také v řádovém souladu s teoretickou hodnotou – 5,0 kPa plynoucí z uvažované lineární aproximace. Z průběhu vrstevnic na mapě (popř. přeměřením vzdáleností jejich průsečíků s trasou lanovky) zjistíme, že závislost tlaku na výšce vcelku dobře odpovídá výškovému profilu terénu.
Závěr
Ze získaných výsledků je zřejmé, že touto cestou lze poměrně jednoduše ukázat působení setrvačné síly ve zrychleně se pohybujícím výtahu (i skutečnost, že při rovnoměrném pohybu působí těleso na podložku nebo na závěs stejnou silou, jako když výtah stojí). Pokles tlaku s výškou je pak řádově v souladu s teoretickými hodnotami odpovídající lineární aproximaci exponenciální závislosti dané barometrickým vzorcem.
Poděkování
Tento příspěvek vznikl za podpory projektu "Moderní prostředky ICT v přírodovědných a ekonomických oborech a jejich prezentaci," reg. č. CZ.1.07/2.2.00/07.0062. Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky.

Literatura
[1] Bednařík M., Široká M.: Fyzika pro gymnázia. Mechanika. Praha, Prometheus 2005.
[2] Berberan-Santos M. N., Bodunov E. N., Pogliani L.: On the barometric formula. Am. J. Phys. 65(5), 404 – 412.
[3] Böhm, P.: Fyzika na (školním) výletě aneb akcelerometr ve vlaku. http://fyzweb.cz/clanky/index.php?id=150.
[4] Douglas J. F., Gasiorek J. M., Swaffield J. A.: Fluid mechanics. Longman Scientific & Technical, 1985.
[5] Erhartová V.: Výlet s barometrem. http://fyzweb.cz/materialy/vylet-s-barometrem.
[6] Jermář J.: Fyzika cestou do školy. http://fyzweb.cz/clanky/index.php?id=131.
[7] Ландaу Л. Д., Лифшиц E. M.: Механика сплошных сред. Наука Москва, 1954.
[8] Mikulčák J. a kol.: Matematické, fyzikální a chemické tabulky a vzorce pro střední školy. Praha: Prometheus, 2009.
[9] Pazdera V.: LabQuest – měření „v terénu“. In: Sborník konference Veletrh nápadů učitelů fyziky 13. Ed.: Rauner K., ZUČ Plzeň 2008, s. 147 – 151.
[10] Pazdera V.: LabQuest – měření „v terénu“. Matematika-Fyzika-Informatika 18(9), s. 543 – 547.
[11] Svoboda E. a kol.: Přehled středoškolské fyziky. Prometheus Praha, 2006.