O příspěvku
PDF ke staženíExperimenty se systémem firmy Vernier
Experiment a jeho vyhodnocení jsou nedílnou součástí výuky fyziky. V případě zkoumání některých fyzikálních dějů a jevů může být problematické experiment vyhodnotit bez použití měřicího přístroje. Jednou z možností, jak reálné experimenty vyhodnocovat, je i použití sond firmy Vernier. V příspěvku jsou popsány některé experimenty, které lze s tímto systémem provádět.
Úvod
Řadu fyzikálních experimentů, které jsou přínosné pro výuku fyziky, je nutné vyhodnotit nejen kvalitativně, ale i kvantitativně. V některých případech se ovšem těžko hledají vhodné přístroje, které by učiteli fyziky dobře posloužily – buď na školách nejsou, nebo jsou didakticky nevhodné. Školní experimentální systém Vernier, který ve svém příspěvku [1] popsali v Brně v roce 2009 Pavel Böhm a Jakub Jermář, tyto požadavky splňuje. Rozhraní Vernier LabQuest je přenosné, lze s ním měřit nejen v učebně fyziky, ale také v terénu, naměřená data lze zpracovat přímo v LabQuestu nebo na počítači a to buď v programu Vernier Logger Lite / Logger Pro, nebo v dostupném tabulkovém editoru.
Popis systému
Základem měřicího systému jsou senzory, kterých je v nabídce více než 50. Některé senzory lze používat samostatně, některé lze přímo připojit k počítači pomocí USB, většinou je však nutno připojovat senzory k nějakému rozhraní. Jednoduchá rozhraní Go!Link nebo LabQuest Mini slouží pouze k propojení senzoru s počítačem. Přenosným rozhraním a současně dataloggerem, tedy „krabičkou schopnou zaznamenávat měřená data v terénu“, je LabQuest. V LabQuestu lze rovněž prohlížet grafy a provádět analýzu dat.
Vhodným doplňkem je i software Logger Pro nebo Logger Lite – lze pomocí něj zobrazovat i vyhodnocovat data v počítači, případně je přes schránku operačního systému přenést do tabulkového editoru a následně provádět sofistikovanější vyhodnocení. Ze souboru tabulkového editoru je pak možné data načíst např. i do aplikace Mathematica [2], kde jsem také některá měření dále zpracovával.
Experimenty
Experimentů, které je možné se Vernierem provádět, je celá řada. Já se v tomto příspěvku zaměřím pouze na popis některých z nich. Další jsou pak popsány na internetových stránkách [3] a [4].
Netlumené kmitání tělesa zavěšeného na pružině
Těleso zavěšené na pružině můžeme zkoumat pomocí dvou sond a můžeme vyšetřovat různé charakteristiky tohoto pohybu. Během měření je nutné zachovat klid a nepohybovat se kolem experimentálního zařízení: čidla jsou velmi citlivá a zobrazené výsledky měření by mohly být těmito vnějšími vlivy ovlivněné.
První experiment provedeme s ultrazvukovým čidlem polohy Go!Motion. Těleso s jasně definovaným spodním okrajem (tj. bez výstupků či jiného členění) zavěsíme na pružinu a pod pružinu s tělesem do vzdálenosti zhruba 15 cm až 20 cm umístíme čidlo. Nastavíme čas měření na 5 s a vzorkovací frekvenci na 50 Hz. Před rozkmitáním tělesa zkontrolujeme, že se nachází přesně nad čidlem polohy. Těleso rozkmitáme ve vertikálním směru a spustíme měření. Po skončení měření získáme přímo v LabQuestu (nebo na monitoru počítače) graf závislosti okamžité výchylky kmitajícího tělesa na čase (obr. 1). Grafem je křivka, kterou lze s velkou přesností považovat za sinusoidu. Během krátkého časového intervalu, po který měření probíhalo, nedosáhla odporová síla vzduchu takové velikosti, aby se tlumení výrazně projevilo v grafu. To mohou ovšem fyzikálně rozebrat i sami žáci.
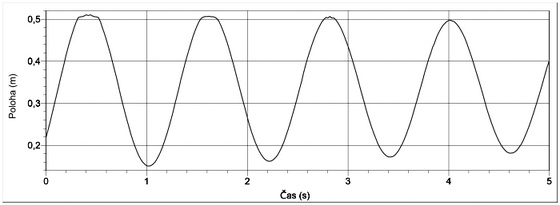
Obr. 1 Graf závislosti okamžité výchylky na čase
Na první pohled graf zobrazený na obr. 1 odpovídá grafům uváděným v učebnicích zabývajících se kmitavým pohybem. Při pozornějším pohledu ovšem zjistíme, že tomu tak není. Rovnovážná poloha nemá nulovou výchylku, ale přibližně 0,3 m (na svislé ose Poloha). To je vzdálenost čidla polohy od závaží v rovnovážné poloze. Zároveň vidíme, že této hodnoty poprvé nedosahuje kmitající těleso v nulovém čase. Proč? A máme první úlohu, nad kterou mohou přemýšlet sami žáci. Graf uvedené závislosti nezačíná v bodě [0; 0,3] proto, že měření začalo v okamžiku, kdy těleso mělo určitou nenulovou počáteční fázi. Tu můžeme z grafu určit pomocí času, ve kterém dosáhlo kmitající těleso poprvé rovnovážné polohy. V ten okamžik je fáze kmitání nulová a na základě frekvence kmitavého pohybu odečtené z grafu můžeme určit počáteční fázi kmitání. Podrobněji je tato úloha komentována v materiálech [4].
Můžeme žáky také vyzvat, aby napsali rovnici závislosti okamžité výchylky na čase, která popisuje tento kmitavý pohyb – to znamená, že je nutné určit amplitudu, periodu a počáteční fázi daného kmitavého pohybu. Při této analýze mohou pomoci analytické nástroje zabudované do programů Vernier. Logger Lite umožňuje zobrazit maximální, minimální a průměrnou hodnotu zobrazeného grafu – tedy hodnoty, na základě nichž lze určit parametry kmitavého pohybu nutné pro napsání výše zmíněné rovnice. Program Logger Pro navíc umožňuje vybraná data proložit jednou z předdefinovaných závislostí (lineární, polynomická, goniometrická, logaritmická,…) případně napsat rovnici vlastní závislosti (viz dále).
Těmito a dalšími úlohami ověříme, zda žáci základnímu kinematickému popisu mechanického kmitání rozumějí.
Současně s grafem závislosti výchylky na čase zobrazí LabQuest i graf závislosti velikosti okamžité rychlosti kmitajícího tělesa na čase. U tohoto grafu je ovšem nutné si uvědomit, že přístroj získává informace o rychlosti numericky, zobrazená funkce tedy nemusí být hladká. Případné odchylky od harmonického průběhu jsou dány právě použitou numerickou metodou výpočtu, volbou vzorkovací frekvence, rušivými vlivy z okolí apod.
Druhý experiment provedeme se siloměrem, na kterém nejdříve nastavíme citlivost podle hmotnosti tělesa, které na pružinu budeme zavěšovat. Parametry měření nastavíme stejně jako v prvním experimentu, rozkmitáme těleso zavěšené na pružině a spustíme měření. Graf závislosti velikosti okamžité síly na čase (obr. 2) je velmi podobný grafu zobrazenému na obr. 1.
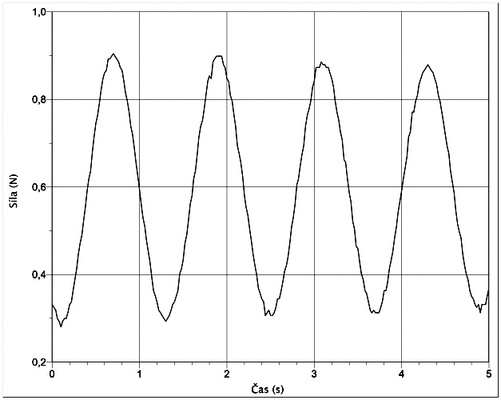
Obr. 2 Graf závislosti velikosti okamžité síly na čase
Nyní můžeme žákům položit následující otázky a dát tyto úkoly: Jaká je hmotnost tělesa, které na pružině kmitalo? Jaká je maximální velikost síly, která na kmitající těleso působila? Jaká je amplituda velikosti proměnné síly působící na kmitající těleso? Jaká je perioda kmitání tělesa zavěšeného na pružině? Napište rovnici pro okamžitou velikost síly působící na těleso v závislosti na čase. Jaká je tuhost použité pružiny? Tuhost pružiny lze přitom určit dvěma způsoby. První z nich vychází ze vztahu pro frekvenci (resp. periodu) vlastních kmitů tělesa zavěšeného na pružině. Tato perioda, kterou lze určit z grafu, závisí na hmotnosti tělesa (tu lze určit pomocí siloměru, na kterém je zavěšeno těleso v klidu) a tuhosti použité pružiny. S využitím matematického vztahu popisující tuto závislost lze tuhost pružiny určit.
Druhá metoda vyplývá z rozboru sil, které na těleso zavěšené na pružině působí v rovnovážné poloze. Svisle dolů působí jeho tíhová síla, která je kompenzována silou pružnosti vyvolanou protaženou pružinou; její velikost je přímo úměrná prodloužení pružiny z její klidové délky a tuhosti pružiny. Obě uvažované síly jsou v rovnovážné poloze tělesa stejně velké. Tíhovou sílu určíme pomocí siloměru, prodloužení pružiny naměříme pravítkem a pak již můžeme určit tuhost použité pružiny. Podrobnější komentář je uveden v materiálech [4].
Odpoví-li na tyto otázky žáci správně, pochopili kinematiku i dynamiku kmitavého pohybu.
Tlumené kmitání tělesa zavěšeného na pružině
Tento experiment je jednoduchou obměnou prvního experimentu. Opět jej můžeme provést s ultrazvukovým čidlem polohy nebo se siloměrem. Rozdílné bude pouze nastavení měření: dobu měření nastavíme na 30 s. Rozkmitáme těleso zavěšené na pružině a spustíme měření. Graf závislosti okamžité výchylky na čase je zobrazen na obr. 3. Na tomto obrázku je zobrazen i teoretický průběh funkce popisující tento kmitavý pohyb (funkce byla vygenerována v programu Logger Pro).
Tuto a jiné fitovací funkce získáme tak, že pomocí myši označíme naměřená data a zvolíme v menu volbu Analýza - Proložit křivku. V tomto případě tlačítkem Define Function otevřeme dialogové okno, do kterého zapíšeme rovnici křivky, kterou chceme naměřená data proložit, tj. rovnici f(x) = A*exp(-E*x)*sin(B*x+C)+D. Potvrdíme tlačítkem OK a pak tlačítkem Try Fit spustíme fitování, během kterého program nalezne hodnoty koeficientů A, B, C, D a E ze zadané rovnice. Výsledná funkce je zobrazena na obr. 3, na kterém je zobrazen i původní graf závislosti okamžité výchylky na čase. Vzhledem k tomu, že nalezená funkce velmi přesně prochází body grafu získanými na základě měření, není naměřená křivka v grafu téměř patrná.
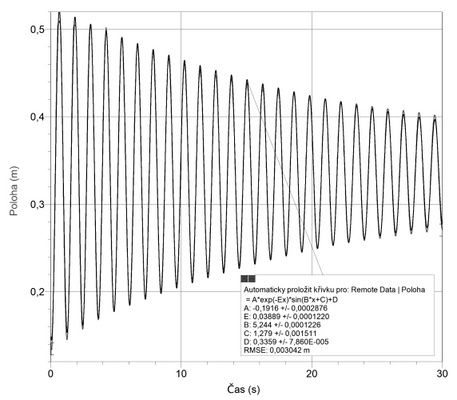
Obr. 3 Graf závislosti okamžité výchylky na čase u tlumeného kmitání
Se žáky můžeme pak diskutovat o tom, proč k získání grafu závislosti okamžité výchylky na čase pro tlumené kmitání stačilo ve srovnání s netlumeným kmitáním pouze prodloužit čas měření.
Tlak vzduchu v balonku
Tlak vzduchu v balonku, ze kterého uniká vzduch, se zcela jistě mění. Zajímavé je zjistit, jak se tento tlak mění v závislosti na čase. To lze zjistit pomocí tlakoměru GPS-BTA. Senzor připojíme k rozhraní (například LabQuestu), nastavíme čas měření na 10 sekund a vzorkovací frekvenci zvolíme např. 5 Hz. Nafoukneme pouťový balonek a opatrně (abychom z něj nevypustili příliš mnoho vzduchu) do něj jeho náustkem zasuneme hadičku od senzoru tlaku. Spustíme měření a současně uvolníme náustek balonku tak, aby vzduch z balonku mohl volně proudit ven. Graf časové závislosti tlaku vzduchu v balonku je zobrazen na obr. 4. Z tohoto grafu je zřejmé, že tlak vzduchu v balonku během jeho vypouštění nejdříve klesá a poté začne růst. Hodnota lokálního minima v závislosti na maximálním tlaku vzduchu v balonku závisí na materiálu balonku.
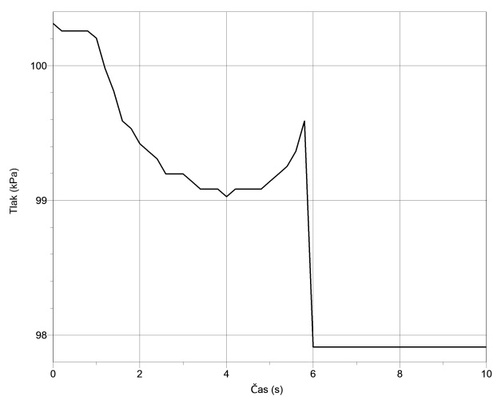
Obr. 4 Graf závislosti tlaku vzduchu v balonku na čase
Tento experiment může sloužit jako motivační experiment ke studiu deformací pevných těles (blány balonku), ale také může sloužit jako srovnávací s analogickým experimentem provedeným s mýdlovou bublinou. V případě mýdlové bubliny je možné pečlivě proměřit závislost tlaku vzduchu uvnitř bubliny na jejím poloměru.
Závěr
Výše uvedené experimenty jsou pouze zlomkem z toho, co vše lze s využitím čidel firmy Vernier zkoumat. Důvod, proč se mi práce s LabQuestem a čidly líbí, spočívá v intuitivním ovládání systému, v jeho mobilitě, intuitivní práci s programem a v možnosti naměřená data zpracovávat v dalších programech. Velkou výhodou z hlediska použití ve škole je snadné ovládání nejen pro učitele, který se LabQuest a jeho příslušenství naučí ovládat během několika minut, ale i pro žáky. Ti jsou ve většině případů na práci s technickými přístroji šikovnější než učitelé, takže ani jim nebude činit ovládání žádné potíže. Navíc z vlastní zkušenosti vím, že je práce s LabQuestem baví. Na druhou stranu není vhodné provádět ve škole experimenty výhradně s touto pomůckou. Žáci by měli mít možnosti vidět a provádět i jiný typ experimentů. Nemluvě o dalších aktivitách během hodin fyziky: řešení typových úloh, hledání souvislostí mezi probíranými fyzikálními jevy apod.
V souvislosti s rozvojem žákových kompetencí je experimentální systém Vernier velmi vhodný z hlediska budování mezipředmětových vztahů ve fyzice, matematice, výpočetní technice, biologii, chemii a dalších disciplínách.
Literatura a zdroje
[1] Böhm P., Jermář J.: Dataloggery ve výuce fyziky aneb Fyzika s Vernierem. In: Sborník konference Veletrh nápadů učitelů fyziky 14. Ed.: Bochníček Z., Navrátil Z. Masarykova univerzita Brno 2009. s. 38-42.
[2] Reichl J.: Využití Mathematicy ve fyzice. In: Sborník konference Veletrh nápadů učitelů fyziky 13. Ed.: Rauner K. Západočeská universita v Plzni, Plzeň 2008. s. 190-194.