O příspěvku
PDF ke staženíKmitavý pohyb trochu jinak
Kmitavý pohyb patří mezi základní fyzikální děje. Většinou se tato část fyziky redukuje na matematický popis děje. Z hlediska motivačního je ale třeba žáky a studenty všech typů škol nejprve seznámit se zajímavými experimenty této oblasti fyziky a až poté provést jejich kvalitativní a kvantitativní analýzu. Na tuto problematiku je nutné také vhodně připravit budoucí učitele fyziky.
Kmitavý pohyb vodního sloupce v U-trubici
Velmi jednoduchý experiment můžeme provést s „U trubicí“, ve které rozkmitáme vodní sloupec. Z hlediska vizualizace je dobré vodu obarvit (např. potravinářskou barvou). Trubice může být skleněná nebo z vhodné průhledné hadice upevněná v stabilních stojanech (držácích). Délka jednoho ramene trubice by měla být cca 1,5 m, aby doba kmitu byla v přijatelných hodnotách (Obr. 1).

Obr. 1
Naplníme-li trubici přibližně do poloviny její výšky vodou a pomalým fouknutím docílíme porušení rovnováhy v U-trubici, dojde po následném otevření konce trubice k rozkmitání vodního sloupce. Tento pohyb se však v důsledku tření kapaliny o stěnu trubice rychle utlumí a v podstatě není možné provést dostatečně přesné měření. Proto je nutné do vody přidat trochu saponátu, abychom snížili tření kapaliny o stěny trubice a docílili menšího útlumu.
Fyzikální rozbor kmitavého pohybu v U-trubici
Snížením hladiny na jedné straně trubice dojde k jejímu stejnému zvýšení na druhé straně trubice, čímž dojde k porušení rovnováhy sil (Obr. 2). Výsledná síla působící na celý objem kapaliny, tj. síla způsobující kmitavý pohyb kapaliny, je určena tíhovou silou kapaliny v trubci mezi horní a dolní hladinou. Tato tíhová síla (Fg) je určena rozdílem výšek hladin v obou trubicích (2y), průřezem trubice, hustotou kapaliny (ρ) a tíhovým zrychlením (g).
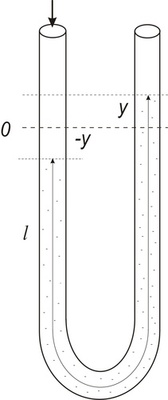
Obr. 2
Velikost této síly můžeme určit vztahem: \(F_g = - \pi \cdot r^2 \cdot 2 \cdot y \cdot \rho \cdot g \).
Znaménko mínus vyjadřuje opačnou orientaci výchylky y a působící síly Fg. Po dosazení do 2. Newtonova zákona a několika jednoduchých úpravách dostaneme diferenciální rovnici 2. řádu s konstantními koeficienty, která představuje rovnici kmitavého pohybu: \[ \frac{d^2 y }{dt^2} + \frac{2\cdot g}{l}\cdot y = 0 .\]
Z řešení této rovnice získáme vztah pro periodu tohoto kmitavého pohybu: \[ T= 2\cdot \pi \cdot \sqrt{\frac{l}{2\cdot g}}.\]
Z výsledného vztahu vyplývá, že perioda tohoto kmitavého pohybu záleží pouze na délce l vodního sloupce. Samozřejmě, že tento vztah platí přesně pouze pro netlumené kmity. Vzhledem k malé hodnotě koeficientu útlumu můžeme ale s přijatelnou mírou přesnosti říci, že v tomto případě je perioda tlumených a netlumených kmitů stejná.
Experimentální ověření
Změření periody je záležitost poměrně jednoduchá, určení amplitudy výchylky je vzhledem k vysoké frekvenci kmitů třeba nacvičit a až poté provést vlastní měření. Nejlépe je v průběhu kmitavého pohybu označit popisovačem na jedné straně trubice všechny amplitudy a až po dokmitání kapaliny změřit jejich velikost, zaznamenat je do vhodné tabulky a sestrojit graf. (Obr. 3)
K ověření platnosti vztahu pro periodu je nutné určit délku vodního sloupce. Tu určíme z objemu kapaliny v trubici a z průměru trubice pomocí vztahu pro objem. Všechny naměřené hodnoty potom zpracujeme do tabulek a vyhodnotíme.
Výpočet periody:
V = 550 ml; d = 19, 5 mm \(\Rightarrow\) l = 1,84 m \(\Rightarrow\) T = 1,9 s
Naměřené hodnoty periody:
10T (s) 19,3 19,3 19,4 19,2 19,4 \(\Rightarrow\) T = 1,9 s
Koeficient útlumu
Z naměřených amplitud určíme koeficient útlumu podle známého vztahu: \[ b = \frac{\ln \frac{A_n}{A_{n+1}}}{T} ,\] pro naše měření vychází: b = 0,161 s-1
Následně můžeme tuto hodnotu dosadit do vztahu pro tlumené kmity: \[ y = A \cdot e^{-bt}\cdot \sin(\omega \cdot t + \varphi) \] a sestrojit graf tlumených kmitů vodního sloupce (Obr. 4).
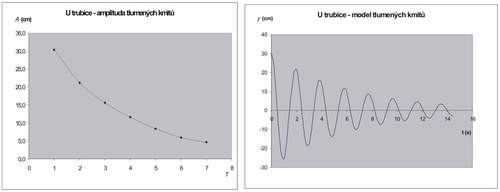
Obr. 3 (vlevo) Obr. 4 (vpravo)
Dále je možné provést porovnání mezi vypočtenou periodou netlumených kmitů vodního sloupce a tlumených kmitů, které charakterizuje vypočtený koeficient útlumu. Pro výpočet periody tlumených kmitů platí vztah: \[ T = \frac{2 \pi}{\sqrt{\frac{4\pi^2}{T_0^2}-b^2}} ,\] kde T0je perioda netlumených kmitů a b koeficient útlumu.
Po dosazení výše uvedených (naměřených a vypočtených) hodnot se potvrdil náš původní předpoklad: \(T = T_0 \dot{=} 1,9\,\mathrm{s}\).
Kmitavý pohyb tyčky na rotujících kotoučích
Další jednoduchý a zajímavý experiment můžeme provést s rotujícími kotouči, na které položíme tyčku. Pokud se kotouče otáčejí „proti sobě“ vlivem různých velikostí třecích sil mezi jednotlivými kotouči a tyčkou dojde k jejímu rozkmitání. (Obr. 5)

Obr. 5
Jak konkrétně sestavit vhodné zařízení? Pro pohon kotoučů je třeba motorek o dostatečném výkonu, který má malé otáčky. Dále je nutné zajistit, aby se oba kotouče pohybovaly stejnou rychlostí a v opačném směru. Toho docílíme např. překřížením poháněcího gumového řemínku mezi oběma kotouči nebo vytvořením ozubeného soukolí s různým počtem koleček. V našem případě jsme zvolili první variantu a jako pohon použili motorek z automobilových stěračů.
Fyzikální rozbor kmitavého pohybu tyčky na rotujících kotoučích
Položíme-li tyčku o délce l a hmotnosti m mírně asymetricky na kotouče, působí na ni tíhová síla Fg, která se rozkládá do dvou normálových sil v bodech dotyku s rotujícími kotoučky. Protože kotoučky rotují opačně, vznikají v bodech dotyku opačně orientované třecí síly F1 a F2. Výsledná síla, která způsobuje pohyb tyčky, je dána rozdílem těchto třecích sil, tj. platí: F = F1g – F2. Je zřejmé, že tato síla má opačný směr než je výchylka y těžiště od osy symetrie (Obr. 6).
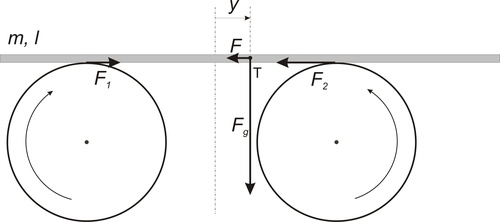
Obr. 6
Vyjdeme-li z označení na obrázku, a ze vztahu pro výpočet třecí síly dostaneme pro celkovou sílu F vztah: \[ F = \left( \frac{m}{2} - \frac{m}{l}\cdot y \right)\cdot g \cdot \mu - \left( \frac{m}{2} + \frac{m}{l}\cdot y \right)\cdot g \cdot \mu,\] \[ F = \frac{-2 \cdot m \cdot g \cdot \mu}{l} \cdot y.\]
Znaménko mínus vyjadřuje opačnou orientaci výchylky y a působící síly F.
Po dosazení do 2. Newtonova zákona a několika jednoduchých úpravách dostaneme diferenciální rovnici 2. řádu s konstantními koeficienty, která představuje rovnici kmitavého pohybu: \[ \frac{d^2 y }{dt^2} + \frac{2\cdot g \cdot \mu}{l}\cdot y = 0 .\]
Z řešení této rovnice vyplývá vztah pro periodu tohoto kmitavého pohybu: \[ T= 2\cdot \pi \cdot \sqrt{\frac{l}{2\cdot g\cdot \mu}},\] kde l = délka tyčky a μ = součinitel tření mezi tyčkou a kotoučem.
Z výsledného vztahu vyplývá, že perioda tohoto kmitavého pohybu závisí pouze na délce tyčky a koeficientu tření. Samozřejmě, že tento vztah platí pouze v případě, kdy koeficient tření m nezávisí na rychlosti pohybu kotoučů a tyčky, kdy tyčka vykonává harmonický kmitavý pohyb.
Paradoxem se zdá být skutečnost, že perioda tyčky nezávisí na její hmotnosti. Můžeme zde naleznout analogii s nezávislostí periody na hmotnosti závaží na kmitající pružině, resp. hmotnosti závaží u matematického kyvadla.
Experimentální ověření
Vzhledem k tomu, že perioda tyčky je poměrně malá (pro délku tyče 0,3–0,9 m cca 1–2 sekundy) je vhodné měřit čas 10 period a potom určit jednu periodu.
Výpočet periody:
l = 0,507 m; m = 0,65 \(\Rightarrow\) T = 1,25 s
Naměřené hodnoty periody:
10T (s) 12,73 12,50 12,46 12,64 12,47 \(\Rightarrow\) T = 1,26 s
Didaktický rozbor uvedených experimentů
S žáky a studenty provedeme fyzikální rozbor uvažovaného jevu. V první řadě musí dojít k poznatku, že se jedná o periodický pohyb. Dále si ujasnit, je-li tento pohyb tlumený či netlumený. Nejdůležitějším úkolem je zjistit, proč k tomuto kmitavému pohybu dochází (porušení rovnováhy sil vychýlením hladin, resp. rozdílné třecí síly na kotoučích).
Dále je vhodné diskutovat o parametrech ovlivňujících velikost periody. Žáci zřejmě budou kromě délky vodního sloupce také uvádět průřez trubice, případně hustotu kapaliny a u rotujících kotoučů potom také hmotnost tyče, resp. počet otáček kotoučů. Na střední škole sdělíme vztah pro periodu bez odvozování a ukážeme jeho analogii se vztahem pro periodu matematického kyvadla.
Z hlediska experimentálních dovedností můžeme procvičit měření periody. Před vlastním měřením provedeme odhad délky periody, který následně ověříme měřením stopkami. Protože doba jedné periody je u obou pokusů poměrně malá, je vhodné změřit např. 10 period a z naměřené hodnoty určit dobu jedné periody.
Aby mohli budoucí učitelé fyziky plnit své poslání, musí být řádně připraveni především po fyzikálně didaktické stránce. Proto při analýze uvedených experimentů provedeme fyzikální rozbor a na jeho základě sestavíme pohybovou rovnici, odvodíme vztah pro periodu kmitu a určíme koeficient útlumu a další závislosti. Získané vztahy potom ověříme experimentálně.
Kromě kvalitativního a kvantitativního řešení úlohy si musí adepti učitelství na této úloze také osvojit didaktické zásady provedení demonstračního experimentu, jeho vyhodnocení pomocí výpočetní techniky a zpracování protokolu. Tyto experimenty lze pojmout jako komplexní úlohu v semináři didaktiky fyziky nebo zadat jako projekt.
Závěr
Cílem tohoto příspěvku bylo ukázat komplexní přístup k dvěma netradičním experimentům na kmitavý pohyb. Fyzikální a didaktická analýza uvedených jevů pak ukazuje jednu z možných variant, jak se této problematiky zhostit.