O příspěvku
PDF ke staženíEasy Java Simulations aneb vlastní applety (poměrně) snadno a rychle
V příspěvku je popsáno volně dostupné prostředí Easy Java Simulations (dále EJS) a na několika konkrétních příkladech jsou ilustrovány možnosti jeho využití k numerickému řešení fyzikálních úloh v rámci seminářů i k doplnění výukových www-stránek. Předváděné simulace budou součástí bakalářské práce, jež by měla být dokončena na jaře roku 2009.
Stručné představení prostředí EJS
Modelování reálných dějů pomocí počítače se stává stále populárnějším doplňkem výkladu v řadě přírodních věd. Uchylujeme se k němu většinou tehdy, když je provedení reálného experimentu z nějakého důvodu nereálné či velmi obtížné. Další významnou oblastí využití je předpovídání a případné optimální ovlivnění přírodních dějů. Konečně z hlediska výuky podobně jako většina pomůcek a nástrojů při uváženém a přiměřeném zapojení do výkladu či při cvičení umožňuje hlubší pochopení zákonitostí a opírá se navíc o přirozený zájem žáků a studentů o výpočetní techniku. Svědčí o tom snahy o využití řady softwarových prostředí k témuž účelu; namátkou zmiňme např. zajímavé programy Famulus, IP Coach nebo GNUOctave (viz [4, 7, 9]).
Klasické programovací jazyky jako např. Fortran, různé varianty jazyka C nebo Java vyžadují odpovídající zvládnutí jejich syntaxe a pomocných nástrojů. Proto – přes veškeré své výhody – jsou pro „běžné“ nasazení ve výuce přece jen dosti náročné. Naštěstí se objevují softwarové prostředky, u nichž se alespoň při základním použití obejdeme bez pokročilé znalosti programování (jež je ale pochopitelně většinou výhodou) a umožňují uživateli soustředit se na samotný matematický model studovaného děje. S jedním z nich bychom chtěli čtenáře seznámit v našem příspěvku.
Balíček EJS vyvinul matematik Francisco Esquembre (University of Murcia, Španělsko) a dal volně k dispozici všem zájemcům pod licencí General Public Licence [3] na webových stránkách [2]. Navázal na projekt Open Source Physics [8], v jehož rámci byla vytvořena (rovněž zdarma dostupná) kompletní členěná sada knihoven, tříd a nástrojů pro programátory k vytváření vlastních fyzikálních modelů v jazyce Java. Bez zkušeností s programováním, je využití prostředků Open Source Physics – alespoň podle našeho názoru – obtížné. EJS je tak prostředníkem, který zpřístupňuje knihovny Open Source Physics i začátečníkům a neprogramátorům. Podle dokumentace programu představuje EJS v podstatě vývojový software využívající OSP knihoven. Umožňuje rychle a jednoduše přepsat matematický model do podoby zpracovatelné počítačem, otestovat jej a vytvořit výslednou Java simulaci popř. www-stránky s výsledným spustitelným appletem.
Také instalace EJS nevyžaduje speciální dovednosti. Instalační ZIP-archiv (o velikosti asi 8,6 MB) lze volně stáhnout z webových stránek [2], nakopírovat (rozbalit) do libovolného adresáře a spustit souborem EjsConsole.jar. Poslední verze 4.0 (z 22. 8. 2008) vyžaduje ke svému běhu Java Runtime Environment (JRE) verze 1.5 a vyšší, jež však většinou uživatelé již nainstalované mají, neboť jinak by nemohli spouštět applety na internetových stránkách. Zájemci o pokročilejší programování v jazyce Java mohou potřebovat Java Development Kit (JDK); obojí nabízí zdarma společnost Sun na stránkách http://java.sun.com/.
K ukládání vytvořených modelů a jejich sdílení mezi uživateli využívá program EJS syntaxi XML (eXtensible Markup Language), s níž se ovšem uživatel díky grafickému rozhraní nemusí zabývat. Primární XML soubory uchovávají všechny potřebné informace pro vystavění simulace, je však třeba je nakopírovat do pracovního adresáře definovaného při prvním spuštění programu. Sdílet lze samozřejmě i exportované spustitelné JAR soubory nebo WWW stránky s applety, avšak s limitovanou možností dalšího ladění výpočetní části modelů. Dodejme, že základní dokumentace je součástí distribuce programu. Z jeho stránek lze také stáhnout řadu hotových simulací a učit se tak na příkladech zkušenějších kolegů. Za pozornost stojí i představení prostředí jeho samotným autorem v časopise Physics Teacher [5].
Jako většina softwarových nástrojů má EJS své výhody i nevýhody, které mohou mít pro každého uživatele různou důležitost. Lze ukázat na omezenou oblast využití (především numerické řešení pohybových rovnic), menší možnost ovlivnění výsledného vzhledu grafického výstupu (např. grafů pro tisk) a do značné míry skrytý vlastní algoritmus numerického výpočtu. Podle našeho názoru však převažují výhody – intuitivní grafické prostředí, přenositelnost mezi různými operačními systémy (Windows, Linux, MAC, Solaris, apod.), dostupnost programu zajištěná licencí GPL a v neposlední řadě možnost exportu na www-stránky, o čemž svědčí řada atraktivních příkladů (viz např. http://faculty.ifmo.ru/butikov/Applets/Gyroscope.html).
Hlavní součásti prostředí
Po spuštění EJS (EjsConsole.jar) se nám otevře EjsConsole (viz obr. 1), ve které můžeme provést základní nastavení, a v druhém okně se pak objeví samotný program. Najdeme zde panel nástrojů, dolní „box“ na zprávy a chybová hlášení a tři hlavní záložky (Description, Model, View), s nimiž pracujeme při vytváření simulace.
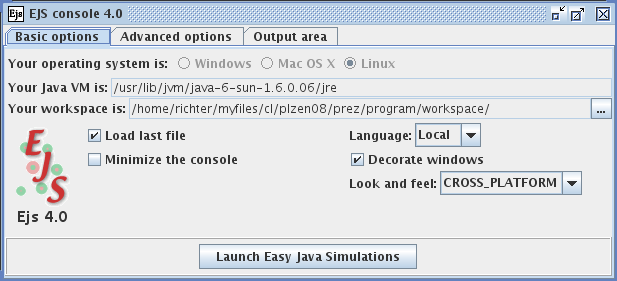
Obr. 1: EJS Console
V panelu nástrojů najdeme ikony pro vyvolání nové, otevření rozpracované a uložení výsledné simulace. Dále se zde nachází důležitá ikona ,,Run‘‘, kterou se všechny simulace spouštějí a zároveň dochází k vytvoření Java appletu. Pro tuto práci využijeme ještě ikonu ,,Edit options‘‘, pod kterou můžeme nastavit několik klíčových vlastností výsledné simulace (včetně formy). Ostatní ikony nejsou pro základní práci nezbytně důležité. V okně pro zprávy a chybová hlášení nám program například napíše, že náš soubor úspěšně uložil a nebo naopak, že nemohl vytvořit výslednou simulaci a zároveň poukáže na obtíže, se kterými se setkal.
Uprostřed dominuje pracovní plocha, do které zadáváme vstupní data, z nichž EJS vytváří konečnou simulaci. Do této oblasti zadáváme jednak stručný popis programu použitý i v exportovaných HTML stránkách (Description), na jiném místě definujeme použité proměnné a zadáváme rovnice, jimiž se má simulace řídit („Model“), a v neposlední řadě vytváříme konečnou grafickou podobu výstupu („View“). Smysl a význam těchto částí lze nejsnáze pochopit na konkrétních modelech.
Příklady
Uveďme čtyři jednoduché příklady využití EJS.
Kmitání závaží na pružině
Z fyzikálního hlediska jde o známý příklad kmitání závaží hmotnosti m na pružině o tuhosti k s tlumením charakterizovaným součinitelem b. Hledáme řešení diferenciální rovnice \[ m\frac{d^2x}{dt^2} = - kx - b \frac{dx}{dt}, \] kde x je výchylka závaží z rovnovážné polohy.
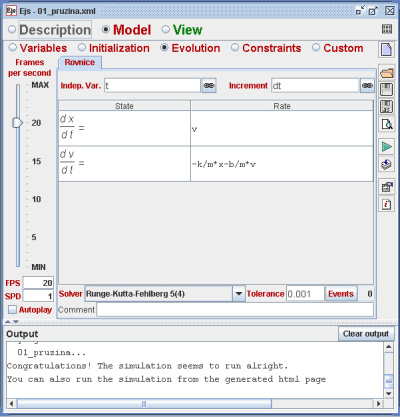
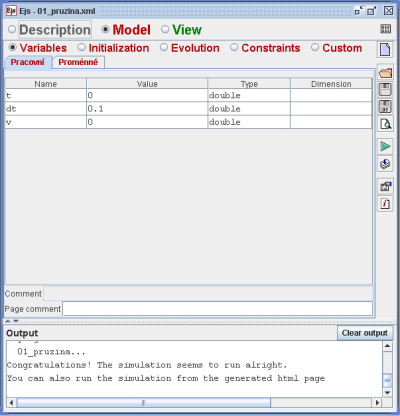
Obr. 2: Zapsání rovnic a proměnných
Tuto diferenciální rovnici druhého řádu můžeme převést na dvě rovnice prvního řádu \[ \frac{dx}{dt} = v, \quad \frac{dv}{dt} = -\frac{kx}{m} - \frac{bv}{m} . \]
V prostředí EJS je pak přepíšeme do části „Model/Evolution“, kde také volíme požadovanou integrační metodu (k dispozici je jich 8 – Eulerova, Rungeova-Kuttova 4. řádu apod.), toleranci, automatické spouštění appletu atd. Musíme také zavést všechny potřebné proměnné v části „Model/Variables“ (viz. obr. 2). K rovnicím připojíme potřebné moduly pro vykreslení křivky („View“) a svážeme je s jednotlivými proměnnými (obr. 3). Poté můžeme vytvořený model uložit a tlačítkem „Run simulation“ spustit. Pokud je vše v pořádku a nenastanou žádné problémy, můžeme sledovat animaci – výstup může vypadat např. jako na obr. 4 (případ zahrnuje i opětovné jednorázové buzení „potažením myší“ při běhu animace). Vidíme, že vstupní hodnoty lze zadávat buď pomocí zapsání hodnot, nebo využít grafických možností (posuvníku).
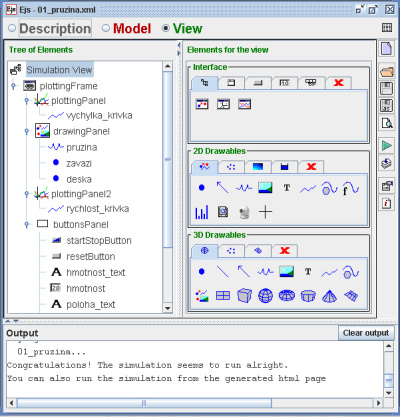
Obr. 3: Definice vzhledu
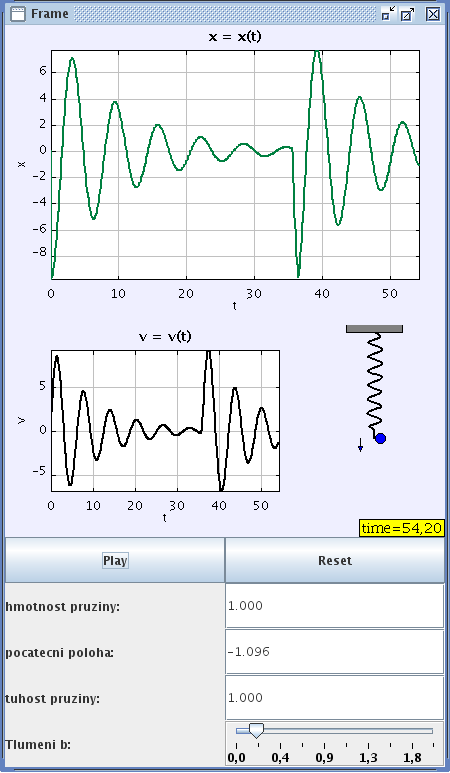
Obr. 4: Možný průběh kmitů
Balistická křivka
Studium šikmého vrhu se započtením odporu prostředí patří k vděčným úlohám – nevyžaduje žádné pojmy nad rámec středoškolské fyziky, ale řešení pohybových rovnic analytickou metodou je velmi obtížné a v obecných případech neexistuje vůbec. Zde se omezíme na případ síly odporu prostředí závisející na kvadrátu rychlosti podle Newtonova vzorce. Těleso s kruhovým průřezem o průměru d a hmotnosti m je vrženo pod úhlem α k horizontu počáteční rychlostí v0. Pohybové rovnice můžeme napsat ve tvaru \[ m\frac{d^2x}{dt^2} = -F_{ox}, \quad m\frac{d^2y}{dt^2} = -F_{oy} - mg, \] kde odporová síla je dána Newtonovým vzorcem \[ F_o = \frac{1}{2}c\rho S v^2 ,\] kde c je součinitel odporu závisející na tvaru tělesa, ρ je hustota vzduchu, S je efektivní průřez tělesa (v modelu uvažujeme kruhový průřez \( S=\frac{\pi d^2}{4}\)). Příslušné diferenciální rovnice lze nalézt např. v [4, 7, 9]. V naší ukázce jsme využili možnosti řešit a vykreslovat současně diferenciální rovnice pro více částic (výhodné např. pro modely různých plynů) – srovnáváme tak trajektorie pro různé počáteční úhly zvolené od 0o do 90o postupně po 5o a můžeme porovnat dolet částic s pohybem bez odporu vzduchu (obr. 5). Proměnné polohy i rychlosti pak ovšem musíme zavést jako vícerozměrné pole. U této úlohy je již výhodou znalost některých příkazů jazyka Java (lze si nechat napovědět EJS). Chceme-li např. úhel α zadávat ve stupních, musíme je pro výpočet převést na radiány funkcí Math.toRadians(). Podobně goniometrické funkce musíme zadávat jako Math.sin()resp. Math.cos(), konstantu p jako Math.PI() atd. Složitější vztahy mezi proměnnými pak zapisujeme do položky „Model/Fixed relations“ (nebo „Model/Constraints“ ve starších verzích EJS). Lze sem dopsat i různé podmínky typu if(){}else{}, při jejichž splnění či nesplnění se např. může pozastavit běh simulace (příkaz _pause()). Jednotlivé příkazy ukončujeme v takovém výpisu středníkem.
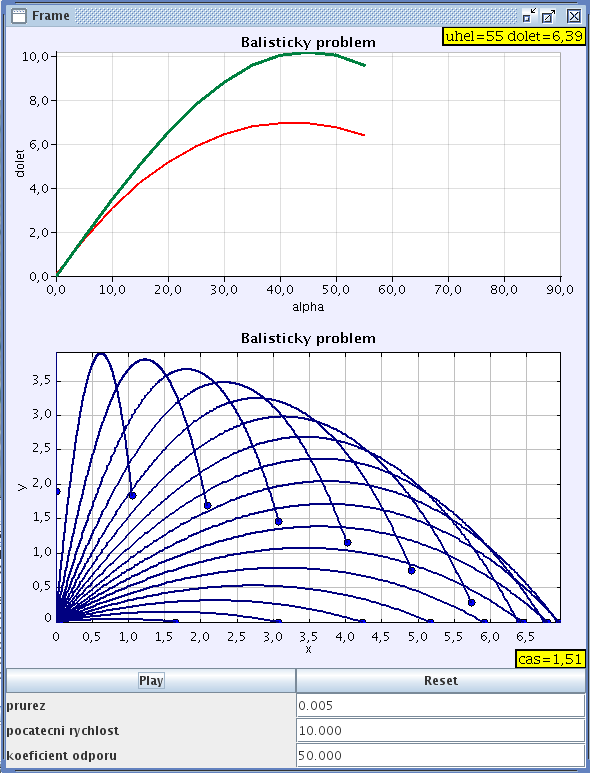
Obr. 5: Balistické křivky
Omezený problém tří těles
V tomto případě jde o úlohu evidentně překračující rámec středoškolské fyziky; zařazujeme ji zde pouze jako ilustraci dalších možností programu, s nimiž jsme se stihli seznámit. Omezeným problémem tří těles označujeme řešení pohybu hmotného tělesa gravitačním poli dvou dalších těles, jejichž hmotnosti jsou mnohem větší než hmotnost naší částice a proto se tato dvě tělesa pohybují po kružnicích okolo svého společného těžiště s úhlovou frekvencí danou Keplerovými zákony. Pohybové rovnice pro naši studovanou částici jsou uvedeny např. v [1] a v soustavě otáčející se s oběma těžšími tělesy zahrnují kromě gravitačních sil také síly Coriolisovu a odstředivou. V naší simulaci (obr. 6) modelujeme jak pohyb tělesa v této soustavě (vlevo), tak pohyb všech tří těles z hlediska nerotující inerciální soustavy (vpravo). Využíváme také možnosti barevného znázornění skalárního pole včetně ekvipotenciálních ploch („vrstevnic“), v tomto případě pro zobecněný potenciál zahrnující gravitační a odstředivou sílu, jež nezávisejí na rychlosti. Velmi názorně tak lze ilustrovat polohu dvou z pěti Lagrangeových libračních bodů, v nichž za určitých podmínek splněných např. pro planety naší sluneční soustavy částice setrvává vzhledem ke Slunci a planetě ve stejné poloze, proto se v případě Země využívají pro polohy některých satelitů (podrobněji viz např. [1]).
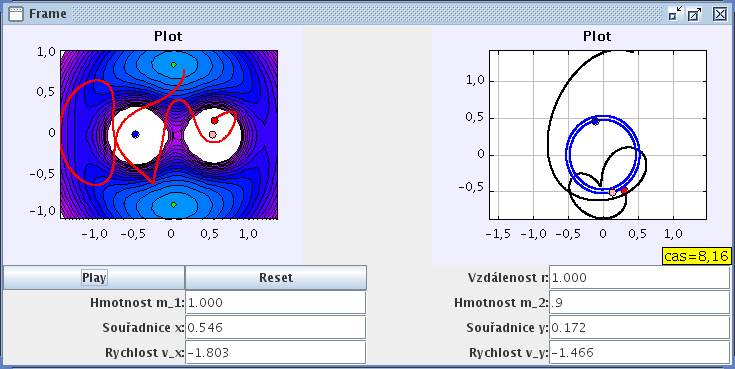
Obr. 6: Omezený problém tří těles
Lissajousovy obrazce
Jako poslední uvádíme známý a vděčný příklad skládání kmitů v kolmých směrech, jež vede k obrazcům pozorovaným francouzským matematikem Julesem Antoinem Lissajousem (1822–1880). Protože k jejich získání nepotřebujeme diferenciální rovnici (i když ji samořejmě sestavit lze), chtěli jsme upozornit, že EJS lze použít i zobrazení časové závislosti veličin daných známými funkcemi, v tomto případě goniometrickými. Zvolit můžeme různou počáteční inicializaci, např. potažením částice myší do zvolené polohy a dopočtením počátečních fází nebo naopak zadáním počátečních fází a odpovídajícím dopočtením počáteční polohy. S jistou omezenou přesnotí pak můžeme odečítat souřadnice i během pohybu, doplnit simulaci zobrazením uplynulého času apod. – čtenáři určitě sami přijdou na řadu zlepšení, která jsme opomněli.
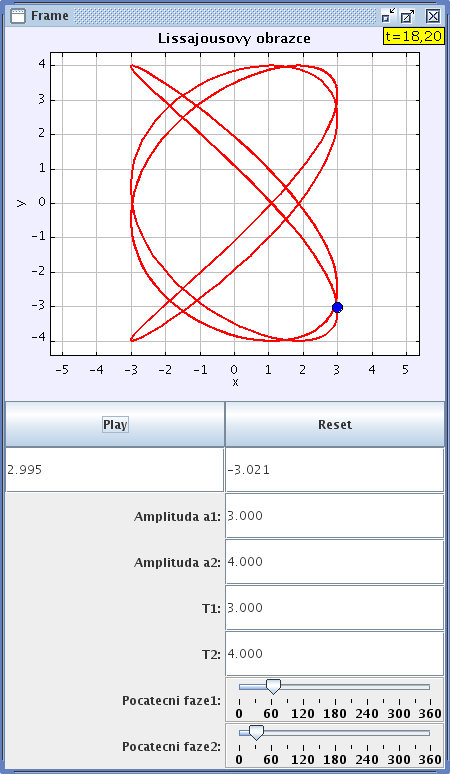
Obr. 7: Lissajousův obrazec
Závěr
Jako u většiny programů, také v případě EJS platí, že každý zájemce se s nimi nejlépe seznámí na konkrétních příkladech, při vlastním „hraní“ si se softwarovým prostředím. Zdrojové soubory ke všem zmíněným simulacím zájemcům rádi zašleme elektronickou poštou a po dokončení bakalářské práce spolu s dalšími zveřejníme na internetu. Z vlastní zkušenosti můžeme potvrdit, že s EJS lze dosáhnout uspokojivého výsledku poměrně brzy a radost z vlastního appletu opravdu stojí za vynaložený čas i námahu.
Literatura
[1] Bajer J.: Mechanika 2. UP Olomouc 2004.
[2] Easy Java Simulation website, http://www.um.es/fem/Ejs/.
[3] GNU General Public License, http://www.gnu.org/licenses/gpl-3.0.html.
[4] Holíková L.: Použití numerických metod v úlohách středoškolské fyziky, Diplomová práce, UP Olomouc 2006, http://optics.upol.cz/richterek/doku.php?id=vyuka.
[5] Christian W., Esquembre F.: „Modeling Physics with Easy Java Simulations“. Phys. Teacher 45 (2007), s. 475.
[6] Christian W., Esquembre F.: Introduction to Easy Java Simulations a EJS and Java Concepts. In Modeling Science: From Free Fall to Chaos. Dosud nevydáno, aktuální verze k dispozici na http://www.compadre.org/Repository/document/ServeFile.cfm?ID=7306&DocID=479.
[7] Lepil O., Richterek L.: Dynamické modelování. Repronis, Ostrava 2007, http://optics.upol.cz/richterek/doku.php?id=vyuka.
[8] Open Source Physics website, http://www.opensourcephysics.org/ nebo http://www.compadre.org/osp/.
[9] Šedivý P.: Modelování pohybů numerickými metodami. Knihovnička FO č. 38, Gaudeamus, Hradec Králové 1999, http://fo.cuni.cz/texty/modelov.pdf.
[10] Urquia A., Martin-Villalba C.: Virtual-lab implementation with EJS. Free online course in: Application in Education, and System Design Analysis, http://www.euclides.dia.uned.es/simulabpfp/curso_online/cursoOnline_content_overview.htm.