O příspěvku
Jednoduché pokusy z optiky
Úvod
Optika patrí medzi tie časti fyziky, ktoré študenti celkom obľubujú. Príčinou môže byť jednak skutočnosť, že s mnohými javmi sa stretávajú aj v bežnom živote, ale aj to, že mnohé z nich možno demonštrovať pomocou jednoduchých pokusov. Ide však o to, aby sa naučili tieto javy vnímať a správne ich pochopiť. K tomu môže prispieť netradičný prístup k prezentácii jednotlivých pokusov formou kúziel alebo využitie medzipredmetových vzťahov, konkrétne poznatkov z matematiky či biológie.
Kúzlo fyziky alebo fyzika kúziel?
Mnohé z uvedených pokusov nie sú nové, za nový však možno považovať popísaný spôsob ich prezentácie v podobe kúziel. Skúsenosť ukazuje, že tento prístup vzbudzuje pozornosť a záujem študentov a zároveň ich zapojenie do vyučovacieho procesu.
Sviečka horiaca pod vodou
Cieľom pokusu je preskúmať vlastnosti obrazu vytvoreného rovinným zrkadlom.
Pred dobre vyleštenú sklenenú dosku, ktorú upevníme v zvislej polohe na stole postavíme pohár do ktorého umiestnime sviečku. Rovnaký pohár umiestnime na opačnú stranu sklenenej dosky a to do rovnakej vzdialenosti, ako sme postavili pohár so sviečkou. Experiment situujeme tak, aby platňa aj poháre boli umiestnené priamo oproti študentom. Potom zahalíme sklenenú dosku tmavou látkou. Zapálime sviečku v pohári pred platňou a predstierame zapálenie sviečky aj v pohári za ňou. Odstránime tmavú látku, vyslovíme „magické slovo“ a naplníme pohár za platňou vodou. Študenti vidia, že v zadnom pohári svieti sviečka pod vodou. Vyzveme študentov, aby sa pokúsili objasniť ako „kúzlo“ funguje. Pri hľadaní vysvetlenia im môžeme pomôcť nasledovnými otázkami: Je možné, aby horela sviečka pod vodou? Aký je obraz sviečky vytvorený rovinným zrkadlom – skutočný alebo neskutočný? Je obraz priamy alebo prevrátený? Aká je veľkosť obrazu v porovnaní s veľkosťou sviečky? Je obraz pred zrkadlom alebo za zrkadlom? Je obraz v zrkadle stranovo obrátený alebo nie? Ak majú študenti problémy s odpoveďami na tieto otázky, je dobré ak máme k dispozícii vhodné rovinné zrkadlo. Nakoniec položíme otázku: Môže sklenená platňa plniť funkciu zrkadla, aké vlastnosti skla to umožňujú? Pomocou týchto otázok privedieme študentov k správnemu vysvetleniu predvedeného „kúzla“. Sklenená platňa plní úlohu rovinného zrkadla vytvárajúc neskutočný obraz horiacej sviečky v pohári za platňou. Hoci sklenená platňa odráža len 4-8% svetla od sviečky stačí to na vytvorenie jasného a presvedčivého obrazu. (Efekt je presvedčivejší ak je svetlo v miestnosti stlmené).
Kúzelná lyžica
Cieľom pokusu je porovnať vlastnosti obrazu vytvoreného dutým a vypuklým zrkadlom.
Študenti držia v rukách kovové dobre vyleštené lyžice otočené vnútornou stranou k sebe. Vyzveme ich, aby sledovali obraz pred sebou. Pozorujú, že obraz v lyžici je prevrátený. Potom vyslovia „magické slovo“ a rýchlo obrátia lyžicu o 180°. Všimnú si, že obraz, ktorý teraz vidia je priamy. Ich úlohou je vysvetliť náhlu zmenu. Opäť pomocou otázok privedieme študentov k tomu, že lyžica plní úlohu dutého či vypuklého zrkadla. Keď sa pozerajú do jej vnútornej strany, predmet – ich tvár, je ďalej ako stred krivosti daného zrkadla, preto vytvorený obraz je skutočný prevrátený a zmenšený. Po otočení sa pozerajú do vypuklého zrkadla, ktoré vždy vytvára neskutočný a prevrátený obraz a preto tá zmena pri pretočení lyžice.
Premena sadzí na striebro
Cieľom pokusu je sledovať úplný odraz na rozhraní dvoch prostredí s rozdielnym indexom lomu.
Predmet napr. kovovú lyžičku pokryjeme dôkladne sadzami nad plameňom sviečky. Povieme študentom, že budú pozorovať premenu sadzí na striebro a po vyslovení „magického slova“ ponoríme lyžičku do nádoby s vodou. Študenti budú vidieť lesklú akoby striebornú lyžičku. Pomocou otázok privedieme študentov k správnemu vysvetleniu „kúzla“. Povrch lyžičky, ktorý sme začiernili sadzou sa vo vode nezmáča. Na jej povrchu sa vytvorí tenká vzduchová vrstvička. pri vhodnej polohe lyžičky, keď pozorujeme, že sa zmenila na striebornú, sa všetky svetelné lúče dopadajúce na vzduchovú vrstvičku od nej odrážajú. Dochádza k úplnému odrazu na rozhraní vody a vzduchu. Vďaka tomu môžeme pozorovať ponorenú lyžičku ako striebornú. (Sú možné aj ďalšie efektné obmeny tohto pokusu napr. s objavením sa neviditeľného obrazu na tmavom papieri, po jeho ponorení do vody a pod.)
Zakrivený laserový lúč
Cieľom pokusu je pozorovať úplný odraz na rozhraní dvoch prostredí s rozdielnym indexom lomu a pochopiť tak princíp svetlovodivých káblov.
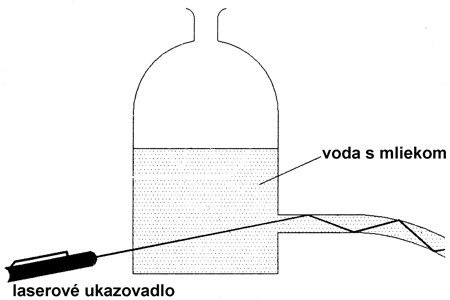
Obr. 1
Vezmeme väčšiu priehľadnú nádobu s malým otvorom blízko dna nádoby. Otvor uzavrieme zátkou a nádobu naplníme vodou, do ktorej sme pridali trochu mlieka. V zatemnenej miestnosti laserový lúč z laserového ukazovadla nasmerujeme tak, aby prechádzal nádobou a dopadal na zátku pri dne. Študentom povieme, že zakrivíme laserový lúč. Vyslovíme „magické slovo“ a odstránime zátku z nádoby. Študenti pozorujú, že laserový lúč sleduje prúd vody vytekajúcej z nádoby (obr. 1) Študentom kladieme otázky: Čo zapríčiňuje, že sa laserový lúč zakriví a zotrváva vnútri vodného prúdu? Aký je index lomu vody v porovnaní s indexom lomu svetla? O aký prechod ide pri prechode svetla z vody do vzduchu? Spoločne tak dospejeme k správnemu vysvetleniu pozorovaného javu. Laserový lúč v prúde vody dopadá na rozhranie medzi vodou – s vyšším indexom lomu a vzduchom s nižším indexom lomu. Keďže uhol dopadu je väčší ako medzný uhol dochádza k totálnemu odrazu a lúč je úplne odrazený späť do vody ako by bol ním zachytený.
Môžeme zároveň pripojiť historickú poznámku, že už v roku 1870 írsky fyzik Tyndall predviedol členom Kráľovskej spoločnosti v Londýne svoj objav úplného odrazu svetla vo vodnom prúde v tvare oblúka. Z pomerov indexov lomu svetla vo vode a vo vzduchu vyrátal medzný uhol. Zistil, že ak svetlo vnútri prúdu vody dopadá na rozhranie voda - vzduch pod väčším uhlom ako je kritický uhol, nemôže z neho vystúpiť von a je v ňom vedené ako v kábli.
Jednoduchý experiment a matematika
Pre lepšie pochopenie a vysvetlenie niektorých javov je dobré doplniť jednoduchý experiment následným matematickým výpočtom. Nasledujúce dva experimenty poskytujú príklad takého spojenia experimentu a výpočtu.
Ako určiť experimentom index lomu vody
Cieľom experimentu je vedieť si uvedomiť podmienky, pri ktorých nastáva lom na rozhraní dvoch optických prostredí.
Keď sledujeme predmet ponorený vo vode priamo zvrchu zdá sa nám akoby plával, teda vidíme ho vyššie ako sa v skutočnosti nachádza. Na stôl umiestnime nádobu naplnenú vodou. Jednu korunovú mincu vložíme do vody, na dno nádoby a druhú na stôl vedľa nádoby s vodou. Pozeráme sa na obidve mince priamo zvrchu (obr. 2) Keď je vonkajšia minca položená na stole (poloha 1) vidíme mincu vo vode väčšiu ako je v skutočnosti, teda ako mincu na stole. Ak budeme mincu mimo nádoby postupne dvíhať, nájdeme polohu (poloha 2), v ktorej má rovnakú veľkosť ako minca vo vode. V dôsledku lomu svetla vo vode sa nám zdá, že minca vo vode je v tejto výške. V našom prípade to bude v 3/4 hĺbky. Prevrátená hodnota tohto čísla, teda 4/3 predstavuje index lomu vody. Ak teda zmeriame hĺbku, v ktorej vidíme ponorený predmet budeme vedieť určiť index lomu vody.
Pri odvodení vzťahu medzi hĺbkou, v ktorej vidíme ponorený predmet, a indexom lomu využijeme vedomosti z matematiky. Zo Snellovho zákona lomu vyplýva:
![]()
Z experimentu aj obr. 3 vyplýva, že uhly α a β budú malé (vzhľadom na veľkosť oka). Ak využijeme vedomosti z matematiky môžeme napísať
![]()
![]()
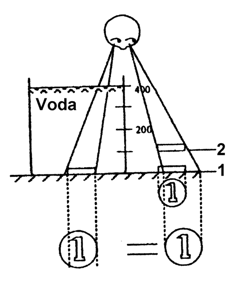
Obr. 2
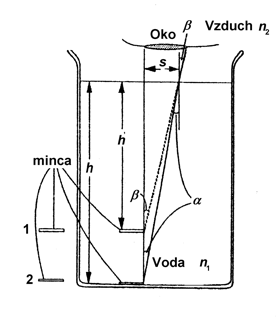
Obr. 3
Keď uvažujeme index lomu pre vzduch
![]()
a dosadíme (2), (3), (4) do (1), dostaneme:
![]()
Teda pomer hĺbky h a h’ nám určuje index lomu vody.
Skrytá figúrka - výpočet veľkosti medzného uhla
Cieľom experimentu je pochopiť úplný odraz a experimentálne aj výpočtom nájsť medzný uhol.
Naplníme akvárium vodou. Zoberieme skúmavku a vložíme do nej napríklad figúrku z hry „Člověče nezlob se“. Ponoríme skúmavku do vody tak, aby sa do nej nedostala voda. Pomaly ju nakláňame a otáčame ňou. Skúmavka sa v jednom okamihu zmení na striebornú a figúrka „zmizne“ – neuvidíme ju.
Voda v akváriu je opticky hustejším prostredím ako vzduch v skúmavke. Otáčaním a nakláňaním skúmavky vlastne hľadáme medzný uhol. Keď sa nám ho podarí nájsť, všetky lúče dopadajúce na skúmavku sa odrazia od opticky redšieho prostredia – vzduchu do nášho oka. Preto sa nemôžeme pozrieť do skúmavky a figúrka ostane pre naším zrakom ukrytá.
Pomocou výpočtu určíme veľkosť hľadaného medzného uhla. Pre medzný uhol dopadu αm platí, že uhol lomu β = 90°. Ak považujeme index lomu vzduchu rovný jednej zo Snellovho zákona lomu vyplýva: n·αm = 1·sin 90°, resp.
![]()
Z rovnice (6) po dosadení za n = 4/3 pre vodu dostaneme: sin αm = 0,75, resp. αm = 48,5°.
Analogicky pre sklo n = 3/2 a αm = 42°.
Úplný odraz sa využíva ako v optických hranoloch, tak v svetlovodných vláknach. Ich základom je tenké sklenené vlákno, ktorého stredná časť má väčší index lomu ako jeho obvodová vrstva a svetelný lúč sa preto v obvodovej vrstve úplne odráža a svetlo sa šíri po trajektórii danej tvarom vlákna.
Jednoduchý experiment a biológia
Ľudské oko, ktoré nám sprostredkúva väčšinu vnemov z okolitého sveta je zároveň optickou sústavou. Pomocou viacerých jednoduchých experimentov môžeme študentom demonštrovať ako časti tejto optickej sústavy zabezpečujú samotné videnie. Tieto experimenty sú zaujímavé ako pre študentov zaujímajúcich sa o fyziku tak pre študentov zaujímajúcich sa o biológiu. Široké možnosti experimentov z tejto oblasti ilustrujeme dvomi príkladmi.
Jednoduchá lupa
Prepichneme kus kartónu (poslúži napr. aj pohľadnica) špendlíkom a urobíme v ňom dierku o priemere asi 1 mm. Kartón s dierkou priblížime k oku a pozorujeme cez dierku písmená v texte. Pri určitej vzdialenosti budeme vidieť písmená ostro a zväčšené. Pomocou špendlíka sme si vyrobili jednoduchú lupu, lebo dierka v kartóne plní jej funkciu. Keď svetlo prechádza malými otvormi alebo okolo malých prekážok, dochádza k ohybu svetelného lúča. V našom prípade sú odklonené lúče odrazené od textu a smerujúce do oka. Výsledkom je zväčšenie písmeniek v texte.
Prevrátený špendlík
Použijeme prepichnutý kartón a špendlík z predchádzajúceho pokusu. Priložíme prepichnutý kartón tesne k oku a potom pred otvor umiestnime špendlík (obrátený hlavičkou hore). V otvore vidíme neprevrátený obraz špendlíka, ktorého veľkosť sa pri približovaní špendlíka k otvoru zväčšuje ale obrysy nie sú ostré. Otvor v kartóne funguje ako dierková komora . Teraz dáme kartón s otvorom asi 5 – 8 cm od oka a špendlík obrátený hlavičkou nahor umiestnite medzi oko a kartón. Pozerajúc sa na dierku, nie na špendlík v otvore spozorujeme obraz špendlíka zväčšený ale obrátený. Vidíme totiž iba tieň špendlíka, ktorý sa na sietnici zobrazuje v tej istej polohe, akú má samotný špendlík – hlavičkou hore. Pretože však naše oko dostáva všetky obrazy na sietnicu obrátene a vďaka mozgu ich chápeme také, aké sú v skutočnosti, tieň špendlíka vidíme obrátene. (Pokus si vyžaduje trochu natrénovať nájsť vhodnú vzdialenosť medzi okom a špendlíkom a pozerať proti svetlu resp. jasnej oblohe.)
Záver
V príspevku sme sa pokúsili prezentovať rôzne spôsoby uplatnenia jednoduchých experimentov vo vyučovacom procese na konkrétnych príkladoch z optiky. Prirodzene existujú aj ďalšie spôsoby ich využitia vo vyučovaní fyziky. Veríme, že uvedené experimenty poslúžia ako inšpirácia a učitelia dokážu prezentované prístupy použiť aj pri vysvetľovaní ďalších fyzikálnych javov.
Literatúra
1. Halada, V.: Fyzika v pokusoch, SPN, Bratislava, 1953
2. Kupka, Z., Hála, J.: Pokusy s laserem, Prometheus, Praha, 1996
3. Pokusy pre malých debrujárov 4, Amavet, Šaľa, 1992
4. Sokoloff, D. R.: The Magic of Physics/The Physics of Magic, GIREP Seminar Ljubljana, Slovenia, 2005
5. Svoboda, E.: Pokusy z fyziky s jednoduchými pomůckami, Prometheus, Praha, 1995