O příspěvku
PDF ke staženíGyrotwister – princip a užití
Před několika lety se na západě začaly v prodejnách sportovních potřeb objevovat zvláštní posilovače rukou. Jsou v prodeji pod názvem „Gyrotwister“, „Dynabee“, „Power ball“ apod. Malý přístroj, připomínající hračku, je založen na dynamické reakci roztočeného setrvačníku.
Vhodným krouživým pohybem ruky se může počet otáček setrvačníku zvýšit až na 12 000 ot/min.
Princip tohoto přístroje vychází z amerického patentu, který si podal v roce 1973 Archie L. Mishler . O několik let později našlo toto zařízení cestu do obchodů. Později došlo ke zdokonalení tohoto zařízení. Jedním z nejvýznamnějších doplňků byl malý elektrický generátor, který napájí několik svítivých diod.
Pohled na přístroj a obrázek z patentního spisu vidíme na obr.1.(převzato z [1] )
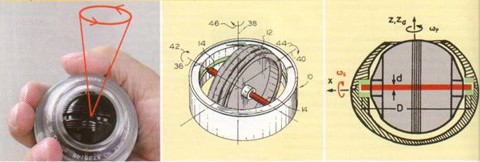
Obr. 1: a - vlevo, b - uprostřed, c - vpravo
Na obr.1a vidíme celkový pohled na přístroj. Obr.1b ukazuje princip přístroje podle amerického patentu. Vidíme, že setrvačník je nasazen na delší ose, která se může volně pohybovat v drážce pouzdra. Přístroj v řezu je znázorněn na obr.1c. Vlastní úhlová rychlost setrvačníku je označena 
. Vynucená precese vyvolávaná pohybem ruky má úhlovou frekvenci 
. Drážka má poněkud větší výšku než je průměr d osy setrvačníku, jak je dobře vidět z obrázku 1c.
Vysvětlení na základě dynamiky setrvačníku vychází ze základní pohybové rovnice pro rotaci tuhého tělesa. Podle ní je časová změna momentu hybnosti 
rovna působícímu výslednému momentu sil [2]:
Není-li moment síly příliš velký, spočívá odezva setrvačníku v jeho precesním pohybu, jak je patrno z obrázku 2. Zde 
. ( J je moment setrvačnosti vzhledem k ose setrvačníku). Jestliže se výrazně nemění poloha okamžité osy v tělese (což je v našem případě splněno), reaguje setrvačník na působení vnějšího momentu precesním pohybem, jehož úhlová frekvence vyhovuje vztahu
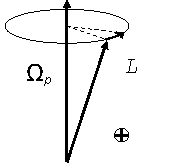
Obr. 2
Vztah (2) můžeme ovšem chápat také tak, že vynucená rotace s úhlovou rychlostí vyvolá moment 
. To je vlastně tvrzení Foucaultovy věty, podle níž [3] roztočený setrvačník s momentem hybnosti , který je nucen vykonávat další rotaci 
( není rovnoběžné s ), je podroben momentu, jenž působí tak, aby obě osy rotace byly souhlasně rovnoběžné. Vzniklý moment přitiskne osu setrvačníku ke stěně drážky, jak je zakresleno na obr.3. Pouzdro se otáčí úhlovou rychlostí . Tření mezi osou setrvačníku a drážkou způsobí, že setrvačník získá dodatečnou úhlovou rychlost
kde D je střední průměr drážky (obr. 1c) a d je průměr osy. Jestliže Δω < ωs nastává urychlování rotace setrvačníku. V opačném případě by byl setrvačník přibržděn. Vztah (3) můžeme přepsat i pro počty otáček za minutu ve tvaru
.
Změna směru vynuceného otáčení nemění výsledné působení na zvyšování otáček vlastní rotace setrvačníku. Proto je možné procvičovat obě ruce v obou směrech otáčení.
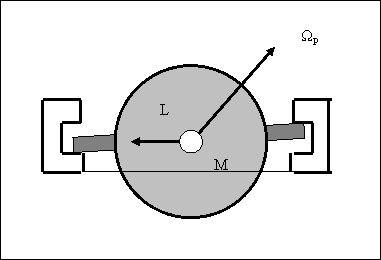
Obr. 3
Uvažujme, že D ≈ 50 mm, d ≈ 2 mm. Jestliže přístroji udělíme rukou 5 otáček za sekundu, tj. np= 300 ot/min, bude ΔN = 7500 ot/min. Potřebný moment síly je značný a výrobci uvádějí, že síla nutná na udržení vynucené rotace přístroje dosahuje až 180 N. Uvádí se, že přístroj může být užit i k terapeutickým účelům.
Počáteční rotace se setrvačníku uděluje zpravidla pomocí šňůrky , která se navine do drážky na obvodu setrvačníku. Je nezbytné, aby počáteční hodnota ωs byla větší než určitá kritická hodnota. Jen za této podmínky je moment hybnosti a tím i vznikající moment M dosti velký, aby mezi osou setrvačníku a drážkou pouzdra působilo tření potřebné velikosti. Je též zajímavé, že dosažení vysokého počtu otáček vyžaduje jistou synchronizaci pohybu ruky. Ne každému se podaří roztočit Gyrotwister napoprvé. Také pokus nahradit pohyb ruky otáčením pouzdra na odstředivém stroji nevedl ke kladnému výsledku.
Cena Gyrotwisteru, zakoupeného v SRN se pohybuje v rozmezí 500-600 Kč. Jde o zařízení, které vtipným způsobem využívá vlastností setrvačníku a může ve školské fyzice posloužit při motivaci žáků.
Literatura.
[1] Ucke, Ch., Schlichting, H.J.: Faszinierendes Dynabee, Physik in unserer Zeit, 5/2000, s.230-231
[2] Klimeš, B. a kol. : Základy fysiky I, NČSAV, Praha 1962
[3] Záviška, F.: Mechanika, JČMF, Praha 1933