O příspěvku
Elektrostatický „mlynček“
Na príklade tohto jednoduchého experimentu je možné ukázať, že ak chceme kvantitatívne a kvalitatívne vysvetliť fyzikálny jav z oblasti modernej fyziky (kvantovej fyziky alebo fyziky častíc), hoci na stredoškolskej úrovni, vždy k tomu potrebujeme veľmi dobrý základ z mechaniky, molekulovej fyziky, elektriny a magnetizmu. Tieto časti klasickej fyziky stále tvoria základnú platformu fyzikálneho vzdelávania. Preto je treba hľadať ďalšie fyzikálne javy, ktoré je možné vysvetliť pomocou fyziky strednej školy a tak vytvoriť aj ich matematický model. Výhodnou je ak môžeme daný fyzikálny jav demonštrovať experimentom, poprípade získať z neho súbor dát.
Pomôcky: elektricky izolovaný stojan s hrotom, elektrostatický „mlynček“ (obr. 1), zdroj elektrostatického napätia, napr. Wimshurstova indukčná elektrika, stopky, spojovacie vodiče.
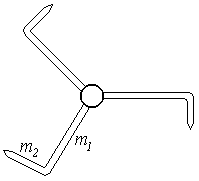
Obr. 1
Príprava a realizácia: Na stojan s hrotom položíme elektrostatický „mlynček“ tak, aby sa mohol voľne otáčať. Pomocou stojana privedieme na „mlynček“ vysoký elektrický potenciál záporného znamienka zo zdroja elektrostatického napätia, napr. z Wimshurstovej indukčnej elektriky a pozorujeme, že „mlynček“ sa začína roztáčať. Pomocou stopiek zmeriame časovú závislosť zmeny polohy jedného ramienka roztáčajúceho sa „mlynčeka“ tak, aby sme mohli určiť jeho uhlové zrýchlenie, o ktorom na základe pozorovania predpokladáme, že je zo začiatku konštantné (obr. 2). Experiment môžeme opakovať s „mlynčekom“ nabitým na opačný potenciál.
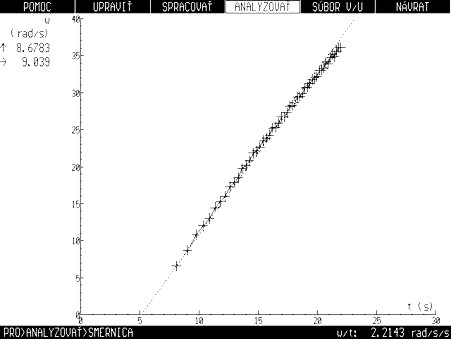
Obr. 2. Graf závislosti uhlovej rýchlosti otáčania sa elektrostatického „mlynčeka“ od času, nameraný pomocou optickej brány so systémom IP-Coach. Z grafu vyplýva, že uhlové zrýchlenie je zo začiatku konštantné a má hodnotu 2,2 rad/s2.
Vysvetlenie: Ak je „mlynček“ nabitý na záporný potenciál, z hrotov na konci ramien „mlynčeka“ srší náboj – unikajú z nich elektróny a v dôsledku zákona zachovania hybnosti sa mlynček začne otáčať. Ak je „mlynček“ nabitý kladne, ionizované molekuly vzduchu, ktoré sa v ňom vždy v istom počte nachádzajú, v dôsledku veľkého gradientu potenciálu elektrického poľa v blízkosti hrotov sú natoľko urýchľované, že dochádza k ionizácii ďalších molekúl nárazom a počet voľných elektrónov takto stačí na to, aby po náraze na hrot mohli roztočiť „mlynček“.
V súvislosti s týmto experimentom je možné žiakom položiť niekoľko kvalitatívnych aj kvantitatívnych otázok. Napríklad:
1. Skôr ako pripojíme „mlynček ku kladnému potenciálu konštatujeme, že je logické, že „mlynček“ sa otáča, ak je nabitý záporne, no bude sa otáčať aj keď je nabitý kladne? Na ktorú stranu?
2. Bude sa „mlynček“ otáčať aj vo vákuu?
3. Z kvantitatívnych otázok je zaujímavý odhad počtu elektrónov, ktoré musia naraziť na hrot „mlynčeka“ za jednu sekundu, na stredoškolskej úrovni.
Odhad je možné urobiť pomocou pohybovej rovnice roztáčajúceho sa „mlynčeka“,
N M = J α,
kde N predstavuje počet narážajúcich elektrónov, M je moment sily od dopadajúceho elektrónu,
![]() ,
,
kde me je hmotnosť elektrónu, ve je rýchlosť elektrónu, r je dľžka ramena mlynčeka, √2/2 je geometrický koeficient zohľadňujúci, že elektróny nenarážajú na hrot kolmo, ale z rôznych smerov a pohybový účinok pre „mlynček“ má len zmena zložky hybnosti elektrónu v kolmom smere (obr. 3). J je moment zotrvačnosti „mlynčeka“ J = J1 + J2, J1 = ⅓ m1∙r2, J2 = m2∙r2, α je uhlové zrýchlenie „mlynčeka“, α = Δω/Δt.
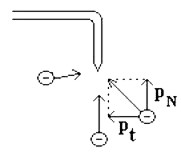
Obr. 3
Rovnicu (1) môžeme teda prepísať na tvar:
![]() ,
,
Z rovnice (2) môžeme vyjadriť počet elektrónov N:
![]()
Všetky hodnoty okrem ve sú známe alebo ich zistíme meraním pre konkrétny „mlynček“. Rýchlosť dopadajúcich elektrónov odhadneme pomocou vzťahu
![]() .
.
Problémom zostáva odhadnúť urýchľujúci potenciál U. Vzhľadom na to, že urýchľované elektróny sa neustále zrážajú s molekulami vzduchu, pri niektorých zrážkach strácajú časť svojej energie. Jedná sa najmä o tie zrážky, pri ktorých má elektrón dostatočnú energiu na ionizáciu molekuly. Keďže dva prevládajúce plyny vo vzduchu N2 a O2 majú ionizačnú energiu 14,5 eV, resp. 13,6 eV, väčšiu energiu urýchlený elektrón vo vzduchu nemá šancu získať, lebo ju vždy stratí po zrážke s takouto molekulou. Strednú hodnotu urýchľujúceho napätia teda môžeme odhadnúť na 7 V. Maximálna rýchlosť pre dopadajúce elektróny potom je 1,6∙106 ms-1.
Z rovnice (3) pre hodnoty odpovedajúce nášmu „mlynčeku“ vychádza N = 2,0∙1020 dopadajúcich elektrónov na jeden hrot „mlynčeka“ za sekundu.
Zoznam použitej literatúry:
[1] Fuka J., Havelka B. : Elektřina a magnetismus. SPN Praha, Praha 1979.
[2] Čičmanec P. : Elektrina a magnetizmus. Alfa Bratislava, Bratislava 1980.