Souhrnný sborník Veletrhu nápadů učitelů fyziky

O příspěvku

PDF ke stažení

Volf I.

Anotace: Experiment je odedávna přirozenou součástí nejen vědeckého výzkumu, ale i základním prvkem názornosti při výuce fyziky. Ve školní praxi slouží k motivaci, získávání základních informací pro výklad i pro aplikaci fyzikálního poznávání. Vedle reálných experimentů mají své místo i ve škole neopakovatelné pokusy historické a v současnosti experimenty virtuální.

Úvodem

Kdybychom psali novou didaktiku fyziky, určitě by se na téma Fyzikální experiment objevilo několik základních tvrzení, jako například:

-  Fyzikální experiment je základní motivační prostředek výuky fyziky. 

-  Bez fyzikálního experimentu si žádný dobrý učitel fyziky nedokáže svou výuku představit.

-  Experiment může poskytnout výchozí motivaci při výuce a probudit zvědavost dětí i jejich touhu po poznání.

-  Experiment může poskytnout data pro výklad a následné vyvození fyzikálních zákonitostí.

-  Fyzikálním experimentem můžeme ověřovat správnost získaných teoretických znalostí nebo navržených hypotéz při řešení fyzikálních problémů.

-  Experiment poskytuje možné aplikace fyziky, a tím potvrzuje užitečnost fyzikální vědy i výuky fyziky pro život člověka v moderní společnosti.

-  Fyzikální experimentování rozvíjí tvořivost žáků na opakovatelných situacích.

-  Pomocí experimentu se rozvíjí jemná motorika žáků při práci s měřicími přístroji.

Vyskytnou se však také všetečné otázky: Je reálný experiment jedinou možnou cestou k fyzikálnímu poznání?  Jak ve škole předvádět fyzikální experimenty, které zdárně proběhly v historii fyziky, ale nejsou ve školní posluchárně fyziky realizovatelné? Je užitečné použít tzv. vzdálené laboratoře, kdy z důvodu neexistence vhodné pomůckové základny přímo na škole experiment probíhá někde v tajemné dálce a žáci ho sledují s komentářem učitele zprostředkovaně na monitoru počítače?

Experiment může být také hodnocen jako zdržování výkladu učitele, neboť při současném spěchu a plnění osnov v omezeném čase není na pokusy dost času. Současně však mají experimenty i ekonomickou složku – ve školství není dostatek finančních prostředků pro to, aby se soustavně doplňovalo vybavení fyzikálního kabinetu; výroba experimentálních souprav v malých počtech je neekonomický i výrobního i obchodního hlediska. Při nesprávném didaktickém využívání může být experiment jen divadlem pro vyplnění času.

Ještě horší přístup spočívá v tom, že některým učitelům je milejší, když žák „umí“ fyziku, než když jí porozumí. Znát vzorečky, jednotky, převádění a řešení typových úloh, jež mohou být ve srovnávacích testech, které poskytují objektivní porovnání jednotlivých žáků nebo i škol, je tedy pro učitele důležitější než řešení tvořivých problémových úloh, navíc pro učitele obtížně hodnotitelných, zejména když pro řešení se použije jednoduchých, ale dobře opakovatelných činností při experimentování s předměty z běžného života.  Dnes zaměříme naši pozornost i na jinou možnou cestu – virtuální experimenty.

Jedno nedělní odpoledne jsem seděl u počítače a napadlo mě, že bych se měl podívat, jak to vypadá v egyptské Hurgadě, kde právě pobýval můj kolega. Pochopitelně jsem ho na mapách (tedy na satelitním snímku) nenašel, ale když jsem už „byl v Egyptě“, zdálo se mi, že tuto zemi poněkud podrobněji „prozkoumám“, Tím jsem se dostal k řece Nil a také do města Aswan, známého ve starověku jako Syena. A úkol byl jasný: Vzpomněl jsem si, že v těchto místech se řešil problém, jak stanovit rozměry Země, tedy přesněji stanovit poloměr kulové Země. Ze starověku je známo právě měření Eratosthenovo, které se uskutečnilo ve 2. století před naším letopočtem a které je na tuto dobu zcela geniální. Na obrázku vidíme středový úhel φ mezi „polohovými vektory“ míst A(lexandria) a S(yena), který je roven úhlu dopadu slunečního paprsku Alexandrii ve stejném okamžiku, kdy v Syeně dopadaly paprsky na dno hluboké studně, tedy Slunce se nacházelo právě v nadhlavníku. Pak stačilo změřit vzdálenost mezi oběma místy a využít známého vztahu, že poledníkový obvod Země k dané vzdálenosti AS je ve stejném poměru jako 360 :  φ. Jak víme, ve starověku měli však jisté potíže se stanovením vzdálenosti obou jmenovaných míst.

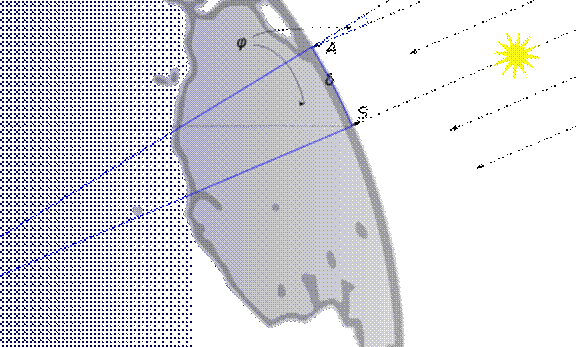
Rozhodl jsem se – když už jsem byl „v prostoru nad Egyptem“, že Erastothenovo měření zopakuji. Použil jsem mapy na www.Googleearth.com. Zjistil jsem však s hrůzou, že obě místa neleží na stejném poledníku, a tak nutně vzniknou ve stanovení identifikačního času drobné nepřesnosti (rozdíl v zeměpisné délce je asi 3°, což představuje rozdíl v okamžiku pravého poledne 12 min = 0,2 h). Zeměpisné souřadnice vzhledem k tomu, že jsem nemohl zcela přesně zjistit počáteční a koncový bod měření, prováděného ve starověku, zaokrouhlíme na úhlové minuty. Údaje pro zvolené místo v Alexandrii jsou 31°09´N, 29°47´E, pro místo v Syeně 23°24´N, 32°47´E. Rozdíl zeměpisných šířek je tedy 7°45´= 7,75°. Na satelitní mapě jsem naměřil vzdálenost 888 km, po vynásobení 360/7,75 vychází pro délku hlavní kružnice 41 250, zjištěný poloměr Země 6 565 km. Výsledek korigujeme přepočtem na eventuální přesnější měření na Alexandrijském poledníku, hledaná vzdálenost je 832 km, délka kružnice 38 647 km, poloměr Země 6150 km; střední hodnota 6 358 km. Výsledek považuji za velmi dobrý.

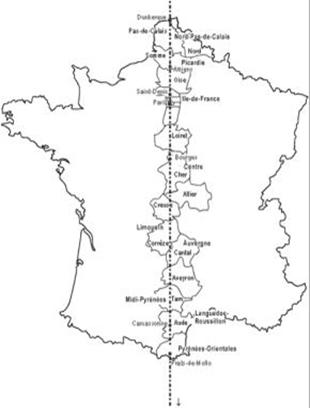
Další zajímavé jsou údaje, získané při definici prvního metru, nové jednotky délky, jež byla zavedena během Francouzské revoluce. Komise Akademie navrhla změřit část délky Pařížského poledníku mezi městy Dunkerque a Barcelona. Vzhledem ke dnes užívanému základnímu poledníku Greenwichskému má Pařížský poledník zeměpisnou délku 2°20´14“ a najdeme ho např. ve staré pařížské astronomické observatoři. K měření oblouku byla využita metoda triangulace, jejíž náčrtek můžeme najít ve více než 100 let staré učebnici Mechanika českého profesora Čeňka (Vincenta) Strouhala, významného fyzika.

Úhlová vzdálenost mezi koncovými body části poledníku, který vede po pevnině po území Španělska a Francie, byla stanovena na 9°40´26“ = 9,67°. Později bylo měření prodlouženo na španělský ostrov Formentera, úhlová vzdálenost se zvětšila na 12°22´13“. K měření byla zvolena jednotka toise de Pérou, bylo naměřeno 705188,8 toise (1 toise byl až do roku 1812 roven 6 stop, po přepočtu 1.949 m). Odtud se propočetl tzv. kvadrant zemský 10 000 000 m, upraveno dalším měřením 10 000 855,76 m s nepřesností ±498,23 m; poloměr zemský potom vychází na 6 367 km. Zajímavě o tomto měření najdeme v knížce Strouhal: Mechanika.

Když už jsem byl v tom měření na satelitních mapách, pokračoval jsem v experimentování. Nejprve bylo třeba najít počáteční a koncový bod měření. Obrátil jsem se nejprve na museum ve městě Dunkerque, ale bez úspěchu, takže jsem zvolil počáteční bod s ohledem na to, že musí ležet na pařížském poledníku a ještě na pevnině, zeměpisná šířka tohoto místa byla 51°03´. Další místo jsem zvolil v okolí Barcelony na břehu moře, v blízkosti pevnosti Mont Joury, zeměpisná šířka 41°29´, rozdíl v zeměpisných šířkách 9°34´, změřená vzdálenost 1062 km, určíme délku kružnice 40 104 km a určený poloměr Země 6380 km. Možná změna změřené vzdálenosti o - 1 km vede k hodnotě poloměru Země 6374 km.

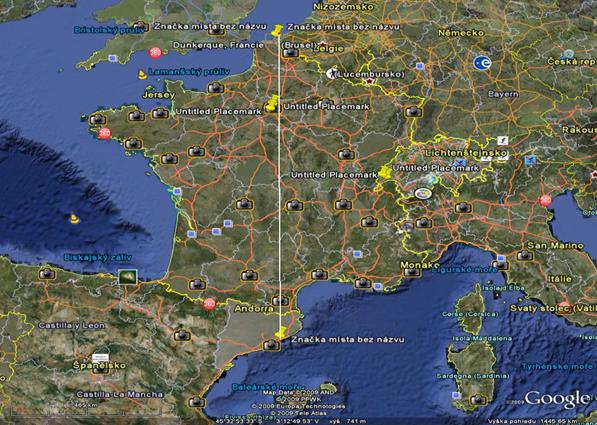
Ke stanovení délky rovníku, nejdelší kružnice na povrchu Země, musíme změřit vzdálenost dvou míst s nulovou zeměpisnou šířkou. To by byl však v minulosti dosti velký problém: Vezmeme-li to z Ekvádoru, z místa Mitad del Mundo, prochází rovník amazonskými nejprve deštnými, leckde dříve zcela neprostupnými pralesy, pokračuje přes Atlantický oceán na africký kontinent, též s neprostupnými pralesy, přechází bouřlivý Indický oceán, přes Sumatru a Borneo pokračuje Tichým oceánem. Takové možnosti, co měla Akademie při měření Pařížského poledníku na evropském kontinentu, zde chybí. Proto jsem použil další možnosti: zvolil jsem si dvě místa na rovníku tak, že začátek měřené délky sledoval místo, kde opouští nulová rovnoběžka indonéský ostrov Sumatra, a dále místo, kde rovník vstupuje na ostrov Kalimantan (Borneo). Z údajů o rozdílu zeměpisné šířky obou míst a změřené vzdálenosti potom lze stanovit rovníkový poloměr Země. Rovník opouští Sumatru v místě daném délkou 103°48´34“E a vstupuje na Borneo v místě daném zeměpisnou délkou 109°10´02“E, takže rozdíl zeměpisných délek asi 5,36°, změřená vzdálenost 596 km, délka rovníku 40 063 km, odtud rovníkový poloměr 6 376 km.

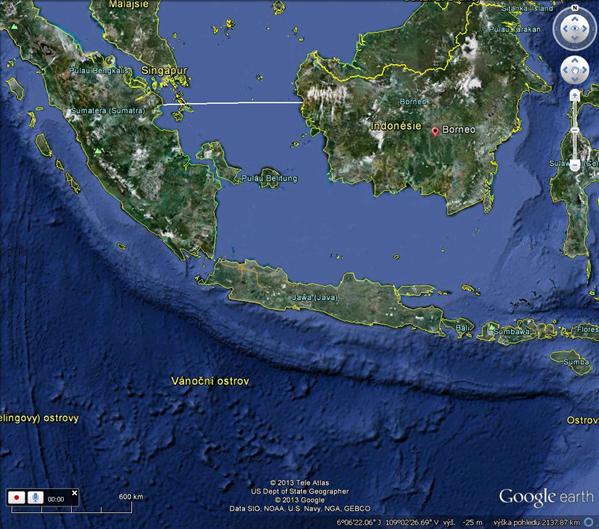
Při měření délky určité rovnoběžky a stanovení jejího poloměru jsem s pomocí satelitních map na www.GoogleEarth.com postupoval takto: Jižně od Berlína jsem zvolil opět dvě místa, ležící na 52. rovnoběžce, o zeměpisných délkách (co nejpřesněji)12° E a 14° E; vzájemná vzdálenost byla změřena 137,5 km. Na jeden stupeň zeměpisné délky pak připadá 68,75 km, délka 52. rovnoběžky mi vyšla 24 725 km, odtud určený poloměr této rovnoběžky 3 935 km. Použijeme-li k výpočtu známých hodnot R = 6371 km a 52° N, vychází hodnota poloměru kružnice výpočtem 3 922 km a délka 52. rovnoběžky 24 645 km. Výsledek našeho měření je tedy poměrně slušný.

Další experiment uskutečněný pomocí internetu a satelitních snímků se týkal měření na témž poledníku. Délku všech poledníků budeme považovat za stejnou, a to jako délku poloviny elipsy, s osami a = 6378,137 km a b = 6356,752 km, délka poloviny elipsy je 20 004 km, na 1° zeměpisné šířky připadá tedy 111,13 km, na 1´ zeměpisné délky 1852,2 km. Dohodou byla stanovena délka námořní míle (nautical mile) 1852 m (přesně), jež vychází z délky kvadrantu 10 000 km. Americká míle byla určena z délky rovníku, tedy délka připadající na změnu 1´ zeměpisné délky, což činí 1855,3 m.

Podívejme se, jak se dají na mapě měřit vzdálenosti na povrchu Země ve směru poledníku.  Při zjišťování vzájemné vzdálenosti různých míst se stejnou zeměpisnou délkou můžeme postupovat takto: Protože jsou všechny poledníky stejně dlouhé (uvažujme přibližně 20 000 km), stačí pro první odhad vzdálenosti využít rozdílu zeměpisných šířek ∆φ a střední hodnoty pro poloměr Země, tj. 6371 km. K přesnějšímu výpočtu potřebujeme znát hodnotu poloměru křivosti rotačního elipsoidu v daném místě. K lepší orientaci budeme označovat místa se severní zeměpisnou šířkou kladně a jižní zeměpisnou šířkou záporně.

Údaje, které nacházíme na internetu, jsou často udávány s přesností na setinu úhlové vteřiny.  Vezměme délku poledníku asi 20 000 km, na 1° připadne asi 111,1 km, na 1´ asi 1852 m, na 1“ asi 31 m, na jednu setinu úhlové vteřiny je to 0,31 m, tedy asi 1 stopa (foot má 30,5 cm). Budeme-li zvažovat měření ve směru některé rovnoběžky, potom jsme zjistili, že na 52. rovnoběžce odpovídá 1° oblouk 71,2 km, pro úhel 1´ odpovídá oblouk 1 187 m, pro úhel 1“ oblouk asi 20 m, jedné setině úhlové vteřiny 0,20 m. Pokusíme-li se vložit měřicí značku (křížek) dvakrát do téhož místa, zjišťujeme poněkud jiné údaje, tedy avizovaná přesnost udávaného měření je větší než je přesnost umisťování měřicí značky.

Jak se měří vzdálenosti na povrchu Země ve směru rovnoběžek? Protože různé rovnoběžky mají různou délku, musíme vždy vědět, o jakou zeměpisnou šířku se jedná. Protože kromě rovníku nejsou rovnoběžky kružnicemi hlavními, nebude vzdálenost dvou míst odměřená po rovnoběžce vzdáleností nejkratší. Vezměme následující případ: Letadlo směřuje z města Valparaiso (33°S, 71,5°W) do Sydney (34°S, 151°E), tedy poletí-li ve směru rovnoběžky, bude rozdíl zeměpisných délek 137,5°) a letadlo urazí trasu 15 270 km. Když poletí po orthodromě, bude vzdálenost míst 11 360 km. Zjišťujeme, že je to podstatný rozdíl, tyto údaje se liší o 3910 km. Podle údajů např. o letadle Boeing 747 lze zjistit, že dolet jistého stroje je 14 800 km a palivové nádrže obsahují nejvýše 243 000 l leteckého kerosínu, odtud odhadneme spotřebu stroje na 16,5 litru na každý kilometr, tedy při letu po orthodromě ušetří letecká společnost celkem 65 500 litrů leteckého kerosinu (úspora na jednom letu činí v CZK více než 2 miliony).   

Při pohledu na globus nebo na mapu polárních oblastí zjistíme, že kontinent Antarktida zabírá přibližně dvě třetiny území, které je ohraničeno jižním polárním kruhem. Využij tohoto poznatku a vypočti povrch Antarktidy. Zemi považuj za ideální kouli s poloměrem 6 371 km.

Nejprve musíme určit výšku x vrchlíku, který je určen na kouli polárním kruhem, tedy rovnoběžkou 66,5°. Z obrázku plyne: y = 5845 km. Potom x = 528 km. 

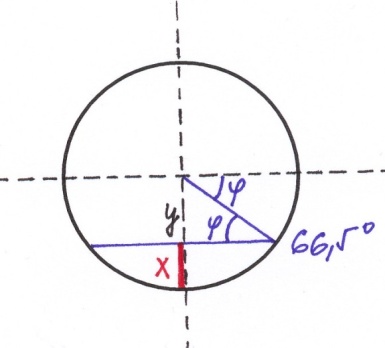
Pro povrch vrchlíku platí:   S = 2π ∙ R_Z ∙ x = 21 135 932 km², přičemž dvěma třetinám odpovídá povrch přibližně 14 000 000 km².

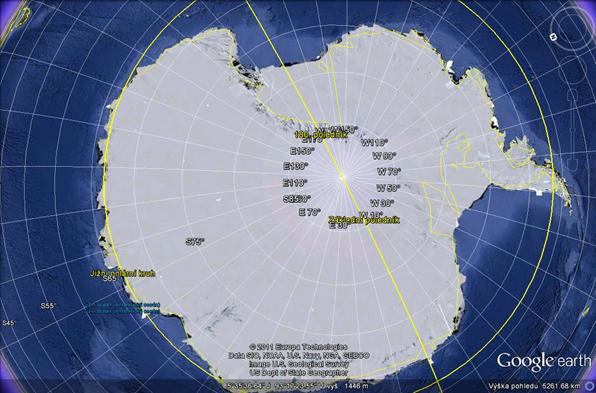
Na základě provedeného měření na satelitní mapě můžeme založit i následující výpočty: Uvažujeme-li průměrnou tloušťku ledu v Antarktidě 2 000 m, je objem ledu roven celkem: 2,8·10¹⁶ m³. Hmotnost ledu je m = r ∙ V = 2,56 ∙ 10¹⁹ kg (hustota ledu  917 kg/m³), jeho roztáním by vznikla voda o objemu V = 2,5 ∙ 10¹⁶ m³ (hustota slané vody 1 028 kg/m³). Pokud by se voda rozlila rovnoměrně po povrchu Země (povrch Země je 510 ∙ 10⁶ km², oceány zaujímají 71 % povrchu, tj. 362 ∙ 10⁶ km²), znamenalo by to zvýšení hladiny světového oceánu o 70 m. Byla by zaplavena rozsáhlá pobřežní území, mnohé ostrovní státy by z mapy světa zmizely úplně. Podstatně by se také změnila hranice mezi mořem a pevninou. To je však už jiná pohádka.

Ve všech našich úvahách jsme experimentovali; tyto experimenty však neproběhly s reálnými pomůckami. Pracovali jsme s internetem, potřebné hodnoty jsme získávali na satelitních mapách, případně jsme hledali potřebné údaje ve Wikipedii. Na druhé straně jsme však zjistili, že jsme museli postupovat stejně, jako kdybychom dané údaje získali přímým nebo nepřímým měřením. Tak, jako žijí lidé ve virtuálním světě, vytvořeném pomocí počítače a příslušných programů, také my jsme pracovali s virtuálními hodnotami, a to ve virtuálních fyzikálních experimentech. Tak se svět reálné fyziky, jenž děti leckdy ani moc nezajímá a my někdy nedokážeme překročit hranice k dětem, začal podobat světu dětské hry s počítačem. Co když právě toto je cesta ke „zlidštění (pro děti) málo zajímavé fyziky“?

Omlouvám se všem nadšeným experimentátorům, kteří sedí i nesedí mezi námi. Jsem také nadšenec jednoduchých experimentů, vedoucích k rozvoji tvořivosti pomocí pomůcek, které máme nedaleko sebe, aniž bychom věděli, že s nimi lze pokusy provádět. Ale jsem také nadšený pro tzv. historické pokusy – jejich uvádění je první cestou k tomuto virtuálnímu experimentování: zobrazujeme a vysvětlujeme experimentální soupravy, používáme dříve získaných údajů. Internet nám dává mnoho možností pro historii fyziky. Proč tedy nenacházet na internetu a v encyklopediích údaje o realitě, jež nám poskytnou další možnosti pro virtuální pokusy?

Odkazy na literaturu:

Volf, I.: Jak jsem měřil (na) zeměkouli. Matematika-Fyzika-Informatika  2012, č. 7.

Volf, I., Kabrhel, P.: Několik reálných a virtuálních experimentů. Matematika-Fyzika-Informatika (2013, č. 5).

Volf, I.: Pedagogické aplikace modelování reality (rukopis materiálů jako učební opory pro doktorské studium informatiky).

Volf, I., Jarešová, M.: Fyzikální úlohy řešené kvalifikovaným odhadem. http://cental.uhk.cz.

Volf, I., Klapková Dymešová, P.: Na rozhraní fyziky a zeměpisu. http://cental.uhk.cz.

Volf, I., Klapková Dymešová, P.: Jak měříme vzdálenosti měst na mapách povrchu Země. Rozhledy matematicko-fyzikální 88 (2013), č. 3, s. 30-35

Volf, I.: Několik úvah o experimentování ve výuce fyziky. MAFY 1997.

Volf, I., Kabrhel, P.: Fyzikální úlohy v 1., 2. a 3. kole Fyzikální olympiády. Volně přístupné i s řešením na http://fyzikalniolympiada.cz 

Obrázky použity z Wikipedie.