O příspěvku
PDF ke staženíLidské tělo jako předmět fyzikálního měření
Abstrakt
Laboratorní práce by měly být nedílnou součástí výuky fyziky. Vyučující se však často setkávají s nedostatkem pomůcek a nezájmem ze strany žáků. Jak lze tedy provést laboratorní práce snadno, zábavně a s využitím poutavého příběhu? Nechte žáky vypravit se například po stopách zločinu a vypátrat pachatele či vyzkoušet si praktiky očního lékaře.
Laboratorní práce na téma optika
V dnešní době nejsou brýle u člověka nic neobvyklého, alespoň na čtení je používá již značná část populace. Každý tedy ví, že čočky brýlí jsou charakteristické především svou optickou mohutností udávanou v dioptriích, ať kladných či záporných. Vědí však studenti jaká je vlastní optická mohutnost oka? Jak vzniká v oku obraz? Jak je možné, že člověk vidí ostře na blízko i na dálku? Nechme je si to vypočítat, případně změřit pro své vlastní oči v rámci laboratorní práce.
Optická soustava lidského oka
Zeptáme-li se studentů na informace týkající se lidského oka, často nejsou ani schopni říci jeho správné rozměry, natož optickou mohutnost. Nosí-li například někdo brýle s pěti dioptriemi, pokládají to studenti již za značnou optickou mohutnost. Co tedy řeknou, zjistí-li přibližnou optickou mohutnost svého oka? Zkusme nejprve optickou mohutnost oka vypočítat pomocí modelu, a následně změřit.
Existuje několik modelů lidského oka, které umožňuji poměrně přesný, ale zjednodušený popis zobrazování předmětu okem. Pro naše účely použijeme kombinaci Gullstrandova modelu a Emsleyova-Graffova schematického modelu oka. [1]
Při vytváření obrazu musí světelný paprsek projít až k sítnici, místu vytvoření obrazu, čtyřmi různými optickými prostředími. Těmito prostředími jsou rohovka, komorová voda, čočka a sklivec. Každé z nich má odlišné optické vlastnosti, které si budeme nyní charakterizovat pomocí průměrných hodnot zdravého oka.
Rohovka má tvar vypukloduté čočky a lze ji popsat těmito parametry:
| Poloměr křivosti vnější plochy | r1 = 7,7 mm |
| Poloměr křivosti vnitřní plochy | r2 = 6,8 mm |
| Index lomu rohovky | nr = 1,376 |
| Tloušťka rohovky | dr = 0,5 mm |
Komorová voda vyplňuje přední oční segment o hloubce zhruba 2,7 mm.
| Index lomu | nkv = 1,336 |
Oční čočka funguje v oku jako spojná čočka. Lze jí charakterizovat podobně jako lupu – nablízko zvětšuje, na dálku kreslí zmenšené převrácené obrázky. Zrak využívá pouze tuto druhou vlastnost. Zakřivení oční čočky není stejné na obou stranách, přední plocha je méně vyklenutá než zadní. Čočku lze tedy popsat parametry:
| Poloměr zakřivení přední plochy čočky | R1 = 10 mm |
| Poloměr zakřivení zadní plochy čočky | R2 = −6 mm |
Index lomu čočky nemá stejnou hodnotu v jejím jádru a na okraji, ve výpočtech se používá průměrná hodnota nč = 1,416
Rosolovitá hmota sklivce vyplňuje celý zadní segment oka. Sklivec charakterizujeme pouze jeho indexem lomu, který je stejný jako v případě komorové vody.
| Index lomu sklivce | ns = 1,336 |
Optickou soustavu oka si lépe představíme za pomoci následujícího nákresu.
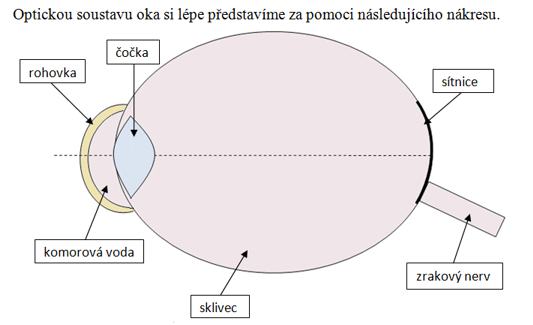
Nákres 1 – Optické složky oka
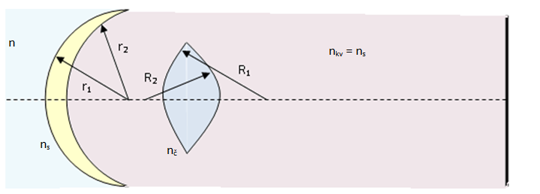
Nákres 2 – Zobrazovací systém oka
Na začátku laboratorní práce se můžeme žáků zeptat, co všechno znají o lidském oku, a s jejich pomocí vytvořit nákres podobný nákresu č. 1. Zjistíme, zda žáci vědí, které části lidského oka tvoří zobrazovací aparát a jak vlastní obraz v oku vzniká.
Při zjišťování částí tvořících optickou soustavu oka kreslíme nákres č. 2, jenž poslouží jako model pro následující výpočet optické mohutnosti oka.
Výpočet optické mohutnosti oka
Optickou soustavu oka rozdělíme na dvě části – rohovku a oční čočku.
Rohovka je zhruba 0,5 mm silná vypuklodutá čočka z jedné strany obklopená vzduchem a z druhé strany komorovou vodou. Pro výpočet její optické mohutnosti použijeme rovnice pro tlustou čočku.
Pod pojmem tlustá čočka, respektive jen čočka rozumíme dvojici centrovaných lámavých kulových ploch o určitém indexu lomu, vnořených do prostředí o různých indexech lomu.
Tlustá čočka je jednoznačně zadaná indexy lomu, parametry obou kulových ploch (středy S a poloměry r) a vzdáleností jejich vrcholů d. Tlustá čočka je v podstatě složená centrovaná zobrazovací soustava, dílčími zobrazovacími soustavami jsou obě lámavé kulové plochy. [2]
Optická mohutnost čočky je rovna převrácené hodnotě ohniskové vzdálenosti čočky, tedy \(\varphi = \frac{1}{f}\). Proto musíme nejprve určit ohniskovou vzdálenost rohovky jako celku. Vyjdeme z následujících vztahů pro tlustou čočku [2]: \[ f = \frac{f_1 f_2}{\Delta} .\]
Pro ohniskové vzdálenosti jednotlivých lámavých ploch rohovky platí:
\[ f_1 = - \frac{n r_1}{n_r - n}, \qquad f'_1 = - \frac{n_r r_1}{n_r - n}, \] \[ f_2 = - \frac{n_r r_2}{n_{kv} - n}, \qquad f'_2 = - \frac{n_{kv} r_2}{n_{kv} - n_r}. \]Pro optický interval tlusté čočky platí následující vztah:
\[ d = f'_1 + \Delta - f_2 .\]Po dosazeních a následných úpravách dostaneme vztah pro optickou mohutnost rohovky ve tvaru:
\[\varphi_r = - \frac{d(n_r-n)(n_{kv}-n_r) - n_r r_1 (n_{kv} - n_r) - n_r r_2 (n_{r} - n) }{n n_r r_1 r_2} .\]Po číselném dosazení jednotlivých hodnot \( \varphi_r = 43\,D\).
Obdobně budeme postupovat i v případě oční čočky, kdy se však jedná o dvojvypuklou čočku obklopenou prostředím o stejném indexu lomu. Tím se vypočet značně zjednoduší.
Pro ohniskové vzdálenosti dvou lámavých ploch bude platit [2]:
\[ f_1 = - \frac{n_{kv} R_1}{n_č - n_{kv}}, \qquad f'_1 = - \frac{n_č R_1}{n_č - n_{kv}}, \] \[ f_2 = - \frac{n_č R_2}{n_{kv} - n_č}, \qquad f'_2 = - \frac{n_{kv} R_2}{n_{kv} - n_č}. \]A následně pro optickou mohutnost čočky:
\[\varphi_č = - \frac{(n_{č}-n_{kv})[(n_{č}-n_{kv})d + n_č (R_1 - R_2) ]}{n_č n_{kv} R_1 R_2} .\]Po číselném dosazení je hodnota optické mohutnosti čočky rovna 17,5 D.
Celkovou optickou mohutnost oka získáme pouhým sečtením hodnot rohovky a oční čočky, jelikož uvažujeme, že jsou centrované a těsně na sebe naléhají. Zdravé lidské oko má tedy dle našeho výpočtu 60,5 dioptrií.
Výpočet optické mohutnosti oka pomocí měření konvenční vzdálenosti
Již víme přibližnou hodnotu optické mohutnosti lidského oka, nyní se pokusíme určit tuto veličinu pro naše oči pomocí měření.
Konvenční vzdáleností se myslí vzdálenost předmětu od neakomodujícího oka (nezaostřeného oka), kdy se předmět zobrazuje na sítnici nejostřeji.
Pro tuto úlohu potřebujeme list papíru s tištěným textem běžné velikosti a délkové měřidlo. Měření bude probíhat celkem třikrát – pro pravé oko, levé oko a obě oči současně. Zakryjte si jedno oko a uchopte list papíru s textem do ruky, která je na stejné straně těla jako otevřené oko. Oko nezaostřujte, spíše se pokuste o koukaní do dálky. Přibližujte a oddalujte ruku s textem, dokud naleznete místo nejostřejšího vidění. Změřte vzdálenost mezi tímto místem a okem, jedná se právě o onu konvenční vzdálenost. Měření provedeme i pro zbylé dva uvedené případy.
Pokládejme optický systém oka za jednu spojnou čočku, před kterou je předmět umístěn v konvenční vzdálenosti a obraz se vytváří na sítnici, zhruba 17 mm od této čočky. [1]
Je nutné dát pozor na znaménkovou konvenci. Pokud zapíšeme známé hodnoty, obdržíme:
a = konvenční vzdálenost v metrech (měla by dosahovat hodnot 0,25 – 0,3 m)
a´= 17 mm = 17·10-3 m
Pro výpočet použijeme zobrazovací rovnici čočky: \( \varphi = \frac{1}{a'} - \frac{1}{a}\).
Není překvapením, že každé oko může mít jinou optickou mohutnost.
Měření akomodace oka
Lidské oko je schopné zobrazovat ostře předměty blízké i vzdálené. Vytvoření obrazu předmětu v různé vzdálenosti před okem je umožněno změnou optické mohutnosti uvedeného dioptrického systému oka, tzv. akomodací. Jaký rozsah akomodace v dioptriích lze opět stanovit měřením. Lidské oko rozlišuje dva okrajové body – bod daleký a bod blízký. Bod daleký znázorňuje nejvzdálenější předmět, jenž může ještě oko vidět ostře. Tento bod by se u zdravého oka měl teoreticky nalézat v nekonečnu. Není tedy nutné jej měřit. Naopak bod blízký značí nejblíže oku umístěný předmět, který ještě není rozmazaný. Vzdálenost bodu blízkého budeme měřit. [1]
Opět použijeme papír s textem běžné velikosti, postupně jej budeme přibližovat k oku až do okamžiku, kdy bude text naposledy jasně čitelný. Zde se nachází blízký bod a jeho vzdálenost od oka změříme. Měření můžeme provést opět pro každé oko zvlášť i obě oči současně.
Zjištěnou hodnotu dosadíme do rovnice:
\( \frac{1}{a_d} - \frac{1}{a_b}\) = akomodační amplituda,
kde ab označuje bod blízký a ad bod daleký. Hodnoty dosazujeme v metrech, aby výsledek byl v dioptriích. Jelikož ad je rovno nekonečnu, nabývá druhý zlomek v rovnici hodnoty nula.
Akomodační amplituda se mění s věkem, jak ukazuje následující obrázek.
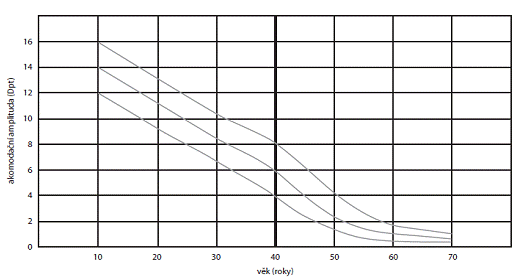
Obrázek 3 – Závislost akomodační amplitudy na věku [1]
Literatura
[1] KUCHYNKA, Pavel. Oční lékařství. 1.vyd. Praha: Grada, 2007, [40], 768 s. ISBN 978-802-4711-638.
[2] KALUS, René. Trivium z optiky. Vyd. 1. Ostrava: Ostravská univerzita, 2004, 107 s. ISBN 80-704-2999-2.