O příspěvku
PDF ke staženíJednoduché experimenty s gumou a kuličkodráhou
Abstrakt
Návrh na využití hračky s názvem Kuličkodráha ve výuce fyziky a několik jednoduchých experimentů s polymery – gumou, kterými lze doplnit a zpestřit výuku termodynamiky.
Úvod
Ve výuce fyziky se snažíme motivovat své žáky využitím nejrůznějších metod a prostředků, které ve výuce používáme. Snažíme se používat jednoduché pomůcky, se kterými se žák setkává v každodenním životě, ukázat mu experimenty, vlastnosti těchto látek, které může také sám ověřovat a studovat. Zcela běžně se využívá i nejrůznějších hraček, na kterých lze ukázat využití zákonů fyziky. Jako příklad podobných experimentů budou uvedeny experimenty s gumou a návrh pro využití Kuličkodráhy.
Pružné materiály – polymery – guma
O polymerech a jejich vlastnostech bylo diskutováno již na předešlých konferencích Veletrh nápadů učitelů fyziky (např. R. Holubová 2003, Z. Drozd – Fyzika materiálů – sborník rozšířených příspěvků). Níže uvedeme jednu z dalších možností využití gumy ve výuce fyziky.
Guma má celou řadu vlastností, které jsou zcela jedinečné a mohou být předmětem zkoumání ve fyzice. Zcela běžně jsou prezentovány vlastnosti gumy – její prodloužení na více než pětinásobek, aniž praskne, návrat do původního stavu, aniž bychom zaznamenali deformaci. Tyto vlastnosti má však v dnešní době i řada jiných materiálů. Pružnost gumy je připisována přítomnosti dlouhých řetězců, které mohou vytvářet sítě. Molekuly polymerů či řetězce jsou spojeny chemickými vazbami nebo silnými vodíkovými vazbami. Proces, kdy jsou vytvářeny tyto vazby, je tzv. vulkanizace. Toto síťování zajistí návrat do původního stavu poté, co přestane působit napětí (prodlužování gumy).
V našem případě je zajímavý ten fakt, že pokud je guma prodloužena velmi rychle (adiabaticky), teplota gumy se zvýší.
Pokus 1:
Přiložte gumový pásek ke svým rtům a opakovaně jej rychle natahujte. Rty v našem případě simulují citlivý teploměr. Jsou schopny detekovat nárůst teploty gumy, i když je velmi malý (nenaměřili bychom ani jeden celý stupeň). Tento experiment realizoval již v roce 1806 John Gough.
Obecně změna vnitřní energie dU, která vzniká v důsledku napínání pružného tělesa, může být porovnána s prací dA a teplem, které přijme nebo uvolní těleso podle vztahu dU = δQ –δA. Experimenty ukázaly (Thomson, Joule), že nedochází ke změně vnitřní energie, ale změna teploty je dána prací při prodloužení. Pružnost gumy je určena změnou entropie. Protažení gumy vede k většímu uspořádání polymerních řetězců, entropie klesá (dS je záporné). Při extrémním protažení může dojít ke krystalizaci polymeru, potom se uplatní i změna vnitřní energie.
Příklad pružného míče
Když se uvažuje gumový míč odrážející se od tuhé podložky, dochází k narušení struktury polymeru. Okolí koná práci, která je přeměněna v potenciální energii pružnosti. Pokud vnější síly přestanou působit, molekuly se vrací do původního stavu. Potenciální energie se přemění na práci – míč se odrazí. U ideálně pružného tělesa je práce vnějších sil během deformace úplně přeměněna na potenciální energii pružnosti. U reálného tělesa je část práce přeměněna na teplo. Proto míč nevyskočí do stejné výše, ze které byl vypuštěn.
Na škole se žáci seznamují s délkovou a objemovou roztažností látek a uvádějí si základní vztahy pro výpočet délky či objemu po zahřátí tělesa. Vlivem teploty dochází ke zvětšení objemu látek či jejich prodloužení. Uvádí se anomálie vody. Zajímavé je, že napnutá guma má vlastnosti právě opačné než většina běžných látek – při vyšší teplotě dochází k jejímu zkracování.
Pokus 2
Na stojan zavěsíme gumu a zatížíme ji vhodným závažím. Guma se protáhne na délku l. Poznačíme si délku gumy při protažení za dané teploty ve třídě. Nyní začneme gumu zahřívat, např. pomocí vysoušeče vlasů. Pozorujeme změnu délky gumy. Guma se zkracuje.
Vysvětlení
Gumu délky l0 zatížíme závažím o hmotnosti M. Guma se protáhne na délku l. Koeficient deformace ve směru tahové síly lze vyjádřit vzorcem \( F_{11} = \lambda = \frac{l_0}{l} \).
Příčné zúžení gumy vyjádříme vztahem
\[ F_{22} = F_{33} = \frac{1}{\sqrt{\lambda}} = \sqrt{\frac{l_0}{l}}.\]
Pokud bychom měli tyč, která má rozměry x0, y0, l0, její objem je V0 = x0y0l0 . Pokud zatížíme tyč stejně jako gumu v předchozím případě, tj. hmotností M, lze ukázat, že objem tyče se nezmění.
\[ V = xyz = x_0\sqrt{\frac{l_0}{l}} y_0\sqrt{\frac{l_0}{l}} l_0\frac{l_0}{l} = x_0 y_0 z_0 = V_0 .\]
Chování gumy a tyče lze popsat pomocí změny entropie. Lze ukázat, že závislost S − So na l má maximum pro l = 1, což odpovídá stavu protažení. Entropie nezatíženého stavu je větší než při protažení. Zahřejeme-li gumu – dodáme teplo, dojde ke zvýšení entropie systému. Protažená guma se při zahřátí zkrátí.
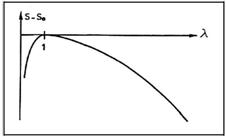
Obr. 1 Závislost S − S0 na λ
Při zatížení se natáhnou molekuly polymeru a změní se jejich síťování. Tahová síla vnáší do systému uspořádanost, tzn. zmenšení entropie. Přísun tepla znamená vždy nárůst entropie. Guma se snaží vrátit do stavu, kdy neuspořádanost byla větší, což odpovídá stavu nenatažené gumy.
Experiment s gumou byl realizován již v roce 1805 Goughem. Guma zatížená závažím se při zahřátí zkrátila, tedy jev opačný než u většiny látek. Při ochlazení se guma opět protáhla, což naznačuje, že proces je vratný. (Gough-Jouleův efekt: http://www.rlhudson.com/O-Ring%20Book/selecting-thermal.html).



Obr. 2 Schéma pokusu – zkrácení gumy
Návaznost na termodynamiku
První věta termodynamiky říká, že změna vnitřní energie může nastat buď přijetím tepla či konáním práce dU = δQ – δA.
Je-li délka l materiálu zvětšena působením tahové síly FT o hodnotu dl, lze práci vloženou do systému vyjádřit jako FTdl. Během pružné deformace dochází ke změně objemu dV a práce pdV je vykonána proti tlaku p. Protože se elastomery (guma) deformují tak, že objem zůstává přibližně konstantní, je práce při změně objemu pdV malá oproti práci, kterou vykoná systém δA = – FT dl. Deformace elastomeru je vratná, proto lze teplo vyjádřit z druhé věty termodynamiky δQ = TdS, kde T je termodynamická teplota, dS je změna entropie systému. Spojením uvedených rovnic lze psát FT dl = dU – T dS. Běžně se všechny experimenty realizují při konstantním tlaku, proto lze pro popis termodynamické rovnováhy použít Gibbsovu volnou energii G = H – TS, pokud deformace nastává při konstancím objemu, je výhodnější použít popis pomocí Helmholtzovy volné energie F = U – TS. Vyjádříme-li změnu Helmoltzovy volné energie při konstantní teplotě, máme dF = dU – TdS. Odtud plyne, že FT dl = dF(T = konst.). Potom
\[ F_T = \left(\frac{\partial F}{\partial l}\right)_T - T\left(\frac{\partial S}{\partial l}\right)_T.\]
První člen odpovídá změně vnitřní energie při napnutí a druhý člen změně entropie. Pro většinu materiálů je důležitý člen odpovídající změně vnitřní energie, u eleastomerů je hlavní změna entropie. Tyto vztahy mohou být zkoumány experimentálně. Podobně lze odůvodnit zahřátí gumy při rychlém napnutí při adiabatickém ději.
Kuličkodráha (Space rail)
Kuličkodráha je stavebnice, kde z jednotlivých komponent je možné sestavovat nejrůznější varianty horské dráhy, včetně zatáček, stoupání, klesání a loopingů. Komponenty tvoří bílá lanka pro sestavení kolejnic, opěrné sloupky, úchyty, výtah, kovové kuličky. Stojany se uchytí do základní desky. Je to pomůcka, která je mimořádně vhodná pro výuku mechaniky a ukázku aplikace zákonů fyziky v praktickém životě a technice. Pro správnou a fungující konstrukci dráhy je třeba aplikovat základní znalosti zákonů mechaniky, o odstředivé síle, dostředivé síle, zákona zachování mechanické energie. Při konstrukci je nutné také volit vhodný rozměr kolejnice, sklon v zatáčkách apod.
Pohyb kovové kuličky je možné sledovat opakovaně, neboť při dojezdu je kulička vyzdvižena výtahem (poháněn baterií) do horní počáteční polohy. Experimentálně je možné ověřit např. řešení úlohy typu: Jaká musí být počáteční výška H horské dráhy, má-li vozík bezpečně projet vertikálním kruhovým obloukem o poloměru R? Valivý odpor kol a odpor vzduchu zanedbejte. Vozík považujte za hmotný bod. U kuličkodráhy je vozík nahrazen kovovou kuličkou. Je dále možné danou kuličku, která je součástí stavebnice, nahradit kuličkami vlastními, z různých materiálů a různé hmotnosti. Pokud volíme kuličku větší, objeví se jedině problém s výtahem, jehož rozměry jsou dimenzovány na dodávané příslušenství.

Obr. 3 Kuličkodráha v laboratoři KEF
Literatura
[1] Geethamma, V. G., Thomas, S.: Why Does a Rubber Ball Bounce? In: Resonance, April 1997, str. 48-54.
[2] I'Anson, S.: Thermodynamics of Rubber Elasticity. [on-line 1.9.2011: personal pages.manchester.ac.uk/.../rubber.../Thermodynamics_of_Rubber_]