Nie je váženie ako váženie
Ľubomír Machovič, Ivan Baník
Abstract
The paper is dealt with exotic manners of weighing, which facilitate the development of physical notion. They can be used, among other, for the determination of mass density in house conditions.
Úvod
Určenie hmotnosti nejakého bežného predmetu bez osobitných technických pomôcok, ako sú váhy, je vhodným námetom na fyzikálne uvažovanie a pestovanie tvorivého myslenia pokiaľ ide o výber jednak metódy či použitých prostriedkov.
Pokusy pre najmenších
Problém je aktuálny už aj v prípade tých najmenších školákov, kedy sa najvhodnejšie javí váženie pomocou pravítka a mincí. Pravítko použijeme ako dvojramennú páku podloženú ceruzou s kruhovým prierezom pod jej ťažiskom. Ak zadáme hodnotu hmotnosti mince, môžeme určiť hmotnosť gumy na gumovanie, hmotnosť patentného kľúča, orezávača ceruziek a pod. Tak možno určiť aj hmotnosť ľahkej pórovitej špongie na umývanie riadu a na základe toho, po zmeraní rozmerov špongie, aj jej hustotu. Podobne možno určiť hustotu gumy. Nám dospelým je, ak sa pozrieme na stav vyváženia dvoch rôznych drobnejších predmetov na dvojramennej páke, jasné, že kratšie rameno sily prislúcha ťažšiemu predmetu, no deťom to jasné byť nemusí. Skúsenosti sa získavajú v živote postupne. Objasní sa to napríklad aj pokusom, ak namiesto jednej mince na jednej strany páky dáme dve rovnaké na seba, no na druhej strane zostane iba jedna pôvodná rovnaká minca.
Pomocou známej hmotnosti mince môže dieťa za pomoci rodičov určiť aj hmotnosť pravítka. Pravítko s mincou na ňom vysúva za okraj stola, až dosiahne kritický stav, pri ktorom by sa už sústava prevrátila okolo hrany stola. Z podmienky rovnováhy (momentov síl) určí hmotnosť pravítka, uvedomujúc si pritom úlohu ťažiska pravítka ako pôsobiska tiaže pravítka. Pomocou pravítka teraz už známej hmotnosti vieme určovať hmotnosť iných predmetov. Tak sa dajú verifikovať aj výsledky iných predtým vykonaných meraní.
Váženie metódou sústavy dvoch rovníc
Váženie podobného druhu ako s pravítkom sa dá realizovať aj v doskovej obmene. Ako závažie známej hmotnosti je vhodná tabuľka čokolády, hmotnosť ktorej býva uvedená na jej obale. Poučným a zaujímavým námetom v súvislosti s vážením pomocou dosky je toto váženie znázornené na obr. 1.
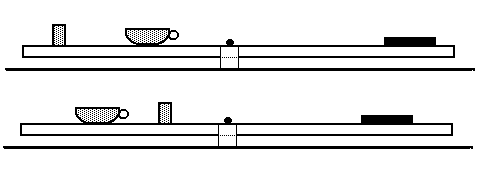
Obr. 1
Na doske, otáčavo uloženej pomocou ceruzy a držanej o dosku gumičkami do vlasov, nad jej ťažiskom rozložíme tri telesá a sústavu vyvážime. Hmotnosti dvoch telies nepoznáme, avšak hmotnosť jedného z nich (tabuľky .čokolády) je známa. V zobrazenom prípade sú to šálka na kávu a pohárik. Sústavu pomocou tabuľky čokolády vyvážime. Úlohou je určiť hmotnosti daných dvoch telies. Zobrazený stav poskytuje však len jednu lineárnu rovnicu o dvoch neznámych hmotnostiach. Určenie oboch hmotností sa dá dosiahnuť len na základe údajov zistených v dvoch rôznych situáciách rovnováhy, čím sa získa sústava dvoch rovníc o dvoch neznámych. Analýza problému je veľmi poučná a názorná. Obvyklé x a y znamenajú dve neznáme hmotnosti a príslušné koeficienty znamenajú ramená príslušných tiaží. Na druhej strane rovnice vystupuje hodnota určená zo známej hmotnosti čokolády a príslušného ramena jej tiaže. V druhej rovnici vystupujú tie isté neznáme, no koeficienty budú všeobecne iné a iná bude aj hodnota pravej strany. Sústavu možno obvykle riešiť a zistiť tak neznáme dve hmotnosti. No existujú aj výnimky, čo sa tu práve názorne dá objasniť. Keby boli všetky ramená síl v druhej situácii napr. polovičné ako v prvej, získané dve rovnice by neboli nezávislé a riešenie by nebolo jednoznačné. Na druhej strane, keby sme vytvorili sústavu dvoch rovníc tak, že by ľavé strany oboch boli rovnaké a na pravej strane druhej napísali mylný údaj, sústava by nemala riešenie. Tieto úvahy s rovnováhou môžu prispieť k hlbšiemu chápaniu príslušného matematického problému spätému so sústavou. V zásade by sa dalo uvažovať podobne aj o vážení troch predmetov.
Impulzná metóda váženia
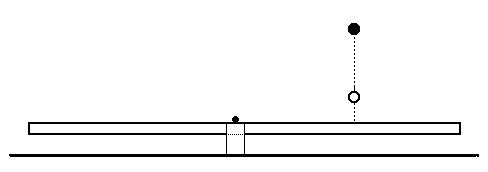
Obr. 2
Na obr. 2 je znázornená podstata „impulznej“ metódy váženia guľôčky, ktorú z určitej výšky pustíme na dosku nachádzajúcu sa v rovnováhe. Guľôčka sa od dosky odrazí do určitej menšej výšky, ktorú odhadneme. Z oboch zaregistrovaných výšok vieme určiť zmenu rýchlosti guľôčky pri odraze. S touto zmenou súvisí však aj zmena hybnosti guľôčky pri odraze. Z hľadiska nášho zámeru je však dôležitá zmena momentu hybnosti guľôčky vzhľadom na os rotácie podoprenej dosky. Sústavu považujeme za izolovanú, takže zmena momentu hybnosti guľôčky, ktorú po odraze chytíme musí byť rovnaká ako zmena momentu hybnosti dosky, ktorá sa po náraze rozkmitá ako fyzikálne kyvadlo. Z amplitúdy jej kmitov, ktoré prebiehajú po náraze vieme určiť štartovaciu uhlovú rýchlosť dosky po náraze a pri známej hmotnosti dosky a pri známom momente zotrvačnosti dosky aj jej moment hybnosti. Zo zákona zachovania momentu hybnosti dostaneme nakoniec vzťah, z ktorého sa dá určiť neznáma hmotnosť guľôčky. Pri uvedenej metóde nejde ani tak o samotné váženie, ako skôr o hľadanie zaujímavých fyzikálnych súvislostí, čím sa precvičuje učivo mechaniky na vysokej škole.
Určovanie hustoty
Na obr. 3 je zobrazené meranie hustoty feritov metódou váženia feritov na vzduchu a vo vode. Na váženie využívame pravítko, ktorého hmotnosť bola určená už predtým. V obidvoch prípadoch dáme pravítko do kritickej polohy, kedy by sa už preklopilo na hrane stola a zmeriame ramená síl. Kritická poloha pravítka je pre obe situácie odlišná, čo nám poskytne podklady pre určenie hustoty feritov. Podobným spôsobom možno určiť hustotu porcelánu šálky na kávu s využitím dosky.
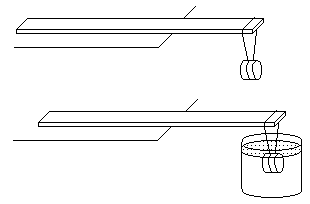
Obr. 3
Nitkové váhy
Iný spôsob váženia je znázornený na obr. 4, kde ide o tzv. nitkové váhy. Tie sa realizujú tentoraz na okraji stola pomocou dvoch kníh a nití. Na jednej zvislej niti je zavesená tabuľka čokolády a na druhej vážený predmet. Niť medzi oboma predmetmi má byť napnutá a vodorovná. Knihy možno po stole vhodne premiestňovať. Analýza problému je pre žiakov i študentov podnetná.
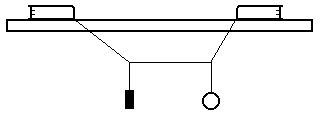
Obr. 4
Váženie pomocou podtlaku
Zvláštne a tak trochu exotické váženie misky je znázornené na obr. 5. Misku pri ňom držíme zdvihnutú pomocou lievika obráteného širokým otvorom nadol. V lieviku vytvárame ústami pomocou hadičky podtlak, ktorý meriame pomocou ďalšej hadičky. Ak zaznamenáme kritickú výšku vody, pri ktorej miska od lievika odpadne a tiež plochu kruhového otvoru lievika, ktorou sa lievik dotýka misky, vieme z týchto údajov určiť hmotnosť misky. Ide o orientačné meranie a vlastne skôr o zamyslenie sa nad ním.
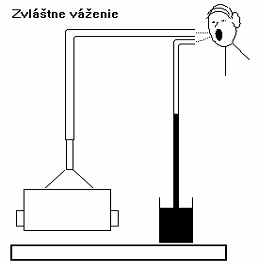
Obr. 5
Váženie s využitím vztlakovej sily
Poučné je aj váženie znázornené na obr. 6. Pri ňom je na váhach položená nádobka s vodou, do ktorej rukou ponárame prázdnu plastovú fľašu. Pozorujeme pritom zmenu údaja váh. Čím je hlbší ponor fľaše, tým väčší je údaj váh. Ide tu samozrejme o reakciu na vztlakovú silu pôsobiacu na ponárané teleso. Vztlaková sila rastie so zväčšovaním objemu ponorenej časti fľaše, čím narastá aj príslušná reakcia.
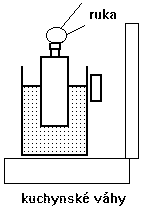
Obr. 6
Váženie pomocou dosky
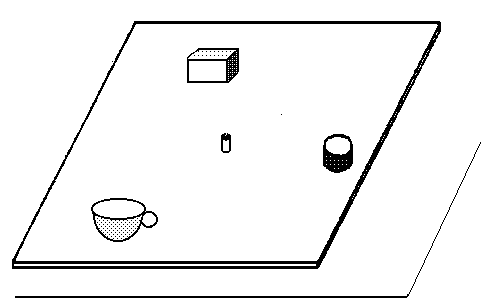
Obr. 7
Váženie dvoch predmetov súčasne pomocou dosky je znázornené na obr. 7. Pri ňom sa využíva doska podoprená pod ťažiskom. Na doske sú položené dva predmety neznámych hmotností. Dosku vyvážime pomocou telesa známej hmotnosti. Z podmienky rovnováhy dostaneme všeobecne dve rovnice: jedna plynie z podmienky rovnováhy vzhľadom na jednu os prechádzajúcu bodom podoprenia, druhá pre inú os, napríklad pre os kolmú na prvú. V špeciálnom prípade, ak by všetky tri predmety ležali na jednej priamke prechádzajúcej bodom podoprenia, by sme dve hmotnosti naraz určiť nemohli.
Váženie s tabuľkou čokolády
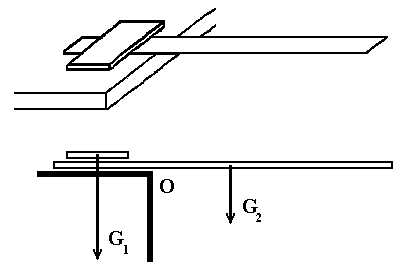
Obr. 8
Iná zostava pre váženie, vhodná pre tých menších, je znázornená na obr. 8. Pri nej využívame tabuľku čokolády ako teleso známej hmotnosti. Meraním sa zistí hmotnosť pravítka, resp. doštičky. Rozloženie pôsobiacich síl vystihuje dolná časť obrázku.
Literatúra
[1] BANÍK I., BANÍK R.: Fyzika netradične - Mechanika, Alfa, Bratislava, 1990.
[2] BANÍK I., BANÍK R.: Kaleidoskop učiteľa fyziky 1-10, MC Bratislava, 1992-2000.
