Několik nápadů nejen z kroužků fyziky

Miroslav Jílek

Abstract

This paper describes several ideas from a program of practical seminar for high school students interested in Physics, which is organized at MFF UK in Prague. The ideas and experiments described here can be used in Physics lessons and seminars or for experimenting by anyone who is motivated.

Úvod

V příspěvku popisuji stručně několik námětů na experimentální práci se studenty v hodinách fyziky a různých fyzikálních seminářích. Většina uváděných námětů vychází z činnosti kroužků fyziky, které byly letos třetím rokem pořádány pro středoškolské studenty na KDF MFF UK v Praze. Program kroužků s fotodokumentací a podrobnějším popisem většího množství experimentů, které si studenti měli možnost vyzkoušet a blíže prozkoumat, se připravuje v elektronické formě pro prezentaci na internetu. Na web-stránkách [1] je zatím možné shlédnout studijní materiál týkající se srážek a rotací těles, který byl zpracován na základě části programu starších ročníků kroužků fyziky.

Fyzika s digitálním fotoaparátem

Digitální fotoaparát se stává stále více rozšířeným a dostupným zařízením, které může především ve spojení s počítačem, eventuelně s datovým projektorem, účinně sloužit jako pomůcka ve výuce fyziky i k vlastnímu zkoumání okolního světa. Způsobů využití digitálního fotoaparátu je jistě celá řada a na tomto místě uvádím pouze několik vyzkoušených možností vhodných pro další rozvíjení a zdokonalování.

Makrofotografie

Jedním z nejjednodušších způsobů využití digitálního fotoaparátu je pořizování detailních záběrů malých objektů. Toho lze využít například pro měření povrchového napětí vody. Injekční stříkačkou se silnější jehlou nebo tenkou kapilárou odkapáváme pomalu kapičky vody v těsné blízkosti pravítka s milimetrovou stupnicí. Těsně před odkápnutím se snažíme kapičky vyfotit proti pravítku z nejbližší možné vzdálenosti. Zvětšenou fotografii si prohlédneme na obrazovce fotoaparátu nebo lépe na počítači a můžeme tak poměrně přesně odhadnout velikost kapky i průměr protaženého „krčku“ kapky před odkápnutím. Z velikosti kapky a obvodu „krčku“ určíme známou metodou, viz například Určení povrchového napětí kapaliny kapkovou metodou v [2], povrchové napětí vody. Výhoda této metody spočívá především v možnosti pozorování reálného tvaru kapky během odkapávání.

Prohlížení makrofotografie zvětšené na počítači můžeme použít také pro zkoumání zdánlivě hladkých povrchů například papíru, kancelářské sponky, zápalky… a diskutovat například vznik třecí síly na těchto površích. Drobné předměty a povrchy můžeme samozřejmě dále fotografovat i pomocí lupy nebo mikroskopu, přičemž výsledek vidíme a můžeme upravovat mnohem rychleji než v případě klasické fotografie.

Zkoumání vrhů těles

Většina digitálních fotoaparátů umožňuje nahrávání krátkých videoklipů s rychlostí snímkování například 15 snímků za sekundu. Pomocí této funkce lze snadno zkoumat nejrůznější dynamické procesy. Výhodou oproti klasickému videu je jednodušší manipulace s nahraným videoklipem, který není příliš velký, a je možné ho okamžitě přehrát snímek po snímku na počítači nebo v samotném fotoaparátu.

Jako příklad může sloužit zkoumání trajektorií vrhů těles. Libovolný malý míček nebo jiný drobný předmět hodíme nebo vystřelíme pomocí jednoduchého praku před větší popsanou tabulí a zdálky tento vrh zaznamenáme jako video pomocí fotoaparátu. Následným přehráváním videoklipu snímek po snímku sledujeme polohy míčku v jednotlivých časových úsecích (např. patnáctinách sekundy) a tyto polohy zaznamenáváme na tabuli, což umožní zakreslit reálnou trajektorii vrhu (popsaná tabule usnadní určování poloh, na čistou tabuli lze dopředu narýsovat jednoduchou souřadnicovou síť). Ze vzdáleností uražených míčkem za příslušné časové okamžiky můžeme určovat průměrnou rychlost míčku v jednotlivých úsecích nebo můžeme z naměřenou trajektorií libovolně dále pracovat.

Stejným způsobem lze zkoumat také volný pád, pád většího lehkého předmětu (papírové koule, krabičky z pěnového polystyrenu…) v odporovém prostředí a nejrůznější jiné druhy pohybů.

Prostorové fotografie a videa

Zajímavou metodou přiblížení principu prostorového vnímání lidského zraku může být tvorba vlastních prostorových fotografií, které někdy bývají k vidění ve speciálních publikacích. K prohlížení těchto fotografií jsou potřeba brýle tvořené dvěma (pro každé oko jedním) barevnými filtry (foliemi nebo skly) například červeným a zeleným. Takové brýle bývají součástí zmiňovaných publikací, nebo je lze nahradit libovolnými filtry pro demonstraci skládání barev, eventuelně použít barevné foliové filtry pro osvětlovací reflektory.

Pro fotografii vybereme dostatečně „prostorový“ objekt – například členitou místnost s různými předměty a osobami. Objekt vyfotíme ze stativu, fotoaparát posuneme rovnoběžně asi deset centimetrů stranou a vyfotíme stejný objekt ještě jednou (focené osoby by se mezi pořízením obou snímků neměli příliš pohybovat). Získáme tak dva mírně posunuté snímky, které je nutné zpracovat na počítači. Oba snímky (levý a pravý) převedeme v programu pro zpracování fotografií do stupňů šedé a vytvoříme si ještě jeden prázdný (černý) obrázek stejné velikosti jako fotografie. Pomocí funkce sloučit kanály všechny tři obrázky sloučíme, přičemž jeden (levý) snímek označíme jako červený kanál – R, druhý (pravý) snímek označíme jako zelený kanál – G a zbývající prázdný snímek označíme jako modrý kanál – B. Získáme tak červenozelenou fotografii, která pozorována červenozelenými brýlemi vytvoří prostorový obraz foceného objektu. Informace o prostorovém uspořádání je dána tím, že fotografie obsahuje dva překryté obrazy stejného objektu, focené z poněkud jiného úhlu. Při prohlížení odfiltrují brýle pro každé oko vždy jeden obraz, takže situace je obdobná pozorování objektu oběma očima, kdy také každé oko vidí objekt z poněkud jiného úhlu.

Pokud máme k dispozici dva stejné digitální fotoaparáty, můžeme se pokusit vytvořit dokonce prostorové video. Oba fotoaparáty připevníme těsně vedle sebe například k dřevěné liště tak, aby jejich objektivy směřovaly rovnoběžně. Na obou fotoaparátech spustíme současně nahrávání videa a pořídíme tak dva krátké videoklipy, každý snímaný z poněkud jiného úhlu. Další zpracování už je obdobné vytváření prostorové fotografie, jenom je zdlouhavější. Snímek po snímku musíme oba klipy sloučit a z takto vytvořených snímků zpětně složit celou animaci. Počet skládaných snímků samozřejmě závisí na délce pořizovaného videa. Pro tento proces si „počítačově zdatní“ zájemci mohou samozřejmě vytvořit také krátký program.

Prostorové fotografie i videa si lze prohlížet buď přímo na monitoru počítače nebo, což je efektnější, promítaná (v setmělé místnosti) pomocí projektoru. Podobného principu využívají také prostorová kina typu IMAX, kde jsou ale místo dvou barevných obrazů současně promítány dva (posunuté) příčně polarizované obrazy, které se prohlížejí pomocí brýlí s příčně polarizovanými skly.

Zrcátkový dálkoměr

Jednoduché zařízení pro měření vzdáleností lze vyrobit ze dvou latí – například 1 m dlouhých, zrcátka a sklíčka (například podložního sklíčka k mikroskopu). Latě spojíme na jednom konci hřebíkem nebo šroubem, který slouží jako čep, kolem kterého se mohou latě otáčet. Ke spodní lati připevníme těsně za čep pomocí dřevěného hranolku zrcátko tak, aby svíralo s latí úhel 45°. Sklíčko z jedné strany začadíme v plameni svíčky (některá místa mohou být začazena více, některá méně) a vytvoříme tak polopropustné zrcátko, které odráží nezačazenou plochou. Sklíčko umístíme opět pomocí malého dřevěného hranolku na opačný konec horní latě, než je čep, okolo kterého se otáčí. Vzniklý dálkoměr je tedy tvořen dvěma rovnoběžnými zrcátky (jedním polopropustným) umístěnými (šikmo k latím) na vzdálenost latě od sebe. Při mírném pootáčení latí vůči sobě se mírně mění úhel mezi zrcátky.

Měření pomocí dálkoměru provádíme tak, že držíme spojené latě vodorovně před sebou (jako příčnou flétnu) a díváme se na vzdálený objekt skrz polopropustné sklíčko. Odrazem od sklíčka zároveň vidíme obraz objektu z druhého (bočního) zrcátka. Mírným posouváním volných konců latě vůči sobě se nám oba obrazy posouvají vůči sobě a při jejich překrytí zaznamenáme úhel, který svírají latě a tedy i zrcátka. Měřený úhel je velmi malý, proto si předem na konec jedné latě nakreslíme část úhloměrné stupnice se středem v ose otáčení latí. Tuto stupnici můžeme pro přesnější odčítání vybavit jednoduchým noniem.

Před měřením vzdáleností je třeba srovnat zrcátka, aby byla přesně rovnoběžná při nulovém úhlu mezi latěmi. To uděláme tak, že pozorujeme hodně vzdálený objekt (nejlépe Slunce za mraky nebo při západu) a při překrytí obrazů si označíme nulový úhel.

Vzdálenost pozorovaného objektu určíme jednoduše z pravoúhlého trojúhelníka jehož kratší odvěsnu tvoří spojnice mezi zrcátky, druhou odvěsnu představuje paprsek přicházející z měřeného objektu do oka skrz polopropustné sklíčko, přeponu představuje paprsek přicházející z objektu do bočního zrcátka. Úhel mezi přicházejícími paprsky (v Astronomii nazývaný paralaxa) je díky zákonu odrazu dvojnásobkem úhlu sevřeného zrcátky. K určení vzdálenosti tedy stačí znát vzdálenost mezi zrcátky a úhel, který svírají.

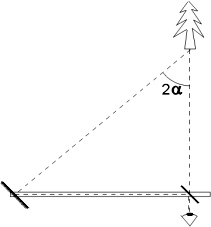
Přesnost měření vzdáleností záleží především na přesnosti určení úhlu mezi zrcátky. Při vzdálenostech kolem 100 m lze dosáhnout odchylky menší než 0,5 m.

Obdobný princip měření vzdáleností se kromě astronomických měření vzdáleností využívá například u dálkoměrů v některých starších typech fotoaparátů nebo u velkých dálkoměrů umístěných na námořních bitevních lodích.

Ještě jednodušší podobný model přibližující funkci dálkoměru tvořený dvěma obyčejnými zrcátky demonstroval doc. L. Dvořák na jednom ze starších ročníků seminářů pro budoucí učitele fyziky na Malé Hraštici, viz [3].

Louskáček na ořechy

Jak velká síla je potřebná k rozlousknutí vlašského ořechu? Louskáček sestrojený podle námětu v [4] to umožňuje změřit.

Louskáček je tvořen dřevěným rámem asi 50 cm dlouhým a 10 cm vysokým k jehož kratší straně dosedá dřevěný hranolek otočný na jednom konci kolem šroubu, který je pomocí dvou kovových pásků spojen s rámem. Mezi volný konec otočného hranolku a horní část rámu se vkládá ořech. Podél horní dlouhé strany rámu je potom napnuté pevné ocelové lanko, které je na jednom konci přišroubováno zboku k rámu, na druhém konci prochází těsně nad ořechem otvorem v otočném hranolku a je ukončeno uzlem za kovovou podložkou. Napnutí lana je zajištěno dřevěným klínkem s podélnou drážkou, který se vkládá mezi podložku a otočný hranolek.

Po vložení ořechu do louskáčku a dopnutí lanka podržíme jednou rukou pevně dřevěný rám a druhou rukou zatáhneme za lanko v jeho středu směrem nahoru. Síla, která přitom k sobě svírá rám s otočným hranolkem a způsobuje rozlousknutí ořechu je mnohem větší než síla, kterou působíme na lanko.

Velikost síly F1, kterou působíme na lanko můžeme měřit pomocí siloměru nebo mincíře. Pokud zároveň změříme pravítkem výšku d do které natáhneme lanko nad rám a délku rámu L, můžeme z podobnosti trojúhelníku tvořeného rámem s drátem a trojúhelníku daného působícími silami určit jednoduše velikost síly F2 působící na ořech jako:

Je zajímavé, že pevnost vlašského ořechu velmi závisí na směru, kterým se ho snažíme rozlousknout. Nejpevnější je, působíme-li silami kolmo na rovinu danou spojením obou polovin skořápky. Síla napínající lanko může být v takovém případě tak velká, že dojde k jeho přetržení.

Velikost síly potřebné k rozlousknutí ořechu lze také ověřit pomocí osobní váhy, na kterou položíme dřevěné prkénko s ořechem a přikryjeme druhým prkénkem. Horní prkénko potom postupně zatěžujeme nohou, dokud ořech nepraskne. Hmotnost, kterou ukazuje váha těsně před prasknutím ořechu určuje tíhu způsobující rozlousknutí ořechu.

Závěr

Některé další nápady realizované na kroužcích fyziky pro středoškolské studenty jsou popsány a v elektronické podobě přístupné na internetu, například co vše se dá zjistit z ohýbání obyčejných špejlí,viz [5].

Jiné realizované náměty jako pokusy s mikrovlnkou, lupy a mikroskopy z kapky vody, dírkové a štěrbinové (zkreslující) komory, zkoumání tepelné vodivosti a vyzařování látek a další jsou spolu s podrobnějším popisem námětů uváděných v tomto příspěvku připravovány pro umístění na webu.

Literatura

[1] JÍLEK, M. Srážky a rotace, http://fyzweb.cuni.cz/dilna/krouzek/uvod.htm

[2] BARTUŠKA, K., SVOBODA, E. Fyzika pro gymnázia - Molekulová fyzika a termika, PROMETHEUS Praha 2000

[3] DVOŘÁK, L. Jarní soustředění pro posluchače učitelství fyziky a „spřízněné duše“ na Malé Hraštici, http://kdf.mff.cuni.cz/Hrastice/index.htm

[4] DOWNIE, N. A. Vacuum bazookas, electric rainbow jelly, and 27 other Saturday science projects, Princeton University Press Princeton 2001

[5] JÍLEK, M. Ohýbání špejlí, http://fyzweb.cuni.cz/dilna/spejle/spejle.htm