Několik pokusů k pochopení pojmů tlak a tlaková síla

Jan Dirlbeck

Pomocí několika pokusů se snažím žákům objasnit pojmy tlak a tlaková síla. Žáci velmi rychle přijmou tvrzení učitele, že tlak se vypočítá, vydělíme-li tlakovou sílu plochou. Zejména pokud použijí kalkulačky, naučí se velmi rychle a úspěšně pracovat se vzorcem:

p = F/S

Takovéto úlohy snadno vypočítají. Problém nastane, mají-li vysvětlit rozdíl mezi pojmem tlak a tlaková síla. Velmi často jim oba pojmy splývají. Proto jsem sestavil několik pokusů s následnými aplikacemi v praktickém životě, na nichž se snažím oba pojmy nejen vysvětlit, ale především je přesněji vymezit.

První pokus provádím s kvádrem (používám olověný), barevným gelem v sáčku a zpětným projektorem. Na sáček s gelem, který je prosvícen, položím hranol největší plochou. Kvádr část gelu vytlačí a v daném místě je vidět zesvětlení gelu. Potom položím kvádr menší plochou na sáček, gel je kvádrem prakticky vytlačen a intenzita procházejícího světla je větší. Uděláme závěr, že při stejné hmotnosti a tedy tlakové síle, se změnil tlak, kterým působí kvádr na gel. Že můžeme velikost tlaku ovlivnit velikostí plochy, prokážeme položením kvádru na gel nejmenší plochou. V tomto případě je gel vytlačen do stran a meotar prosvítí bílou stopu po ploše kvádru. Tak většina žáků pochopí rozdíl mezi tlakovou silou, která je v tomto případě stále stejná, a tlakem, který závisí na ploše, na niž těleso působí.

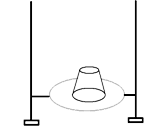
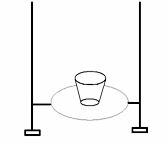
Na příkladech z praxe formou otázek řešíme pojem tlak a tlaková síla. Proč nákladní automobily mají více a širší kola v zadní části? Proč traktory mají zadní kola širší? Proč při válení těsta používáme váleček? Proč se tenký led na rybníku prolomí snadněji pod bruslařem? Protože, ale žáci dnes znají spíše umělá kluziště, předvedu další pokus. Použiji kulatý rámeček na vyšívání a komolý jehlan. Do rámečku napnu fólii ze sáčku do odpadkových košů.

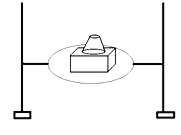
Vložím-li jehlan větší podstavou na fólii, která představuje „ledový škraloup“, fólie tlak jehlanu vydrží. Změním-li podmínky tak, že položím jehlan na fólii menší plochou, jehlan fólii protrhne. Opět uděláme závěr, že při stejné hmotnosti, ale jiné ploše se tlak zvětšil a to natolik, že došlo k destrukci podložky. Odtud odvodíme správné chování na ledové ploše, dojde-li k jejímu prolomení a pokusu o záchranu postiženého. Abychom ukázali, že tlak závisí také na tlakové síle, pokus pozměníme takto. Na silnější fólii položíme těleso. Protože tvrdíme, že velikost tlaku závisí také na tlakové síle, zvětšíme ji položením dalšího tělesa na prvé těleso. Zvětšila se hmotnost, tedy se zvětšila i tlaková síla a dojde k protržení fólie.

A opět ze života uvedeme příklady, které s tímto pokusem souvisejí. Například přetěžování kamiónů na silnicích a následně vymačkávání kolejí do vozovky. Velká hmotnost lokomotivy umožňující pohyb po hladkých kolejích. V domácnosti použití lisu na česnek, otvíráků na konzervy,…

Dalším pokusem se můžeme zaměřit na zjevný rozdíl tlaku, který působí na podložku, nebo na závěs. Stejné těleso např. opět kvádr vložíme žákovi na nastavenou dlaň, a poté ho necháme stejné těleso držet na závěsu z provazu. Žák dojde k závěru, že těleso na závěsu je těžší. Při stejné síle ( hmotnosti tělesa ) tedy rozpozná různé účinky na ruku. Obměna tohoto pokusu spočívá ve dvou stejně hmotných tělesech, která vložíme na otevřené dlaně žáka. Působí stejná síla. Působí-li na stejnou plochu, žák prohlásí, že tělesa jsou stejná. Pokud změníme velikost plochy u jednoho tělesa jeho překlopením, žák oznámí, že toto těleso je lehčí – působí menší silou. Tyto pokusy je vhodné provést s jedním žákem a to ještě s úpravou – žákovi zavážeme oči. Opět můžeme navázat na zkušenosti ze života a to ucha u nákupní tašky, popruhy u batohů apod.

K poslednímu pokusu se dá využít auto ze stavebnice Merkur a modelína, nebo těsto na vizovické pečivo. Žákům připravíme plochu pokrytou modelínou nebo těstem a dáme jim autíčko s koly zbavenými pneumatik. Po přejetí takto upravené podložky se v podložce objeví rýhy po ráfcích. Obujeme-li pneumatiky a znovu autíčkem přejedeme po podložce stopy budou méně zřetelné nebo téměř nezřetelné. Opět zde tlak závisí na velikosti styčných ploch. Odvodíme, proč v druhém případě se auto do podložky tolik neboří? A zase navážeme na zkušenost se sněhem a botou bez lyže a opatřenou lyží.

V poslední kroku vybíráme příklady z praxe kolem nás a snažíme se najít souvislost mezi tlakem, tlakovou sílou a plochou. Rozebíráme, jak případně ovlivnit výsledek, aby vyhovoval našim záměrům.

Tedy:

• Auto se propadá v písku. Řešení: Podhustit pneumatiky – tedy zvětšit styčnou plochu.

• Ostrý nůž řeže lépe. Řešení: Malá styčná plocha – tedy možnost působení menší tlakové síly.

• Tenká injekční jehla způsobuje menší bolesti. Řešení: Malá plocha - působení menší síly.

• Terénní vozidla v měkkém terénu. Řešení: Zvětšit plochu pomocí pásů.

• Zapichování špendlíků, jehel. Řešení: Zvětšit plochu - větší hlavičky, použití náprstku.

• Přechod rohožky v lodičkách. Řešení: Přenesení síly na špičku boty - větší plocha.