Netradiční měřící přístroje 4: měření krátkých časů

Leoš Dvořák

Abstract

A simple device for measuring of short time intervals using charging of a capacitor is described. At schools it can be used to motivate the investigation of behaviour of RC circuits. Time intervals which can be measured range since tens of microseconds or less to at least seconds. As an example a measurement of a time of a collision of a hammer hitting an anvil is described.

Úvod

Tento příspěvek navazuje na sérii příspěvků s analogickými názvy (viz např. [1]) prezentovaných na minulých ročnících „Veletrhu nápadů“. I v tomto případě jde o námět na experiment resp. sérii experimentů využitelných ve výuce fyziky na SŠ – a s případnými zájemci např. v rámci kroužku fyziky již od ZŠ. Základní experiment byl vyzkoušen na Jarním soustředění pro posluchače učitelství fyziky na Malé Hraštici (viz [2]) v květnu 2004.

Motivace: úder kladiva na kovadlinu

Udeříme-li kladivem na kovadlinu, odrazí se. Chvíli ovšem byly kladivo a kovadlina v kontaktu. Jak dlouho ten kontakt trval? Jinými slovy: jak dlouho trval úder?

Podobný problém můžete žákům a studentům předložit buď přímo nebo v rámci mechaniky v partiích zabývajících se souvislostí síly a časové změny hybnosti. Známe-li totiž hybnost kladiva před dopadem a předpokládáme-li, že jde o pružný ráz a kovadlina je výrazně hmotnější než kladivo, je charakteristická velikost síly úderu rovna F = Δp / Δt = 2p / Δt, kde Δt je doba trvání úderu.

Sledujeme-li kladivo a kovadlinu, může se nám doba úderu zdát „nezměřitelně malá“. Mladší generace žáků a studentů ovšem asi nebude překvapena, že ji lze změřit pomocí počítače, například systémem ISES. (Šlo by též využít zvukové karty a vhodného programu.) Spojíme-li jednu svorku měřicí karty s kovadlinou a druhou přes baterii a rezistor s kladivem, teče při dotyku kladiva a kovadliny proud. Průběh proudu lze na počítači zobrazit a odečíst, jak dlouho dotek trval. Takto se daný experiment již léta provádí v přednáškách z mechaniky pro 1. ročník na MFF UK.

Šlo by to i bez počítače? Uvidíme, že ano. Dokonce tak můžeme měřit i výrazně kratší časy, s nimiž by některé počítačové měřicí systémy už mohly mít potíže. Navíc náš experiment bude pěknou motivací pro zkoumání vlastností kondenzátoru, resp. kombinace RC. Vlastně celé naše zařízení nebude ani žádný „měřicí přístroj“, ale několik součástek, které lehce propojíme dohromady – a nevyjdou nás na víc než pár korun.

Jednoduché měření – a něco málo výpočtů pro středně pokročilé

Naše měření využije nabíjení kondenzátoru. Na počátku měření je kondenzátor vybit. Svorky A a B jsou spojeny s kladivem a kovadlinou. Při doteku kladiva a kovadliny se kondenzátor přes rezistor R začne nabíjet. Z výsledného napětí na kondenzátoru můžeme určit, jak dlouho byly svorky spojeny.

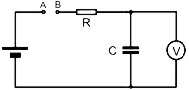
Celý proces samozřejmě můžeme popsat teoreticky – stačí si vzpomenout, cože jsme to slýchali někde v prvním ročníku vysoké školy. Označíme-li napětí baterie U_b a napětí na kondenzátoru U, teče do kondenzátoru proud I = (U_b-U)/R. (Proud tekoucí voltmetrem zanedbáme.) Za čas Δt přiteče do kondenzátoru náboj ΔQ = I·Δt, takže se napětí na něm zvětší o ΔU = ΔQ / C = (U_b-U)·Δt / R·C), z čehož po vydělení Δt a limitě Δt→0 dostaneme krásnou diferenciální rovnici dU/dt = (U_b-U)/(R·C), jejíž řešení pro danou počáteční podmínku je U = U_b·(1-exp(-t/T)), kde časová konstanta T=RC. Odtud t = –T · ln(1–U/U_b).

Takhle se dá vztah mezi časem t a napětím U popsat na úvodní vysokoškolské úrovni. S podrobnějším komentářem lze podobné odvození prezentovat i vážnějším zájemcům z řad středoškoláků např. na kroužku fyziky, zejména pokud jim chceme ukázat, jak šikovnou věcí jsou pro fyziku diferenciální rovnice. Pro „normální lidi“ se naštěstí obejdeme i bez nich.

Jak to spočítat zcela jednoduše

Výpočet času se výrazně zjednoduší, pokud je napětí U na kondenzátoru podstatně menší než napětí baterie. Pak je proud I tekoucí do kondenzátoru prakticky konstantní. Náboj kondenzátoru, a tedy i napětí na něm, proto roste přímo úměrně s časem.

Jednoduše lze vše vysvětlit na konkrétním případě, kdy kondenzátor budeme nabíjet z ploché baterie o napětí U_b = 4,5 V přes rezistor o odporu R = 4,7 kΩ. Do kondenzátoru pak teče proud přibližně 1 mA. Za 1 milisekundu přiteče do kondenzátoru náboj asi 1 mikrocoulomb. (ΔQ = I·Δt = 10^-3A·10^-3s = 10^-6C)

Má-li kondenzátor kapacitu C = 100 μF = 10^-4F, stoupne na něm za uvedenou 1 ms napětí o 1μC/100μF = (1/100) V, tj. o 10 mV. (ΔU = ΔQ / C = 10^-6C/10^-4F = 10^-2V). Jedné milisekundě proto odpovídá 10 milivolt, desetině milisekundy 1 milivolt.

S danými hodnotami součástek tedy stačí naměřené napětí v milivoltech dělit deseti a dostaneme čas v milisekundách. Spokojíme-li se s přesností řádu procent, můžeme takto měřit časy do desítek milisekund. Porovnání s přesným vzorcem odvozeným výše ukáže, že ještě pro 40 ms činí chyba méně než 5%.

Vnitřní odpor voltmetru a další vlivy

Až dosud jsme považovali vnitřní odpor voltmetru za nekonečný. V reálném zapojení se kondenzátor bude přes vnitřní odpor voltmetru RV vybíjet. Jak to ovlivní naše měření?

Malé digitální multimetry, které můžeme pro měření použít, mají vnitřní odpor R_V = 1 MΩ. Pro C = 100 μF je časová konstanta T = R_VC = 100 s. Z toho lze odvodit, že za 1 s poklesne napětí na kondenzátoru o 1%. Odečteme-li tedy hodnotu napětí během několika prvních sekund po úderu kladiva na kovadlinu, bude chyba daná vybíjením přes vnitřní odpor voltmetru řádu procent.

Vybíjení kondenzátoru můžeme dokonce s výhodou využít pro kalibraci našeho měření. Kondenzátor s kapacitou 100 mikrofarad je totiž téměř jistě elektrolytický – a u těchto typů kondenzátorů se skutečná kapacita často odchyluje od výrobcem udané hodnoty. (Většinou bývá spíše vyšší.) Chceme-li časy měřit přesněji, musíme určit skutečnou kapacitu. Například tak, že kondenzátor necháme vybíjet do známého odporu a změříme čas, za nějž napětí klesne na jednu e-tinu (tj. na 1/e = 0,3678…) původní hodnoty. Tento čas T se právě rovná časové konstantě RC, odkud již kapacitu C snadno určíme.

Další problém rovněž souvisí s tím, že v zapojení používáme elektrolytický kondenzátor. Nejde jen o to, že musíme dodržet jeho polaritu (u moderních typů elektrolytických kondenzátorů bývá většinou označen minus-pól, ten tedy musíme spojit s minus-pólem baterie). Dielektrikum v elektrolytickém kondenzátoru zůstává částečně polarizováno i po jednorázovém vybití kondenzátoru. Pokud byl kondenzátor nabit např. na plné napětí baterie a my ho vybijeme krátkým zkratováním jeho vývodů, bude na něm napětí opět pomalu růst, i když nebude připojen k žádnému zdroji. Nezapomeňte proto před každým měřením nechat vývody kondenzátoru zkratované dostatečně dlouho.

Další náměty

Již jen stručně uvedeme pár dalších námětů:

• Chceme-li užít jiný než elektrolytický kondenzátor, budeme muset pracovat s kapacitou do cca 1 μF, a budeme proto potřebovat výrazně vyšší vnitřní odpor voltmetru. Toho můžeme dosáhnout např. pomocí operačního zesilovače.

• Pomocí operačního zesilovače můžeme též realizovat zapojení typu „integrátor“, v němž bude závislost mezi časem a napětím lineární i pro vyšší napětí.

• Při měření delších časů je nutno zvýšit kapacitu C nebo odpor R. Naše zapojení bychom pak mohli využít například k měření reakční doby. Pro měření kratších časů musíme naopak R nebo C snížit.

• Dalším námětem, co měřit, může být třeba doba přepálení pojistky. Nebo doba mezi přetržením dvou drátků – tak by například šlo i bez optické závory měřit rychlost nějakého předmětu.

• A ještě zpět k našemu pokusu s kladivem a kovadlinou. Doba rázu vychází kolem milisekundy i méně. Pokud na kovadlinu vložíme např. hřebík a rozklepáváme ze strany jeho hlavičku, doba rázu je delší (i více než desetkrát). Ještě podstatně delší je, klepeme-li na něco opravdu měkkého, např. na kousek cínu.

Závěr

Výhodou popsaného měření je kromě jiného i jeho láce. Rezistor stojí 40 haléřů, kondenzátor několik korun, a dokonce i jednoduchý multimetr lze pořídit za cenu pod sto korun. (V „kamenném“ obchodě je k dostání za 95,- Kč.) Popsané „hrátky“ propojující mechaniku s elektřinou tedy nevyjdou příliš draho…

Literatura

[1] DVOŘÁK, L. Netradiční měřicí přístroje 3. In: Sborník z konference Veletrh nápadů učitelů fyziky 8. JČU České Budějovice 2003, s. 131-137.

[2] http://kdf.mff.cuni.cz/Hrastice

Soustředění, zmiňované v tomto příspěvku, bylo podpořeno grantem FRVŠ B1828/2004 „Rozvoj aktivizujících forem práce ve vzdělávání učitelů matematiky a fyziky“ a rozvojovým projektem MŠMT č.368 „Heuréka II“.