Využití ping-pongových míčků ve fyzice
Ladislav Dvořák
Vývoj vlastností míčků
První míčky byly vyráběny z korku, který byl pokryt síťovinou, aby se zamezilo případným škodám na nábytku a měly průměr 2 palce (asi 50,8 mm). Jelikož měly velmi špatný odskok, byly brzy nahrazeny míčky kaučukovými a následně Jaquesovými tzv. „pružnými“ míčky. Největšího rozvoje se stolní tenis dočkal až po roce 1900, kdy byly zavedeny celuloidové míčky.
U míčků jsou stanoveny nejen jejich hmotnost a průměr, ale i barva a tyto vlastnosti jsou zaneseny v pravidlech stolního tenisu. Tyto hodnoty se během vývoje průběžně upravovaly podle potřeb hráčů a diváků.
Míčky musí být kulaté, vyrobeny z celuloidu nebo z podobné plastické hmoty (stále se vyvíjejí a testují nové materiály), povrch musí být matný a bílé nebo oranžové barvy (pro zelený stůl bílé pro modrý stůl oranžové).
K poslední změně hmotnosti a průměru došlo v roce 2000, kdy hmotnost byla zvětšena z 2,5 g na 2,7 g a průměr z 38 mm na dnešních 40 mm. Tyto změny v pravidlech by měly stolní tenis zatraktivnit pro diváky. Míček by měl létat pomaleji, neměly by vznikat příliš velké rotace a tedy by měla být zvýšena viditelnost míčku.
Na našem trhu jsou k dostání oba poslední typy míčků. Ty větší (2,7 g; 40 mm), které povolují pravidla, tak i ty menší (2,5 g; 38 mm), se kterými se oficiální utkání již hrát nemohou.
Experimenty - využití
1. Vlastnosti látek
1.1. Měření délky
Předložit několik míčků a nechat žáky přeměřit průměry pravítkem a posuvným měřidlem („šuplerou“). Podle výsledků mohou diskutovat např. o přesnosti měření různými měřidly.
1.2. Měření hmotnosti 1
Při výuce hmotnosti můžeme děti nechat zjistit hmotnost míčků a porovnat získané hodnoty z hodnotami, které povolují pravidla. Můžeme je nechat roztřídit míčky na pravidly povolené a nepovolené.
1.3. Měření hmotnosti 2
Protože je známá hmotnost míčků, můžeme je použít jako závaží např. na rovnoramenných vahách.
1.4. Měření hmotnosti 3 - nerovnoramenné váhy
Váhy jsou vytvořeny ze špejle, špendlíku a míčků. Můžeme si zvolit dva způsoby. Na kratším rameni může být vážené těleso a na delším rameni budeme posouvat míčkem nebo obráceně.
Pozn.: je vhodné použít míček o známé hmotnosti, např. 2,5 g.
1.5. Měření objemu
Do odměrného válce vložíme závaží a nalijeme vodu - určíme objem V1. Nyní do odměrného válce do stejného množství vody vložíme míček a zatížíme dříve použitým závažím - určíme objem V2. Objem míčku V získáme odečtením objemu V1 od objemu V2.
Pozn.: z vlastní zkušenosti vím, že změření objemu těles o menších hustotách než hustota použité kapaliny (např. míček, korkový špunt apod.) je pro některé studenty značným problémem.
1.6. Mezimolekulové prostory
Do většího odměrného válce nasypeme míčky a zjistíme objem V1. Do druhého odměrného válce nasypeme např. hrášek - V2. Po přisypání hrášků mezi míčky odečteme objem V a zjistíme, že V1+V2. Podobně je to např. při smíchání vody a lihu.
2. Magnetismus
2.1. Kompas
Do míčku vložit malý válcový magnet a na dně je potřeba míček mírně zatížit pískem apod. Po vložení míčku na vodní hladinu se míček natočí ve směru sever-jih. Jestliže víme, kde je jih (Slunce), můžeme si jednoduše dokreslit na míček světové strany.
3. Mechanika pevných těles
3.1. Těžiště tělesa
Do míčků přilepit různý počet zátěží (písek, olůvka) vložit a po cvrnknutí sledovat jak se míčky pohybují.
3.2. Polohy tělesa
Pomocí míčku a hodinového skla vysvětli polohy: volnou, stálou a vratkou
3.3 Nerovnoměrný pohyb
Míček pustíme po nakloněné rovině.
3.4. Rovnoměrný pohyb
Míček naplněný glycerinem pustíme po mírně nakloněné rovině.
3.5. Páka
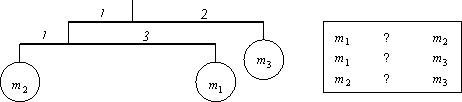
Dva míčky naplníme různým množstvím písku. Po připevnění na nerovnoramennou páku (špejlea špendlík) a změření ramen mohou žáci odvodit poměr mezi hmotnostmi míčků
3.6. Páka 2
Pro ztížení můžeme použít např. 3 míčky viz. obr.
3.7. Volný pád
Jestliže necháme několik míčků naplněných různými materiály (stejný tvar a různá hmotnost) padat ze stejné výšky, dopadnou současně na zem. Rychlost dopadu těles nezávisí na hmotnosti tělesa.
3.8. Pružný ráz
Jestliže vychýlíme krajní z několika bifilárně zavěšených a navzájem se postupně dotýkajících míčků dojde k postupnému předávání energie a odskakování krajních míčků.
3.9. Zákon odrazu
Míček necháme narazit na pevnou překážku a porovnáme úhel dopadu a úhel odrazu (vše se děje v jedné rovině).
3.11. Moment setrvačnosti
Jeden míček vyplníme polystyrénem a doprostřed vložíme ocelovou kuličku. V druhém míčku bude stejná hmotnost rozložena při povrchu míčku. Oba míčky pustíme po nakloněné rovině a sledujeme způsob pohybu.
4. Hydromechanika
4.1. Pascalův ježek
Do míčku napícháme špendlíkem dírky a nasadíme jej na větší injekční stříkačku. Po stlačení pístu můžeme pozorovat, jak voda vystřikuje do všech směrů stejnoměrně.
4.2. Hydrostatická vztlaková síla
Na dno kádinky připevníme kladku, přes kterou je tažena niť od míčku. Na připevněném siloměru můžeme sledovat velikost hydrostatické vztlakové síly.
4.3. Hydrodynamický paradoxon
Na hadici od vodovodního kohoutku nasadíme trychtýř, pustíme vodu a do trychtýře vtlačíme míček. Ten nevypadne protože bude atmosférickou tlakovou silou vtlačován do vrcholu trychtýře.
4.4. Páka pod vodou
Obdoba experimentů 3.5 a 3.6, ale vše umístíme pod hladinu vody. Míčky musí být jen mírně naplněny různým množstvím písku, aby hydrostatická vztlaková síla byla větší než tíhová. Studenty necháme porovnat hmotnosti jednotlivých míčků.
4.5 Plování těles
Míčky různě naplněných pískem vložíme do na sebe nalitých nemísících se kapalin.
4.6. Model vodního mlýnu
Ke kroužku nebo míčku, skrz který vede osa, přilepíme několik půlek míčků. Na tomto modelu můžeme ukázat mlýn na horní i dolní vodu.
5. Aeromechanika
5.1. Dasymetr
Na jednu stranu rovnoramenných vah připevníme míček a na druhou stranu závažíčko o stejné hmotnosti. Po vložení do vývěvy a snížení tlaku dojde k porušení rovnovážného stavu.
5.2. Aerodynamický paradoxon
Obdoba exp. 4.3, kde místo vody použijeme vzduch z plic. Může vyhlásit, kdo z žáků vyfoukne míček nejdále.
5.3. Bernoulliova rovnice
Trubičkou foukneme mezi dva
a) na stole položené míčky
b) zavěšené míčky
Při jinak stejných podmínkách tlak v kapalině klesá s rychlostí jejího proudění
5.4. Bernoulliova rovnice 2
„Přemístěte míček z jedné kádinky na druhou aniž by jste se míčku nebo kádinek dotkli.“ Trubičkou foukáme mírně nad míček, kde vznikne podtlak a míček bude atmosférickou tlakovou silou vtlačován do místa z nižším tlakem.
5.5. Proudění vzduchu za překážkou
Za míček připevněný k podložce postavíme zapálenou svíčku (pozor na hořlavost celuloidu). Jestliže foukneme přes míček, plamen svíčky se nakloní ve směru proudění vzduchu.
5.6. Závislost odporu vzduchu na tvaru tělesa
Na míček (nebo jen půlku) připevněný na špejli otáčivě upevněné k destičce necháme foukat vzduch. Podle úhlu vychýlení může porovnat jednotlivé profily.
5.7. Model větrné elektrárny
Na míček připevněný na špejli přilepíme několik půlek míčků a necháme foukat vzduch např. z fénu.
6.Mechanická energie
6.1. Závislost potenciální energie na hmotnosti těles
Dva míčky o různých hmotnostech necháme padat ze stejné výšky na plastelínu. Podle otisku můžeme porovnat velikosti potenciální energie.
6.2. Závislost potenciální energie na poloze tělesa
Míček necháme padat z různých výšek opět na plastelínu. Podle otisku můžeme porovnat velikosti potenciální energie.
6.3. Závislost kinetické energie na hmotnosti tělesa
Dva míčky o různých hmotnostech necháme koulet ze stejného místa na nakloněné rovině. Po nárazu do překážky a délky jejího posunutí můžeme porovnat velikosti kinetické energie.
6.4. Jo - jo
Ke dvěma půlkám míčku slepené opačně k sobě přivážeme niť. Při pohybu dochází k přeměně energie potenciální na kinetickou a opačně.
6.5. Přeměna energie
Ke dvěma půlkám míčku spojených špejlí připevníme gumičku s přivázaným závažíčkem. Po natočení závažíčka kolem osy se začne soustava pohybovat.
6.6. Ztráta energie?
Míček necháme spadnout z určité výšky a pak zaznamenáváme výšky, do kterých míček odskočí při následujících odrazech od země.
7.Termika
7.1. Závislost přijímaného tepla na vlastnostech povrchu
Do dvou míčků, z nichž jeden bude začerněn, uděláme díry tak, aby se do nich dal vložit teploměr a naplníme je vodou. Pomocí např. plastelíny je postavíme na stůl. Začneme je zahřívat např. rozsvícenou žárovkou a odečítáme teplotu v jednotlivých míčcích.
7.2. Vyhánění „džinů“ z lahve
Hrdlo lahve např. od vína navlhčíme vodou a na hrdlo položíme míček. Poté se k lahvi přiblížíme dlaněmi. Po chvíli se míček začne nadzvedávat - „džinové“ prchají.
7.3. Využití závislosti objemu plynu na jeho teplotě
Mírně promáčknutý (nesmí být prasklý) míček napravíme tak, že jej vložíme do horké vody. Přetlak uvnitř míčku roste v závislosti na teplotě. Po nějaké době míček opět získá tvar koule.
8. Elektrostatika
8.1. Přenesení náboje
Nabitou tyčí se dotkneme zavěšeného míčku s el. vodivým povrchem (obalený alobalem, vodivou stříbřenkou apod.). Míček od tyče po dotyku odskočí.
8.2. Polarizace
Nabitou tyčí se přiblížíme k zavěšenému míčku. Míček k tyči přiskočí a zůstane přichycen.
8.3. Kyvadlo
Mezi dvě elektrody nabíjené např. Kirchhofovou indukční elektrikou vsuneme zavěšený míček s el. vodivým povrchem. Pozorujeme pohyb míčků.
9. Kmitání, vlnění a akustika
9.1. Kmitání
Do půlky míčku uděláme špendlíkem dírku a bifilárně ji zavěsíme. Jestliže ji naplníme vodou, rozkmitáme a pod míčkem budeme rovnoměrným pohybem posunovat pruhem papíru budeme pozorovat sinusoidu vytvořenou odkapávající vodu.
9.2. Příčné kmitání
Na špejli bifilárně vedle sebe zavěsíme několik míčků (12). Po postupném vychýlení můžeme pozorovat vznik vlny.
9.3. Podélné kmitání
Na destičku (např. z kartonu) zavěsíme bifilárně opět několik míčků. Po postupném vychýlení můžeme pozorovat v jednotlivých místech zhuštění a zředění.
9.4. „Míčkohra“
Na několik míčků různě naplněných vodou poklepeme např. dřevěnou tyčinkou.
10. Astronomie
10.1. Modely souhvězdí
Míček rozpůlíme a do jedné půlky napícháme špendlíkem dírky tak, aby vpichy byly ve tvaru vybraných souhvězdí. Pak půlku nasadíme na baterku (38 mm - 40 mm) a skrz míček posvítíme např. na tabuli nebo na zeď.
10.2. Model Země
Míček je potřeba vyplnit např. ocelovými šponami a na povrchu míčku vyznačit světadíly a oceány. Nyní pomocí figurek, např. z magn. šachů, můžeme vysvětlit, že lidé na „spodní“ straně zeměkoule nespadnou, neboť se se Zemí přitahují podobně jako míček a figurky.
10.3. Stín, zatmění
Využijeme „zeměkouli“ z 10.2 o osvítíme ji zdrojem světla. Můžeme vysvětlit vlastní a vržený stín, příp. i zatmění Měsíce.
Závěr
Na myšlenku experimentování s ping-pongovými míčky mě přivedla náhoda. Při suplování tělocviku jsem si všiml, že místy po tělocvičně zůstaly opotřebované promáčknuté, tedy pro hru nepotřebné, ping-pongové míčky. Bylo mi líto je nechat vyhodit, tak jsem přemýšlel, jestli by se nedaly nějakým způsobem ještě využít.
Domnívám se, že využívaní netradičních pomůcek při výuce může hodiny fyziky jen oživit a třeba se na tyto hodiny bude těšit více žáků než doposud.
Literatura:
K 1.8.2004
