Využití mikrofonu k měřením v mechanice
Vladimír Vícha
Anotace:
Mikrofon připojený na zvukovou kartu počítače ve spojení s jednoduchým software (např. AUDACITY) může sloužit k poměrně přesnému měření krátkých časů. Počítač lze následně použít k matematickému zpracování naměřených dat.
Skákání pružného míčku
Úvod
U míčku volně padajícího z výšky několika decimetrů budeme předpokládat platnost zákona zachování mechanické energie (ZZME). Při odrazu od podložky se část kinetické energie změní na vnitřní energii míčku a podložky, proto již míček nevystoupí do původní výšky – ZZME neplatí. Po odrazu vykonává míček vrh svislý vzhůru, při němž již zase ZZME platí.
Koeficient restituce (vzpruživosti) k je poměr rychlosti po odrazu ku rychlosti dopadu. Při výpočtech budeme používat g = 9,81 m·s-2.
Metodické pokyny
Pomůcky: Mikrofon s konektorem (jack) pro připojení do počítače, počítač, program AUDACITY, míček pro stolní tenis.
Úkoly:
1) Sestrojte grafy:
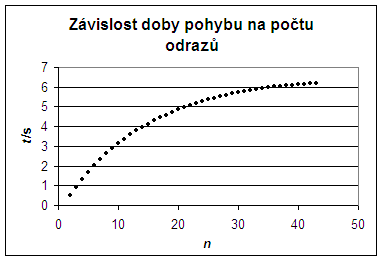
a) závislost doby pohybu na počtu odrazů
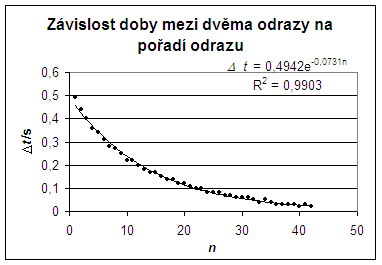
b) závislost doby mezi dvěma odrazy na pořadí odrazu
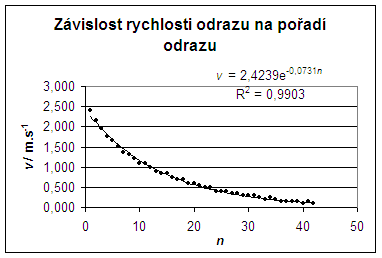
c) závislost rychlosti odrazu na pořadí odrazu
2) Vypočtěte:
d) koeficient restituce metodou regresní funkce
e) dobu celého pohybu pomocí součtu nekonečné řady
Postup: Zasuneme mikrofon do počítače a pomocí: Start - Programy - Příslušenství - Zábava - Záznam zvuku zaznamenáme skákání míčku na tvrdé vodorovné podložce. Počáteční výšku volíme do 0,5 m. Naměřený soubor je ve formátu wav a je třeba jej uložit.
Na internetu je na adrese http://audacity.sourceforge.net/ volně dostupný ke stažení program AUDACITY. Stáhneme jej a prověříme antivirovým programem. Po spuštění otevřeme námi naměřený soubor. Měli bychom vidět podobný průběh:

Pomocí nástroje lupasi zvětšíme potřebnou část grafu.

V menu View – Zoom out se lze vrátit k předchozí velikosti. Klikneme na ikonu, a umístíme kurzor na záznam prvního nárazu. Po kliknutí se vlevo dole za nápisem Cursor objeví číslo se šesti desetinnými čísly udávající čas. Čas zaokrouhlíme na setiny sekundy. Takto ze záznamu odečteme časy pro sestrojení požadovaných grafů.
Tabulka 1 ukazuje časy dopadu t a časy mezi dopadem a odrazem t pro prvních 11 dopadů (pro grafy je využito 43 dopadů).
Výsledky 1
| odraz |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| t/s |
7,65 |
8,14 |
8,57 |
8,96 |
9,33 |
9,67 |
9,98 |
10,26 |
10,53 |
10,77 |
11,00 |
| t/s |
0,49 |
0,43 |
0,39 |
0,37 |
0,34 |
0,31 |
0,28 |
0,27 |
0,24 |
0,23 |
|
| v/ m/s |
2,403 |
2,109 |
1,913 |
1,815 |
1,668 |
1,521 |
1,373 |
1,324 |
1,177 |
1,128 |
|
| k |
0,88 |
0,91 |
0,95 |
0,92 |
0,91 |
0,90 |
0,96 |
0,89 |
0,96 |
průměr |
0,92 |
Tabulka 1
Rychlost odrazu je vypočtena ze vzorců pro vrh svislý vzhůru:v = g · Δt/2.
Výsledky 2
Koeficient restituce byl v tabulce 1 vypočten pro každé dva následující časy a pak určena průměrná hodnota. Vhodnější však je vypočítat pomocí Excelu regresní funkci. Dobře vyhovuje exponenciální funkce v = 2,4239 · e-0,0731 n s koeficientem determinace R2 = 0,9903. Protože definiční obor funkce je podmnožinou přirozených čísel, jedná se o posloupnost a to geometrickou. Kvocientem posloupnosti je právě hledaný koeficient restituce
![]() .
.
Geometrická posloupnost s kvocientem e-0,0731 vystihuje také závislost doby mezi odrazy na počtu odrazů Δt = 0,4942 · e-0,0731 n, R2 = 0,9903. Posloupnosti odpovídá konvergující geometrická řada. Její součet určíme podle vzorce
![]() = 6,56 s.
= 6,56 s.
Součet nekonečné řady pro nás představuje celkovou dobu pohybu míčku.
Závěr: Z grafů vyplývá, že rychlost po každém dopadu exponenciálně klesá, jde o geometrickou posloupnost. Doba mezi dvěma odrazy je také geometrická posloupnost se stejným kvocientem, součet časů konverguje.
Volný pád těles
Úvod
Železné matky navázané na provázek způsobují při dopadech zvuky, které lze snímat mikrofonem do počítače. V závislosti na rozložení matek na provázku, mohou zvuky přicházet nerovnoměrně, ale i rovnoměrně.
Metodické pokyny
Pomůcky: Mikrofon s konektorem (jack) pro připojení do počítače, počítač, program AUDACITY, železné matky (M10) na provázku.
Úkoly:
1) Zaznamenejte mikrofonem dopad matek rozložených na provázku rovnoměrně a s rostoucími vzdálenostmi.
2) Do grafů proveďte záznam pro oba typy pokusů
Postup: Šest větších matek navážeme na tenký provázek po 25 cm. Provázek uchopíme tak, aby se spodní matka dotýkala podložky, blízko níž je mikrofon. Počkáme, až se kývání matek zklidní a provázek uvolníme. Záznam zvuku do počítače a odečtení časů provádíme programem AUDACITY (viz výše). Jako podložka se osvědčily složené noviny, vzdálenost mikrofonu je třeba vyladit.
Pět matek navážeme tak, že rostou jejich vzdálenosti směrem vzhůru:
10 cm – 30 cm – 50 cm – 70 cm
Provedeme volný pád, odečteme časy.
Výsledky:Záznam zvuku v programu AUDACITY

6 matek rozložených rovnoměrně po 25 cm (5 dopadů)

5 matek rozložených s rostoucími vzdálenostmi (4 dopady)
Odečtené hodnoty času a grafy:
| pořadí dopadu |
t/s |
| 1 |
1,535 |
| 2 |
1,637 |
| 3 |
1,706 |
| 4 |
1,764 |
| 5 |
1,815 |
Tabulka č. 1
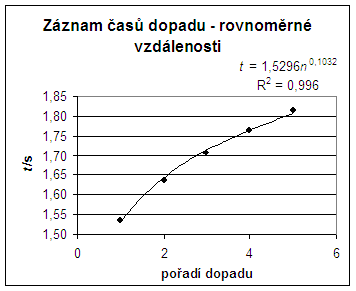
Graf č. 1
| pořadí dopadu |
t/s |
| 1 |
1,537 |
| 2 |
1,647 |
| 3 |
1,781 |
| 4 |
1,923 |
Tabulka č. 2
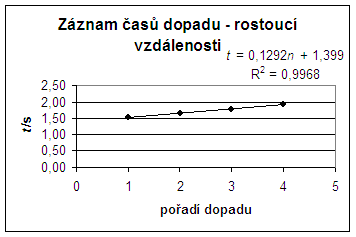
graf č. 2
Závěr: Z grafu č. 1 vyplývá, že volný pád je zrychlený pohyb. Matky jsou rozloženy rovnoměrně a přitom každá následující dopadá za kratší časový interval.
Z grafu č. 2 vyplývá, že když vzdálenosti matek od první matky rostou kvadraticky (10 cm, 40 cm, 90 cm, 160 cm), jsou intervaly mezi dopady pravidelné. To potvrzuje, že volný pád je rovnoměrně zrychlený pohyb s = 1/2 gt2
