Pružné či nepružné beranidlo?
Jan Koupil
Jedná se o jednoduchý experiment, při kterém se snažíme shodit postavený kvádr koulí na závěsu (jako bychom bourali zeď). Kyvadlo je tvořeno závěsem a buď pružnou nebo nepružnou koulí. S jeho pomocí demonstrujeme, že stejná počáteční výchylka (tedy stejná energie) kyvadla může v případě jednoho kyvadla stačit pro zbourání a v případě druhého ne.
Úlohu je možné podrobněji zkoumat a zjistit například koeficient restituce.
Původní nápad na experiment pochází z časopisu The Physics Teacher [1].
Vyrážet dveře pružným či nepružným beranidlem?
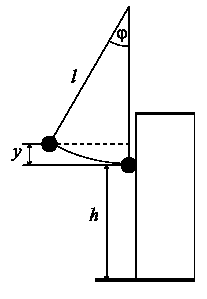
obr. 1 – uspořádání experimentu
Když ve fyzice mluvíme o zákonu zachování hybnosti, popřípadě o pružných a nepružných srážkách, a dáváme příklady jako odraz tenisového míčku od stěny a podobně, není nezajímavé položit otázku, zda bude na stěnu působit větší silou stejně těžký pružný míček (tenisák), který se odrazí, nebo nepružný (baseballový), který pouze spadne na zem. Pokud jsou studenti „příliš“ chytří, můžeme se je pokusit zmást tvrzením, že při pružné srážce se míček vrací s původní energií, žádnou tedy patrně nepředal, zatímco při nepružné sice předává jen polovinu hybnosti, ale energii ztratí všechnu. Ať tedy rozhodnou, zda „bourá hybnost nebo energie.“
Pro rozsouzení sporných názorů použijeme jednoduchý experiment. Kyvadlo zavěsíme na bifilární závěs tak, aby se ve svislé poloze dotýkalo kvádru postaveného na nejužší stěnu (obr. 1). Závaží kyvadla je tvořeno z jedné strany pružným a z druhé nepružným materiálem (např. ocelová kulička napůl obalená plastelínou), otočením závaží tedy můžeme zvolit, zda dojde k pružné nebo nepružné srážce, přičemž hmotnost kyvadla je v obou případech evidentně stejná. Ze zkušenosti vychází, že závěs kyvadla je vhodné volit minimálně dvakrát delší, než je výška kvádru, a to tak, aby kyvadlo do kvádru naráželo v horní třetině. Jinak bychom museli kyvadlo vychylovat do příliš velkých úhlů, kde jsou měření nepřesná.
Pokud kyvadlo vychýlíme málo, pouze se od kvádru odrazí, od určitého úhlu vychýlení jej ale povalí. Otočením závaží můžeme snadno demonstrovat, že počáteční vychýlení kyvadla (a tedy energie) dostačující k povalení při pružné srážce je znatelně menší než při srážce nepružné.
Matematické řešení problému
Půjdeme-li více do hloubky, zjistíme, že problém je zajímavý i z jiného pohledu. Jedná se o komplikovanější, ale středoškolsky řešitelnou úlohu, ve které se potká několik částí mechaniky – zákony zachování, rotace tuhého tělesa a problém stability tělesa. Navíc můžeme v rámci laboratorních prací či semináře provést i nějaká měření, viz níže.
Celý děj rozdělíme na tři menší části – jsou jimi pohyb kyvadla (přeměna mechanické energie), předání momentu hybnosti a stabilita kvádru.
Kyvadlo
V první fázi se potenciální energie kyvadla přemění na kinetickou. Ztráty mechanické energie v této fázi zanedbáme. Ze znalosti počátečního úhlu a délky závěsu můžeme tedy snadno zjistit rychlost, kterou kulička narazí do kvádru. Zákon zachování mechanické energie pro náš případ zní
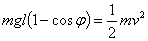 .
.
V tomto vztahu zanedbáváme rotační energii kuličky, která je však řádově nižší než uvažované energie a do výsledků se tedy měřitelně nepromítne.
Předání momentu hybnosti
Po nárazu na kvádr se kulička odrazí zpět rychlostí 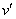 , která je menší než rychlost nárazu v. Poměr mezi velikostmi rychlostí k nazýváme koeficient restituce.
, která je menší než rychlost nárazu v. Poměr mezi velikostmi rychlostí k nazýváme koeficient restituce.
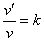 .
.
Současně se začne pohybovat také kvádr. Pro jednoduchost zanedbáme možný posuvný pohyb a budeme předpokládat pouze otáčení kolem osy (překlopení). Zákon zachování momentu hybnosti tedy bude vypadat
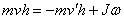 ,
,
kde h je výška místa kontaktu kuličky a kvádru, J jeho moment setrvačnosti kvádru vzhledem k ose otáčení vedoucí hranou a w úhlová rychlost kvádru těsně poté, co do něj kulička narazila. Člen s rychlostí 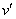 má záporné znaménko, tato rychlost má opačný směr než původní rychlost v. Všechny momenty v předchozím vztahu bereme vůči ose otáčení kvádru. Po dosazení tedy dostaneme vztah
má záporné znaménko, tato rychlost má opačný směr než původní rychlost v. Všechny momenty v předchozím vztahu bereme vůči ose otáčení kvádru. Po dosazení tedy dostaneme vztah
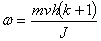 .
.
Stabilita kvádru
Aby došlo k překlopení kvádru, musí se jeho těžiště zvednout nad bod otáčení, tzn. z původní výšky 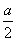 do výšky
do výšky 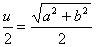 . Příslušné změně potenciální energie musí odpovídat počáteční kinetická energie kvádru Ek. Podmínku pro překlopení proto vyjádříme jako
. Příslušné změně potenciální energie musí odpovídat počáteční kinetická energie kvádru Ek. Podmínku pro překlopení proto vyjádříme jako
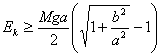 .
.
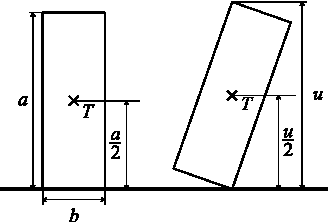
Obr. 2 – překlopení kvádru
Počáteční kinetická energie rotace kvádru je vyjádřena vztahem
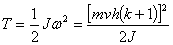 .
.
Velikost momentu setrvačnosti 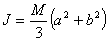 najdeme v tabulkách, určíme ze Steinerovy věty nebo integrací.
najdeme v tabulkách, určíme ze Steinerovy věty nebo integrací.
A všechno dohromady …
V našem případě známe všechny hmotnosti, rozměry a délky. Opakovanými pokusy můžeme změřit mezní úhel vychýlení kyvadla, při kterém se kvádr právě překlopí, Jedinou neznámou zůstává koeficient restituce, který nám říká „jak je srážka pružná.“ Po několika algebraických úpravách dostaneme pro koeficient restituce dlouhý vztah
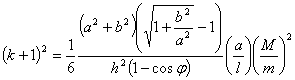 ,
,
Střet teorie s praxí
K ověření teorie jsem použil dřevotřískovou desku a zmiňovanou ocelovo-plastelínovou kuličku. Provedl jsem větší množství experimentů s různými délkami závěsu (čím delší je závěs, tím menší je mezní úhel). Pokusy byly natočeny na videokameru a teprve následně vyhodnoceny. Z videozáznamu bylo snadné odečíst jak mezní úhel, tak úhel do kterého kulička vystoupí po odrazu a tím pádem určit koeficient restituce dvěma různými způsoby.

Obr. 3 – měření mezního úhlu na snímku z videozáznamu
Při pružném odrazu a malých výchylkách (do 30°-40°) je shoda dobrá, koeficient restituce vychází zhruba 0,75 oběma metodami, přičemž chyba měření je přibližně 0,1. Při větších výchylkách (tzn. od 40° výše, měřeno bylo při úhlech až do 70°) vychází koeficient vypočtený z mezního úhlu (zhruba 0,7) systematicky větší než změřený z videozáznamu (0,6-0,5), což lze vysvětlit tím, že kyvadlo není ideální. I bez nárazu na desku, při pouhém kývání je zřejmé, se kyvadlo nevrací do původní výšky.
Při měření nepružného odrazu vychází metodou výpočtu z mezního úhlu koeficient restituce (0,24 ± 0,3) a tato hodnota se také při větších počátečních výchylkách kyvadla zvětšuje, přičemž hodnoty mezních úhlů jsou při jinak stejných podmínkách zhruba o 15° větší. Metodu přímého měření z videozáznamu nelze v případě kyvadla s kuličkou z oceli a plastelíny dobře použít, protože plastelína nemá kulový tvar, kyvadlo se tak odráží do různých směrů a mnoho energie se ztrácí.
Něco k měření
Při skutečném měření, kdy chceme z experimentu dostat více, než jen fakt, že pružnou stranou kyvadla bouráme efektivněji než nepružnou, se objeví několik technických problémů. Zejména je třeba dát pozor na tyto věci:
• Podložka by měla být ve vodorovné rovině.
• Kvádr je dobré mírně zapřít (například tenkou tyčkou či dvěma špendlíky přilepenými na podložce, aby se při měření neposouval, pouze překlápěl).
• Kvádr musí být skutečně kvádrem. Pokud nejsou jeho hrany kolmé, má tendenci se kácet i na stranu ze které do něj kulička narazila. Toto je patrně nejnáročnější podmínka.
• Kyvadlo by mělo do kvádru narážet v nejnižším bodě své dráhy a to kolmo na stěnu kvádru, v její ose (uprostřed), jinak je efektivita nižší, mezní úhel roste a kyvadlo se má tendenci zmítat.
• Pokud se rozhodnete experiment natáčet, je třeba mít kameru velmi přesně nastavenu kolmo k rovině kývání.
Pokud byste zatoužili po dokonalejším kyvadle, je možné zakoupit v online obchodě Arbor Scientific [2] za cca 3 $ sadu dvou stejně vypadajících černých míčků, pružného a nepružného, ty rozříznout, vložit mezi ně vlákno a slepit. Vzniklá kulička pak vypadá z obou stran zcela stejně, jen odrazivost je jiná.
Literatura
[1] Micklavzina S.: Impulse Demonstration Using a 'Half-Bouncy' Ball, The Physics Teacher, Vol. 34, no. 4, p. 253, April 1996
[2] Arbor Scientific, Happy and unhappy balls [http://www.arborsci.com/detail.aspx?ID=362]
