Motivačné pokusy z mechaniky
Ľubomír Machovič, Ivan Baník
Abstrakt: Príspevok uvádza niekoľko námetov na jednoduché motivačné fyzikálne experimenty z mechaniky. Ide o tri „exotické“ kyvadlá. Pokusy sa dajú realizovať aj v bežných domácich podmienkach. Majú prispieť k eliminácii nežiaducej mechanickej formy štúdia mechaniky a zvýrazniť vlastný fyzikálny obsah príslušného učiva.
Exotické kyvadlá
Štipcové fyzikálne kyvadlo
V domácich podmienkach sa dá ľahko zhotoviť „exotické“ fyzikálne kyvadlo, aké vidíme na obr. 1. K tomu potrebujeme ihlu, limo-trubičku a dva, prípadne viac štipcov na bielizeň. Ide teda o bežne dostupné drobnosti, aké sa nájdu v každej domácnosti.
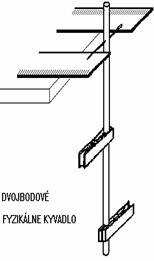
Obr. 1
Kyvadlo, o ktorom je reč, je jednoduché nielen pokiaľ ide o jeho zhotovenie. Je to vlastne v istom zmysle najjednoduchšie možné fyzikálne kyvadlo (ak odhliadneme od jednobodového, a teda matematického kyvadla). Je to v podstate dvojbodové kyvadlo - tvorené dvoma hmotnými „bodmi“ a „nehmotnou“ limo-trubičkou. Hmotnosť limo-trubičky je totiž o rád menšia, ako hmotnosť bežného štipca. Trubička má napr. hmotnosť 0,6 g, zatiaľ čo dva štipce spolu hmotnosť okolo 12 g.
Štipcové kyvadlo sa zhotoví veľmi ľahko. Ihlu prebodneme cez limo-trubičku kolmo na trubičku. Potom na trubičku pripneme dva, resp. viac štipcov tak, aby ich pozdĺžne osi boli rovnobežné s ihlou. Za takýchto podmienok sa štipce dajú považovať za hmotné body. Aby naše kyvadlo bolo schopné na ihle kmitať, treba jeho štipce pripnúť na limo-trubičku s opačnou orientáciou (v protismere). To preto, aby ťažisko sústavy nevybočilo mimo limo-trubičky. Ináč by sústava visela iba na jednom konci ihly a druhý by bol voľný. Kmitanie by nebolo možné.
Takto pripravené kyvadlo zavesíme na dve „nosné“ ramená. Môžu to byť dve knihy a či dve pravítka, ktorých konce prečnievajú za okraj stola. Vhodným držiakom štipcového kyvadla je však aj špeciálny „štipcový držiak“. Je to pravítko s dvoma ďalšími pomocnými štipcami, ktoré prichytíme na koniec pravítka tak, aby vytvorili dve rovnobežné nosné „lišty“ v smere pozdĺžnej osi pravítka. Pravítko potom položíme na stôl tak, aby svojim koncom spolu so štipcami prečnievalo za okraj stola. Ak na štipcový držiak zavesíme štipcové kyvadlo a vychýlime ho z rovnovážnej polohy, bude po uvoľnení konať kmity okolo osi určenej ihlou. Kyvadlo je hotové.
S opísaným kyvadlom môžeme vykonať poučné konfrontačné merania, ktoré väzia v tom, že pre dané polohy štipcov určíme periódu kyvadla najprv teoretickým výpočtom a zistenú hodnotu potom overíme priamym meraním. Keďže hmotnosť limo-trubičky je v porovnaní s hmotnosťami štipcov veľmi malá, môžeme ju pri výpočte zanedbať. Vďaka tomu je potom výpočet veľmi jednoduchý. Každý štipec (ktorého pozdĺžna os je rovnobežná s ihlou), môžeme totiž v dobrom priblížení považovať za hmotný bod hmotnosti m1. Tú však pri počítaní periódy nemusíme poznať, lebo po dosadení vypadne. Napriek jednoduchosti je fyzikálna podstata veci však zachovaná.
Pri teoretickom výpočte periódy T vychádzame zo vzťahu
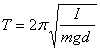
kde d je vzdialenosť ťažiska od osi otáčania, m hmotnosť kyvadla, g tiažové zrýchlenie a moment zotrvačnosti vzhľadom na os otáčania 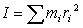 . Sumácia sa všeobecne vzťahuje na všetky štipce (ako hmotné body). Ak ide o rovnaké štipce bude mi = m1. Vzdialenosti ri jednotlivých štipcov od osi o otáčania zmeriame. Takže
. Sumácia sa všeobecne vzťahuje na všetky štipce (ako hmotné body). Ak ide o rovnaké štipce bude mi = m1. Vzdialenosti ri jednotlivých štipcov od osi o otáčania zmeriame. Takže 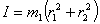 . K výpočtu periódy je potrebné určiť ešte aj polohu ťažiska kyvadla. Vzdialenosť d určíme buď experimentálne alebo výpočtom. Pri experimentálnom spôsobe podopierame kyvadlo (odňaté z držiaka) v rôzných miestach, až dosiahneme rovnováhu. Nesmieme však pohnúť štipcami.
. K výpočtu periódy je potrebné určiť ešte aj polohu ťažiska kyvadla. Vzdialenosť d určíme buď experimentálne alebo výpočtom. Pri experimentálnom spôsobe podopierame kyvadlo (odňaté z držiaka) v rôzných miestach, až dosiahneme rovnováhu. Nesmieme však pohnúť štipcami.
Pri teoretickom spôsobe vychádzame z nameraných vzdialeností jednotlivých štipcov od osi otáčania. Pre dva rovnaké štipce sa vzdialenosť d rovná priemernej vzdialenosti štipcov od osi. Ak do vzťahu (1) dosadíme za d = (r1 + r2)/2 a za hmotnosť kyvadla m = 2m1, potom pre jeho periódu dostaneme vzťah
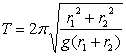
Pri experimentálnom určení periódy postupujeme tak, že zmeriame dobu desiatich kmitov. Ak budú podmienky experimentu dostatočne blízke uvedeným teoretickým predpokladom, dostaneme veľmi dobrý súhlas teórie s experimentom.
Podobným spôsobom vykonáme konfrontačné merania aj pre iné polohy štipcov na limo-trubičke. Ak to poloha ihly na trubičke dovoľuje, umiestníme jeden zo štipcov nad ihlu. Takto sa ťažisko sústavy priblíži k ihle, čím sa dosiahne pomalšie kmitanie.
Tiež matematické kyvadlo?
Hmotný bod na nehmotnom vlákne. Tak, alebo podobne sa píše v niektorých knihách o matematickom kyvadle,v podstate je to pravda. A čo tak namiesto hmotného bodu a nehmotnej nite niečo celkom iné, povedzme tenkú trubičku (resp. tyč) zavesenú na nitiach spôsobom znázorneným na obr. 3, alebo knihu zavesenú tak, ako to ukazuje obr. 2.
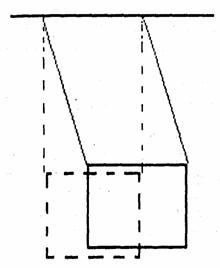
Obr. 2
Čitateľa asi prekvapí konštatovanie, že také kyvadlá budú kmitať v súhlase so vzťahom pre matematické kyvadlo, hoci tu ani zďaleka nejde o hmotný bod. Periódy takýchto kyvadiel sa budú počítať zo vzťahu
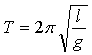
pričom l je dĺžka príslušných nití. Čudné, však?
Na zavesenie knihy je vhodné použiť uzavretú slučku nite, čo je z praktického hľadiska výhodné. Tá prechádza tak zavesenou kmitajúcou knihou, ako aj knihou-držiakom, položenou na stole pri jeho okraji. Kniha sa na niti drží v podstate sama.
S uvedenými „kvázi-matematickými“ kyvadlami sa dá aj merať napríklad zrýchlenie voľného pádu (metódou matematického kyvadla). Inou otázkou je, ako to všetko, čo sme o našich čudných matematických kyvadlách povedali, zdôvodniť?
Ak sa nad vecou trochu zamyslíme, prídeme na to, že ťažisko knihy sa pohybuje po oblúku kružnice, ktorej polomer sa presne rovná dĺžke závesných nití. To sa dá vlastne povedať o každom bode knihy. Už aj to veľa napovedá. Kinetická energia knihy - keďže ide o postupný pohyb - sa dá vyjadriť tiež rovnako, ako pri hmotnom bode. Potenciálna energia kyvadla bude taktiež mgh, rovnako ako pri hmotnom bode, pričom h je „zdvihnutie“ ťažiska knihy (a vlastne aj hociktorého jej bodu) nad jeho úroveň v najnižšej polohe.
Vidíme, že pri kyvadle s knihou sa to všetko veľmi podobá hmotnému bodu na niti. Pri vychýlení kyvadla z rovnovážnej polohy o uhol φ, budú obe formy mechanickej energie vyjadrené analogickým spôsobom, ako pri hmotnom bode a nehmotnej niti. Nuž nečudo, že kyvadlá budú mať aj rovnakú periódu.
Dvojniťové torzné kyvadlo
Pod dvojniťovým kyvadlom budeme rozumieť teleso zavesené v homogénnom gravitačnom poli na dvoch zvislých, navzájom rovnobežných a rovnako dlhých nitiach (obr. 3). Vzájomná vzdialenosť týchto nití je d a ich dĺžka l. V nami uvažovaných prípadoch budeme predpokladať, že ťažisko T telesa sa v stave rovnováhy nachádza na „strednej“ priamke o určenej oboma niťami. Obe nite budú v stave pokoja napínané rovnakou silou, rovnajúcou sa polovici tiaže telesa. Naviac, v našich experimentoch budeme využívať telesá, ktoré sú symetrické vzhľadom na priamku o. Napínanie oboch nití je potom rovnaké aj pri kmitaní.
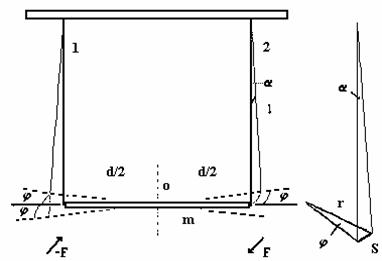
Obr. 3
Perióda kmitov
Ak dané teleso pootočíme o istý neveľký uhol φ okolo osi o a v takom stave ho uvoľníme, začne kmitať s periódou T, pre ktorú - ako ukážeme neskôr - platí
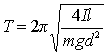
kde I je moment zotrvačnosti telesa vzhľadom na os o, m je jeho hmotnosť a g je tiažové zrýchlenie.
Uvedený vzťah (4) možno získať zo vzťahu pre periódu torzného kyvadla
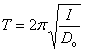
kde Do je direkčný moment kyvadla.
Analýzou síl, ktoré pôsobia na zavesené a pootočené teleso, získame pre veľkosť momentu pôsobiacich síl vyjadrenie
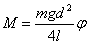
Porovnaním so vzťahom M = Doφ, potom vychádza
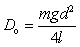
Dosadením za Do do tradičného vzťahu (5) pre periódu torzného kyvadla dostaneme horeuvedený vzťah (4) pre periódu dvojniťového torzného kyvadla. Na jeho základe možno s dvojniťovým kyvadlom vykonať meranie momentu zotrvačnosti.
Moment zotrvačnosti tenkej homogénnej tyče vzhľadom na os o je 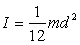 , kde m je hmotnosť tyče a d jej dĺžka. Po dosadení za I do vzťahu (4) pre periódu vypadne ako dĺžka tyče d tak aj jej hmotnosť m:
, kde m je hmotnosť tyče a d jej dĺžka. Po dosadení za I do vzťahu (4) pre periódu vypadne ako dĺžka tyče d tak aj jej hmotnosť m:
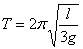
Tento vzťah možno využiť aj na meranie tiažového zrýchlenia.
Literatúra
[1] Baník I a kol.: Fyzika netradične 1. Vyd. STU Bratislava, Bratislava 1997.
