Odpor vzduchu
Jakub Benda, Milan Rojko
V kroužku experimentální fyziky jsme ověřovali vztah:
F = ½ SCρv2
V tomto vztahu je
F odporová aerodynamická síla působící na těleso obtékané tekutinou,
S plošný obsah průřezu kolmý na směr rychlosti,
ρ hustota tekutiny,
v rychlost obtékání a
C tvarový faktor, tzv. součinitel odporu.
Tato rovnice běžně uváděná v učebnicích jako Newtonův vztah pro aerodynamickou odporovou sílu se dá odvodit jednoduchým způsobem [1]:
Uvažujme těleso pohybující se v tekutině rychlostí v. Maximální (tzv. stínový) průřez tělesa ve směru kolmém na směr rychlosti v označme S. Toto těleso za čas Δt opíše objem
ΔV = SvΔt
Při tomto pohybu rozpohybuje i tekutinu, kterou má v cestě. Hmotnost této tekutiny je nepochybně
Δm = ρΔV = ρSvΔt
a tedy dodaná (kinetická) energie
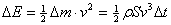
Abychom udrželi těleso v rovnoměrném pohybu při dané odporové síle, musí být náš výkon
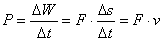
tedy
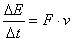
Po dosazení do vztahu (3) za energii podle (2) dostáváme
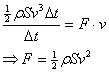
Tato úvaha byla samozřejmě značně zjednodušená. Například v předpokladu, že těleso uvede do pohybu pouze tekutinu, která odpovídá jeho průřezu. Ve skutečnosti tomu tak téměř nikdy není. Vztah je tedy proto doplňován tzv. tvarovou konstantou C (součinitel odporu), která funguje jako experimentálně zjištěná korekce účinného průřezu daného předmětu.
Tento vztah jsme nejdříve ověřili jednoduchými prostředky pro obtékání kruhové destičky vzduchem. V druhé fázi jsme hledali hodnotu součinitele C pro 5 různých těles různých tvarů ale stejné hmotnost.
K získání proudu vzduchu jsme použili běžný fén. Z klasických laboratorních stojanů jsme vytvořili přibližně dva metry vysoký stativ (na ilustračním foto je zkrácený), a v jeho spodní části jsme upevnili fén. Ze středu jeho ústí bylo svisle napnuto tenké vlákno, které sloužilo jako vedení pro tělesa vystavená tlakové síle proudícího vzduchu (viz. obr.1).
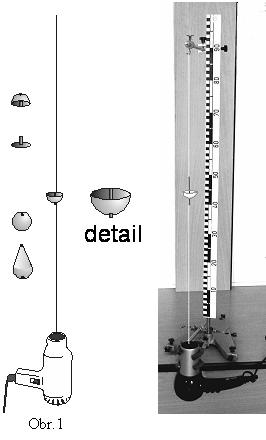
Při prvních pokusech jsme používali jako vodící vlákno tenký pozinkovaný drátek. Fluktuace v proudění vzduchu ale způsobovaly, že i při konstantních podmínkách byla poloha tělesa na drátě silně nestabilní (neustále se pohybovalo s vertikální odchylkou až 10 cm). Tyto fluktuace se podařilo snížit použitím textilního vlákna na polovinu.
K pokusům jsme použili různě těžké kruhové kotoučky s průměrem 38 mm a 5 stejně těžkých tělísek shodného průřezu.
Středem každého z těles procházela vodící trubička - kousek náplně do propisky, kterou jsme pečlivě vyčistili lihem. (viz obr.2)


Obr.2
Tab.1 hmotnosti těles.
| těleso |
4 tělíska |
kotouč 1 |
kotouč 2 |
kotouč 3 |
kotouč 4 |
kotouč 5 |
kotouč 6 |
kotouč 7 |
| Hmotnost [g] |
3,55 |
0,62 |
1,07 |
2,19 |
3,20 |
3,55 |
7,80 |
12,02 |
| tíhová síla [mN] |
34,8 |
6,08 |
10,5 |
21,5 |
31,4 |
34,8 |
76,5 |
118,1 |
Princip námi zvolené metody je jednoduchý.
Anemometrem změříme velikost rychlosti proudu vzduchu v různé vzdálenosti od ústí fénu. Vystavíme-li pak těleso dané hmotnosti proudu vzduchu, „ustálí“ se s přijatelnými fluktuacemi v takové poloze, při níž je tlaková síla proudícího vzduchu v rovnováze s tíhovou silou na něj působící.
Výsledky měření rychlosti proudu vzduchu v v závislosti na vzdálenosti od ústí fénu uvádí Tab.2 a graf na obr.3.
Tab.2
| vzdálenost od ústí [cm] |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
| rychlost vzduchu [m×s-1] |
16,4 |
11,7 |
11,1 |
9,4 |
8,4 |
7,0 |
6,3 |
4,6 |
3,8 |
3,0 |
2,0 |
1,9 |
1,6 |
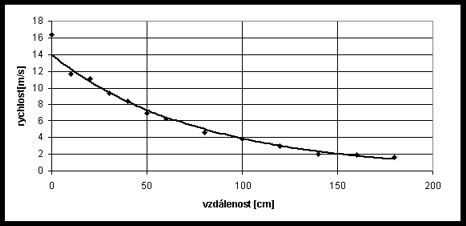
Obr.3
Získaný průběh je, s výjimkou nejbližší vzdálenosti od fénu, blízký exponenciální křivce, pro kterou nám Excel poskytnul rovnici v = 14·e-0,0128x. Podle tohoto vztahu pro vzdálenost x od ústí fénu v centimetrech vychází rychlost vzduchu v v metrech za sekundu.
Výsledky měření výšek ve kterých se „ustálil“ kotouček dané hmotnosti a odpovídající rychlost přiřazenou uvedenou exponenciální funkcí popisuje Tab.3.
Tab.3.
| číslo kotoučku |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| vzdálenost od ústí [cm] |
175 |
129 |
90 |
64 |
62 |
25 |
4 |
| rychlost vzduchu [m×s-1] |
1,5 |
2,7 |
4,5 |
6,2 |
6,3 |
10,2 |
13,2 |
Graf na obr.4 ukazuje závislost v2(F)
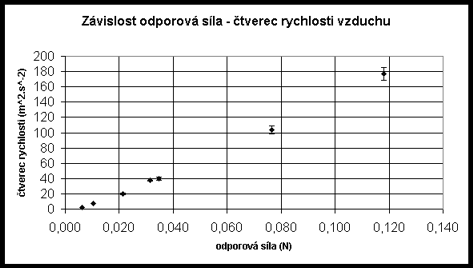
Obr.4
Linearita grafu na obr.4 dostatečně průkazně ukazuje, že v námi proměřovaném intervalu rychlostí je Newtonův vzorec použitelný pro popis závislosti odporové síly na rychlosti.
Ze směrnice tohoto grafu 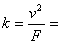 1560 m×kg-1 můžeme ještě odhadnout součinitele odporu C kruhové destičky.
1560 m×kg-1 můžeme ještě odhadnout součinitele odporu C kruhové destičky.
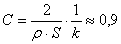 , což je hodnota, která leží v oblasti hodnot, které jsou pro kruhovou desku uváděny v literatuře.
, což je hodnota, která leží v oblasti hodnot, které jsou pro kruhovou desku uváděny v literatuře.
Výsledky druhé skupiny měření pro určení součinitelů odporu C jednotlivých těles jsou přehledně zachyceny v následující tabulce.
Tab.4
|
|
vzdálenost od fénu [m] |
rychlost vzduchu [m×s-1] |
rychlost vzduchu2 [m2×s-2] |
součinitel odporu
|
|
|
0,005 |
16 |
256 |
0,2 |
|
|
0,03 |
13 |
169 |
0,3 |
|
|
0,17 |
11 |
121 |
0,4 |
|
|
0,62 |
6,3 |
40 |
0,9 |
|
|
0,68 |
5,8 |
34 |
1,3 |
Chyby při popisových měřeních jsou v rozhodující míře jsou dány nepřesným určením „rovnovážných“ poloh těles. Chyba ve stanovení těchto vzdálenosti od fénu klesala od pěti centimetrů u největší vzdálenosti (pro nejlehčí kruhovou destičku) až k milimetrové hodnotě pro kapkovitý tvar. Chybové úsečky v grafu na obrázku 4 i výsledné hodnoty pro součinitele C ukazují, že tyto nepřesnosti kvalitativně výsledek neovlivňují.
Nakonec drobná poznámka pro ty, kteří by podobné měření chtěli provádět. Obtížnější je optimální nastavení svislého vodícího vlákna do osy vzduchového proudu z fénu. Nám se to podařilo nejlépe tak, že jsme vlákno s nejlehčím kotoučkem upevnili do směru, ve kterém kotouček vystoupal do největší výšky.
Literatura:
[1] Vybíral, B., Zdeborová, L.: Odporové síly, MAFY Hradec Králové 2001 s. 20





