Riešenie úloh Turnaja mladých fyzikov pomocou programu IP-Coach
Pavol Kubinec
Abstrakt
Na konkrétnych príkladoch referujeme o možnostiach programu IP-Coach pri riešení úloh súťaže „Turnaj mladých fyzikov“. Program využívame na modelovanie riešení úloh a na meranie hodnôt rôznych fyzikálnych veličín pomocou vhodných senzorov.
1 Turnaj mladých fyzikov
Rozvíjanie fyzikálneho myslenia žiakov je dlhodobý proces. Okrem vyučovacích hodín je dobré tento proces rozvíjať aj v mimoškolských aktivitách. Jednou z vhodných možností sa nám javí súťaž Turnaj mladých fyzikov (TMF). V nej sa riešia netradičné fyzikálne problémy, ktoré často presahujú rozsah stredoškolskej fyziky. Súťaž ponúka možnosť zapojenia aj pre matematicky menej zručných študentov. Stačí dobrý nápad či technická zručnosť. Navyše TMF je kolektívna súťaž, kde sa žiaci učia navzájom spolupracovať a tešiť sa z úspechov.
Turnaj mladých fyzikov je súťaž pre päťčlenné družstvá stredoškolákov [1], ktorých vedie spravidla ich učiteľ fyziky. Úlohou súťažiacich je vypracovať riešenia 17 úloh z rôznych oblastí fyziky tak, aby ich mohli prezentovať pred odbornou porotou. Úlohy sú dopredu známe. Na samotnej súťaži družstvo prezentuje niekoľko úloh a oponuje riešenia iných družstiev. Študenti sa tak učia nielen fyzike, ale učia sa i predkladať svoje výsledky a objektívne hodnotiť výsledky iných.
Naša škola sa zúčastňuje TMF od školského roku 1996/97. Odvtedy sme obsadili v celoslovenskom kole súťaže štyrikrát 2. miesto a dvakrát 3. miesto. Hlavne v posledných rokoch pri riešení úloh pomáha viacero študentov. Piati študenti našej školy boli postupne členmi výberu Slovenska v piatich ročníkoch súťaže.
Hoci najkrajšie na súťaži je hľadanie a nachádzanie riešení, pre úspech sú rozhodujúce vedecké diskusie o riešených problémoch. Tie sa uskutočňujú v tzv. fyzbojoch. Fyzboj prebieha medzi tromi družstvami v troch etapách tak, že každé družstvo v jednej etape zaujme jedno z postavení „referent – oponent – recenzent“. Každé družstvo sa vo fyzboji cyklicky vystrieda vo všetkých pozíciách.
Každá etapa fyzboja začína tým, že oponent zadáva úlohu referentovi, ktorý ju prijme alebo odmietne. Pri odmietnutí oponent určí inú úlohu. Družstvo môže v priebehu celej súťaže odmietnuť bez penalizácie tri rôzne úlohy. Odmietanie ďalších úloh znižuje bodové hodnotenie družstva.
Každý člen družstva môže v priebehu jedného fyzboja vystúpiť maximálne dvakrát. Každé družstvo môže referovať alebo oponovať jednu úlohu najviac raz. Niektoré úlohy treba referovať, oponovať a recenzovať v angličtine.
2 Modelovanie fyzikálnych dejov pomocou programu IP-Coach
Modelovanie fyzikálnych dejov napomáha lepšie porozumenie ich podstaty. Pri modelovaní pomocou programu IP-Coach študenti nepotrebujú vedieť programovať. Túto možnosť ilustrujeme na jednej úlohe.
Tvrdohlavý ľad. Vložte kúsok ľadu (napríklad kocku ľadu) do nádoby naplnenej rastlinným olejom. Pozorujte jeho pohyb a kvantitatívne popíšte jeho dynamiku. (Úloha č. 02 z roku 2004)
Rozhodujúcimi silami pôsobiacimi na kocku ľadu v priebehu jej topenia sú tiažová sila Fg, vztlaková sila Fa, povrchová sila Fp pôsobiaca na ľad na hladine a odporová sila Fo. Pretože hustota ľadu je menšia ako hustota oleja, najskôr pláva kocka ľadu na hladine. Ľad sa postupne topí, roztopená voda vďaka povrchovému napätiu ostáva pri ľade, a keďže hustota vody je väčšia ako hustota oleja, voda ťahá ľad nadol. Keď tiaž roztopenej vody prekoná silu povrchového napätia medzi ľadom a vodou, voda odkvapne a ľad zase stúpa k hladine. Situácia je ilustrovaná na obr. 1.
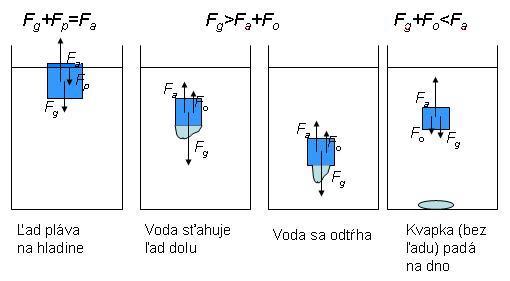
Obr. 1. Jednotlivé fázy pohybu kúska ľadu v oleji
Rýchlosť topenia, a tým aj dynamika pohybu ľadu závisí od množstva tepla, ktoré ľad príjme od oleja. To je funkciou veľkosti povrchu ľadu, teploty oleja a času. Presne zistiť tok tepla v tomto prípade nie je jednoduché, preto sme použili zjednodušenie, že len istá vrstva oleja efektívne odovzdáva teplo ľadu. Tiež sme zanedbali zmenu teploty oleja počas pokusu. Dostali sme tak sústavu rovníc, ktoré umožňujú kvantitatívne popísať pohyb ľadu. Ich riešenie sme urobili numericky s využitím programu IP-Coach. Výpis programu je uvedený nižšie.
| MODEL 'výpočet objemu ľadu vl, hrany kocky ľadu b, a objemu vzniknutej vody vv: vl=ml/rl b=vl^(1/3) vv=mv/rv
'výpočet tepla dq, ktoré prijme ľad za časový interval dti (ľad prijíma teplo od oleja cez svojich 5 stien, lebo dole je kvapka vody s teplotou 0ºC):
S=5*b*b dq=la*S*dT/x*dti
dm=dq/l mv=mv+dm ml=ml-dm m=ml+mv
'výpočet sily pôsobiace na ľad celý ponorený v oleji, a v prípade, keď časť ľadu vyčnieva nad hladinu oleja: F=m*g-ro*g*(vl+vv)-k*b*v if y<b then F=m*g-ro*g*(b*b*y+vv)-k*v*b-k1*h
v=v+a*dti y=y+ v*dti y1=-y*100
a=0 v=0 |
POČIATOČNÉ HODNOTY 'hustota ľadu rl, vody rv a oleja ro, počiatočná hmotnosť ľadu ml a vody mv:
ro=920 'kg/m^3 rv=1000 'kg/m^3 ml=12.44e-3 'kg mv=0 'kg
'koeficient tepelnej vodivosti oleja la, šírka vrstvy oleja x, ktorá priamo odovzdáva teplo ľadu, rozdiel teplôt ľadu a oleja dT, merné skupenské teplo topenia ľadu l:
la=0.5 'J/(m.s.K) dT=20 'C x=4e-3 'm l=334e3 'J/kg 'počiatočná hĺbka ponorenia spodnej steny kocky ľadu y, rýchlosť pohybu ľadu v:
y=0 'm v=0 'm/s
'tiažové zrýchlenie g, konštanta pri sile odporu kocky ľadu proti pohybu k, a sile povrchového napätia oleja k1: k=10 'N.s/m^2 mvmax=5e-4 'kg ymax=0.10 'm dti=0.04 's |
Veľkosti počiatočných hodnôt jednotlivých veličín sme zistili z tabuliek alebo odhadli na základe pozorovaní.
Výsledky tohto modelu sú uvedené na obr. 2. Vidíme sa počas 610 s vytvorí asi 20 kvapiek vody, pričom čas tvorby nasledujúcej kvapky postupne narastá. Vznikajúca kvapka vody ťahá kocku nadol. Po jej odkvapnutí ľad stúpa nahor. Pohyb spočiatku nie je výrazný, lebo kocka ľadu (a tým aj vztlaková sila) je príliš veľká. Spodná stena kocky ľadu najskôr klesne asi 3 cm pod hladinu, no po niekoľkých sekundách ostáva tesne pod hladinou. Keďže sa topí, postupne sa blíži k hladine. Až asi od 250 s začne byť pokles kocky ľadu pri odpadnutí kvapky vody výrazný.
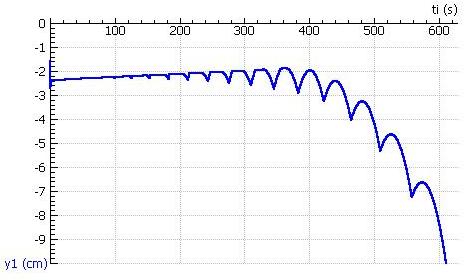
Obr. 2. Závislosť hĺbky ponorenia spodnej hrany ľadu od času získaná modelovaním
Pokus sme urobili s viacerými druhmi oleja a ľadu. Hĺbku ponorenia spodnej steny ľadu v okamihu odkvapnutia vody sme merali s presnosťou ±3 mm pomocu pravítka umiestneného vedľa kadičky s olejom. Čas odkvapnutia sme merali stopkami s presnosťou ±0,2 s. Na obr. 3 sú uvedené naše výsledky pre olej Venusz a ľad z destilovanej vody. Z obr. 3a vidíme, že v súlade s výsledkami modelu sa vytvorilo 19 kvapiek vody, pri ktorých čas tvorenia postupne narastá. Z obr. 3b je zrejmé, že hĺbka ponorenia spodnej steny ľadu v okamihu odtrhnutia kvapky sa najskôr zmenšuje, a potom asi od 250 s narastá. Oba tieto výsledky sa kvalitatívne zhodujú s teoretickým modelom. (Aj keď priblíženie spodnej steny kocky ľadu k hladine je v modeli menšie.)
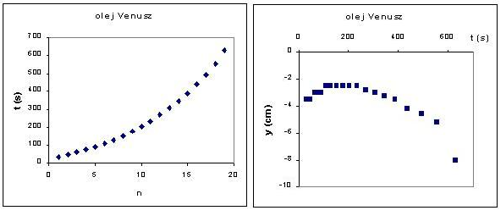
Obr. 3. Výsledky experimentu. a) Závislosť času odkvapnutia kvapky vody od počtu kvapiek. b) Závislosť hĺbky ľadu pod hladinou pri odkvapnutí kvapky od času
3 Realizácia experimentov pomocou programu IP-Coach
Niekedy, napríklad pri meraní veľmi krátkych časov, vysokých frekvencií, rýchlostí nerovnomerných pohybov alebo pri veľkom množstve rutinných meraní, je vhodné merania automatizovať. To sme urobili pri viacerých úlohách, pričom sme použili senzory zvuku, svetla, teploty, polohy a pod. Situáciu tiež ilustrujeme na jednej úlohe.
Vrtiaca sa guľa. Oceľová guľôčka s priemerom 2-3 cm je položená na horizontálnej platni. Vymyslite a zostrojte zariadenie, ktoré umožní roztočiť guľôčku do vysokej uhlovej rýchlosti okolo zvislej osi. Zariadenie nesmie mať žiaden mechanický kontakt s guľôčkou. (Úloha 13/2002)
Na obr. 4 je naznačené ako zariadenie funguje.
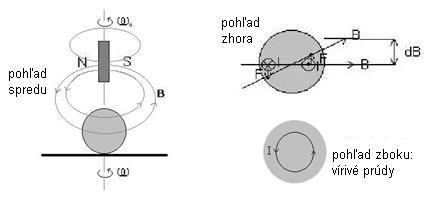
Obr. 4. Pohľad na guľôčku v otáčavom magnetickom poli permanentného magnetu z troch strán
Ak roztočíme permanentný magnet s uhlovou rýchlosťou ω0, v jeho okolí vznikne otáčavé magnetické pole B, ktoré indukuje v guľôčke vírivé prúdy I. Na ne pôsobí magnetické pole silou F, ktorá guľôčku roztáča uhlovou rýchlosťou ω
.Pri odvodení vzťahu sme použili priblíženie jedinej prúdovej slučky tečúcej guľôčkou, homogénneho magnetického poľa v guľôčke a efektívneho ramena pôsobiacej sily. Potom sme pre moment sily τ pri roztáčaní (a pri zanedbaní trenia) dostali:
![]()
V uvedených vzťahoch je J moment zotrvačnosti gule, a index ef označuje efektívnu hodnotu jednotlivých veličín (plochy, prúdovej slučky, ramena sily a elektrického odporu). Odtiaľ sa dá pre uhlovú rýchlosť otáčania odvodiť
![]()
Experimentálne overenie vzťahu pre uhlovú rýchlosť odtáčania guľôčky sme urobili pomocou fotobunky. Princíp merania je zrejmý z obr. 5. Intenzita odrazeného svetla sa pri odraze od bieleho pásika na guľke zmení a túto zmenu sme schopní namerať.
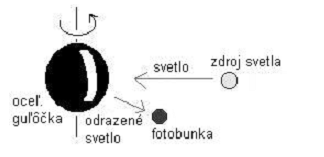
Obr. 5.
Na obr. 6a vidíme záznam signálu fotobunky, ktorý bol získaný programom IP-Coach pri roztáčaní guľôčky. Odtiaľ sme určili periódu kmitov. Po spracovaní meraní aj pre iné okamihy roztáčania guľôčky sme dostali závislosť uhlovej frekvencie od času (obr. 6b). Cez namerané body je preložená krivka zodpovedajúca teoretickej závislosti. Vidíme, že experimentálne výsledky veľmi dobre zodpovedajú teoretickým hodnotám. Podobne sme dokázali analyzovať aj vplyv trenia na pohyb guľôčky.
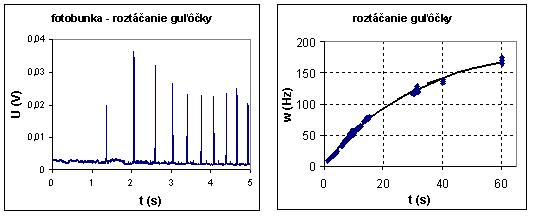
Obr. 6. a) Závislosť napätia fotobunky od času počas prvých 5 s roztáčania guľôčky.
b) Závislosť uhlovej frekvencie od času počas prvej minúty roztáčania.
Literatúra
[1] Organizačný poriadok predmetovej súťaže Turnaj mladých fyzikov. http://www.tmfsr.sk
