Fyzika s Veselou krávou – aneb pokusy s opravdu jednoduchými pomůckami
Leoš Dvořák
Příspěvek popisuje fyzikální pokusy s jednoduchými pomůckami, jejichž základem jsou krabičky od sýra.
Úvod
Jak ukázala už řada příspěvků z Veletrhů nápadů, fyzik či učitel fyziky využije k pokusům cokoli – PET láhve, mince, věci z lékárničky, CD a bůhví co ještě. Jak uvidíme, experimentovat lze i s tak jednoduchou věcí, jako je krabička od sýra.
K řadě pokusů se hodí „káča“ z poloviny kulaté krabičky od tavených sýrů. Osu káči vyrobíme ze zahrocené špejle. Střed dna krabičky předem najdeme třeba zkusmo tak, aby krabička byla vyvážena na hrotu špendlíku. Špejli ke krabičce přilepíme pomocí tavného lepidla. (Viz obr. 1.) Je jen třeba kontrolovat kolmost osy, aby káča příliš neházela. A můžeme začít s pokusy.
Pokusy z mechaniky
Úhlová rychlost – měření pomocí počítače
Na pevné podložce se káča celkem dobře točí. Jak rychle ji vlastně dokážeme v prstech roztočit? Očima nedokážeme otáčení sledovat, natož počítat. Může nám pomoci počítač. K mikrofonnímu vstupu zvukové karty pomocí kablíku připojíme fototranzistor a můžeme snímat změny osvětlení. Na káču stačí nakreslit tužkou značku a při otáčení k těmto místům přiblížit fototranzistor.

Obr. 1 Káča z krabičky od sýra
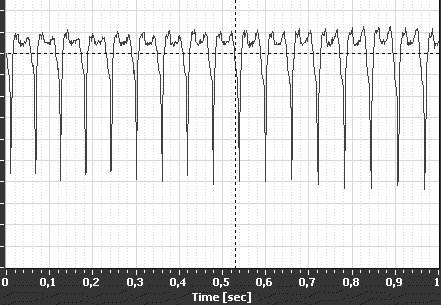
Obr. 2 Signál z rotující káči snímaný fototranzistorem
Signál můžeme nahrávat a vyhodnocovat buď nějakým programem typu Adobe Audition, nebo např. pomocí freewareového programu SoundCard Oscilloscope. Výsledný signál ukazuje obr. 2. Celkový zobrazený čas je 1 s. Již jednoduchým odpočítáním tak zjistíme, že se káča otáčí asi 17-krát za sekundu. Zmíněný software umožňuje dobu mezi impulzy měřit i přesněji. (V daném případě byla frekvence 17,4 Hz.)
Úhlová rychlost – velmi jednoduché měření
Jak si pomoci, nemáte-li po ruce počítač a fototranzistor? K přibližnému změření úhlové rychlosti otáčení stačí položit osu káči vodorovně na hranu stolu. Osa jede po hraně; z dráhy ujeté za 1 s lze lehce spočíst počet otáček za sekundu. (Příslušná úvaha možná pomůže některým žákům názorněji pochopit vztah mezi úhlovou a obvodovou rychlostí.) Aby osa neprokluzovala, můžeme na špejli navléknout kousek gumičky do ventilku zakoupené v prodejně jízdních kol. Celkově je toto měření spíše orientační, ale do asi 20 otáček za sekundu jím úhlovou rychlost přibližně určíme.
Káča jako „skoro smyčka smrti“ (a netradiční měřič tíhového zrychlení)
Vložte do krabičky tvořící naši káču lehký předmět (kousek špejle, matičku či kancelářskou sponku), chyťte krabičku za osu a v prstech ji roztočte. Předmět se samozřejmě posune k okraji. Když teď (za stálého otáčení káči) otočíte osu do vodorovné polohy, předmět zůstane na okraji, i když je zrovna nahoře. Máte vlastně model pouťové atrakce – svislého kola, kde ze sedačky nevypadnete ani v horní úvrati, kdy jste hlavou dolů – resp. téměř model „smyčky smrti“.
Při zpomalování otáček ovšem v jistý okamžik předmět vypadne. (Takový pokus bychom asi na skutečné pouti neradi dělali.) Překvapující je, že se to stane až při dosti nízkých otáčkách, při necelých 2,5 otáčkách za sekundu. Z rovnosti odstředivé síly (řešíme-li situaci v soustavě spojené s krabičkou) a tíhové síly můžeme přibližně vypočítat tíhové zrychlení. (Měříme-li úhlovou rychlost počítačem, jak bylo popsáno výše, lze dosáhnout přesnost téměř 10%.)
Káča jako centrifuga (aneb rotující soustava prakticky)
Naši káču můžeme využít také jako jednoduchou centrifugu. Je zajímavé uvědomit si, že i při relativně nízkých otáčkách může zrychlení na obvodu dosáhnout značných hodnot. Už při roztočení káči v prstech (při výše zmíněných 17 otáčkách za sekundu) činí úhlová rychlost ω přes 100 s-1 a zrychlení u obvodu (r = 5 cm) je tedy více než 500 m/s2, tedy, vyjádřeno v násobcích tíhového zrychlení, přes 50 g!
Vyšších hodnot úhlové rychlosti dosáhneme, roztočíme-li káču vrtačkou nebo pomocí malého elektrického motorku. Malá vrtačka pro modeláře (či na vrtání plošných spojů, lze ji koupit v prodejnách s elektronickými součástkami) má přes 6 tisíc otáček za minutu. To znamená 100 otáček za sekundu, tedy úhlovou rychlost přes 600 s-1. Vypočtěte s vašimi žáky zrychlení na obvodu krabičky! Suchý vzoreček r·ω2 dostane „štávu“ a dá pro mnohé asi překvapující výsledek: téměř 20000 m/s2, tedy téměř 2 tisíce g! Každý gram tedy tlačí na obvod krabičky silou, jakou normálně tlačí na podložku dvoukilové závaží.
Skutečnost, že na tělesa v rotující krabičce opravdu působí velká odstředivá síla, můžeme demonstrovat, vložíme-li do krabičky do dvou protilehlých míst (aby centrifuga zůstala vyvážená) dva malé kousky taveného sýra (kostičky o hraně asi 1 cm). Roztáčení centrifugy v prstech nestačí. Ovšem už při asi 40 otáčkách za sekundu se sýr „rozmázne“ do docela tenké vrstvy. Doporučuji přitom vnitřek krabičky v místě, kde bude sýr, vylepit izolepou či podobnou páskou (aby šel sýr zase sundat) a naši centrifugu zavřít víčkem (jinak sýr radostně odlétá všemi směry). Druhý konec osičky přidržujte v prstech, aby se celá centrifuga nerozvibrovala do stran.
Upozornění: Do otevřené (a raději ani do zavřené) centrifugy poháněné motorkem či vrtačkou nedávejte žádné tvrdší předměty (ani ty sponky, matičky apod.)! Opět je to příležitost pro faktickou fyzikální diskusi s žáky: Při 100 otáčkách za sekundu je obvodová rychlost přes 30 m/s, tedy přes 100 km/h. A kdo by chtěl dostat matičkou letící takovou rychlostí třeba do čela, o očích nemluvě… Obecně dejte pozor, aby z vaší káči nemohlo nic odlétnout (vyplatí se slepit izolepou konce proužku tvořícího plášť krabičky). A raději se nepouštějte do vyšších úhlových rychlostí, i když jich některé malé vrtačky dosáhnou. Při 18 tisíc otáčkách za minutu by bylo zrychlení na obvodu krabičky přes 170 tisíc m/s2 a obvodová rychlost přes 300 km/h. Může být sice zajímavé argumentovat, že desetigramový kousek sýra by pak tlačil na obvod stejnou silou, jako kdyby nám šlápl na nohu urostlý zápasník sumo, ale riziko zranění za to nestojí.
Trocha kmitání
Torzní kyvadlo
Z naší káči můžeme lehce udělat torzní kyvadlo. Stačí na horní konec špejle tvořící osu navléci gumičku z ventilku. Druhý konec gumičky držíme v prstech. Roztočíme-li káču, gumička se zkrucuje (krásný příklad torzní deformace), brzdí otáčení káči a pak ji roztáčí zpátky. Při délce gumičky 8 cm a běžné krabičce od sýrů byla perioda kmitů asi 2,9 s.
Měření momentu setrvačnosti
Předchozí pokus můžeme využít i k měření momentu setrvačnosti krabičky J0. Stačí dát do krabičky vhodné přívažky (jejichž moment setrvačnosti JP budeme znát), změřit periodu torzních kmitů T bez přívažků a periodu T1 s přívažky a ze vztahů pro periody kmitů vypočíst J0 = JP/((T1/T)2-1).
Nemáme-li po ruce přívažky známé hmotnosti, mohou nám pomoci dílky sýra v krabičce. Dle údaje na krabičce má 8 dílků 140 g. Jeden dílek má tedy m = 17,5 g. Protože se dílek rozšiřuje od středu ke kraji, platí pro jeho moment setrvačnosti stejný vztah jako v případě válce, tj. ½·m·r2. Konkrétní měření a výpočet daly pro moment krabičky (resp. její spodní poloviny, včetně osy) hodnotu přibližně J0 = 2·10-5 kg·m2.
Rezonance
Pomocí popsaného torzního kyvadla můžeme demonstrovat i rezonanci. Malé pootáčení horního konce gumičky v prstech vede při vhodné frekvenci k velmi výrazným torzním kmitům krabičky. Rychlé nebo pomalé pootáčení krabičku téměř nerozkmitá.
Něco málo z akustiky
Savartova a Seebeckova siréna – a jedna navíc
Vystřihneme-li v plášti krabičky pravidelné zářezy, funguje po roztočení krabička jako (ne moc hlasitá) siréna. Krabičku opět roztáčíme vrtačkou či motorkem. Dotýkáme-li se zářezů proužkem papíru, jde o Savartovu sirénu, pokud na ně foukáme třeba brčkem, jde o Seebeckovu sirénu.
Další, trochu netradiční možností, je snímat fototranzistorem světlo přerušované „zuby“ na obvodu krabičky. Počítačem můžeme tento signál analyzovat (a podívat se třeba na jeho frekvenční spektrum), ale také zesílit a pak reprodukovat.
Jeden pokus z optiky
Válcové zrcadlo
Proužek lesklé fólie z obalu na květiny, vložený podél vnitřní stěny krabičky, funguje jako válcové zrcadlo. Chod paprsků nejlépe vidíme na přímém slunečním světle (viz obr. 3 a 4).

Obr. 3 Široký svazek paprsků ukáže i vady zobrazení válcovým zrcadlem

Obr. 4 Úzký svazek se zobrazí do ohniska
A dokonce něco směrem k astronomii
Sluneční hodiny
Je-li špejle tvořící osu krabičky rovnoběžná se zemskou osou, může naše krabička fungovat jako sluneční hodiny. Stačí ji „opásat“ proužkem papíru, na němž vyznačíme hodiny (viz obrázek). Díky vhodné velikosti krabičky odpovídá na obvodu jedné hodině délka 1,5 cm. (Je vhodné to zkontrolovat, případně pásek papíru trochu „vypodložit“.) Jak dlouhý kousek špejle nechat pod krabičkou přečnívat, aby osa měla správný sklon, může být úlohou pro žáky.

Trocha teorie aneb srovnáváme velikosti
Pro názornost je možná zajímavé udělat si představu o velikostech velmi velkých a velmi malých věcí. A proč ne srovnáním s naší krabičkou?
Stomiliónkrát zvětšená krabička by měla rozměry Země. (Nepřesnost je zhruba 20%.)
Miliardkrát zmenšená krabička by měla rozměry atomu. (Dokonce bychom tak dostali Bohrův poloměr s přesností na 5%.)
A ještě jedno srovnání: krabička sýra jako dráha Země kolem Slunce. (Měřítko je 1 : 2,7·1012). V tomto modelu by Slunce mělo průměr 0,5 mm, Země asi 5 μm,
oběžná dráha Jupitera by měla průměr necelých 60 cm, oběžná dráha Neptuna 3,3 m, takže se tenhle model právě vejde do třídy...
Na konec trochu „pyramidologie“ ☺
Mnozí se pokoušejí vyčíst tajemství vesmíru z rozměrů Velké (Cheopsovy) pyramidy v Gíze. Proč však obtěžovat pyramidu? Zkusme užít naši krabičku od Veselé krávy! Žasněte, co vše dostaneme:
Poměr průměru krabičky (11 cm) a její výšky (2 cm) umocněný na čtvrtou krát 2 dá asi 1830 – tj. skoro poměr hmotnosti protonu a elektronu (1836,152663). Když za přesnější hodnotu průměru krabičky vezmeme 11,111111cm a za přesnější hodnotu výšky 2,018542011 cm, vyjde to úplně přesně! Konec konců „pyramidologové“ si míry občas také trochu přizpůsobují…
Přibereme-li ke krabičce i pyramidu, je výpočet této konstanty ještě jednodušší. Výška Velké pyramidy (146,7 m) dělená výškou krabičky (2 cm) po vydělení 4 dává 1833,75. Pokud krabičku trochu sešlápneme, jsme opět na přesné hodnotě. :-)
Podobně můžeme dostat i hodnoty dalších fyzikálních konstant. Ale i matematických: úhlopříčka základny Cheopsovy pyramidy (232,4·√2 m) dělená průměrem krabičky (spíš vnitřním: 11,025423 cm) dá po umocnění na 1/8 hodnotu 2,718281..., tedy e.
Přidejte trochu záhadný výraz, zamumlejte k těmto výpočtům něco tajemného – a nebýt v tom ta krabička od sýra, snad by vás někdo začal brát i vážně... Až na vás vaši žáci přijdou s tím, co vše se dá vyčíst z rozměrů pyramid, můžete jim předvést, že leccos nám odhalí i Veselá kráva. Snad je to přivede k poněkud racionálnějšímu a kritičtějšímu pohledu na věc.
Ale ještě bychom neměli zapomenout na jeden naprosto nevyvratitelný „trhák“.
Obvod krabičky vydělený jejím průměrem dá 3,1415926… – opravdu, je to π!
Závěr
A to je vše? Zdaleka ne! Jen rozsah příspěvku nedovoluje popsat všechny nápady. Vždyť jsme se třeba vůbec nedotkli elektřiny a magnetismu. Takže možná někdy
nashledanou u Fyziky s Veselou krávou II.
A pokud vám tento příspěvek bude alespoň v něčem inspirací, splnil svůj účel.
