Světelné hrátky

Stanislav Gottwald

Příspěvek se zabývá způsoby, kterými je možno získat polarizované světlo, včetně jejich objasnění na konkrétních příkladech a experimentech, jež si mohou studenti sami provést. Poslední část se zmiňuje o tom, jak si doma připravit modrou oblohu v akváriu a duhu z „věštecké“ koule.

Optika v učivu fyziky

Oblast fyziky, která se zabývá světlem, je studenty zařazována mezi nejoblíbenější učivo. Asi proto, že existuje celá řada pokusů, které probírané jevy jednoduše demonstrují, a navíc s řadou jevů se studenti ve svém okolí běžně setkávají. Jde jen o to naučit se tyto jevy vnímat a správně pochopit. Značná část studentů se mi svěřila, že teprve po hodinách fyziky si začala více všímat optických jevů kolem sebe (např. optických jevů v atmosféře, duhových obrazců kolem lamp pouličního osvětlení, interferenčních jevů apod.). Může se proto také stát, že si všimnou čehosi, co jsem i já přehlédl. O to zajímavější je pak pro obě strany takový jev společně podrobit důkladnému zkoumání.

Mezi obzvláště zajímavé (i když ne vždy triviální) jevy, se kterými se studenti setkávají, patří polarizace světla a optické jevy v atmosféře. Některé z nich jsou na první pohled nenápadné, málo výrazné - o to více nás jejich existence překvapí. Řada je navíc atraktivní svou barevností. Optické jevy v atmosféře jsou většinou dobře pozorovatelné a známé, a proto studenti sami kladou otázky po příčinách jejich vzniku a jsou tak k jejich studiu dobře motivováni. K ilustraci těchto jevů dnes již najdeme celou řadu fotografií (případně apletů a animací) na internetu. Pochopitelně si je můžeme také pořídit sami svým fotoaparátem (do jejich sběru je vhodné zapojit i studenty). Poměrně jednoduchá a rychlá je manipulace se soupravami firmy Prague Precision, s.r.o. (Pod Útesy 8, Praha 5), které umožňují řadu jevů demonstrovat s využitím zpětného projektoru nebo i frontálně (souprava na interferenci světla). Soupravy jsou navíc doplněny poměrně obsáhlými doprovodnými texty. Jejich cena se však pohybuje kolem osmi tisíc. Já sám je využívám v kombinaci s vlastnoručně shromážděnými (resp. zpravidla nasbíranými) pomůckami (polarizační filtry a displeje z kalkulaček, mobilních telefonů, polarizační brýle apod.)

Polarizace světla

Protože světlo je příčné (elektromagnetické) vlnění, setkáváme se u něj s jevem polarizace. Přírodní zdroje vyzařují světlo, které kmitá v různých směrech kolmých na směr šíření, přičemž jeho kmitová rovina se neustále chaoticky mění. To je dáno mechanizmem vzniku světla v elektronových obalech. Protože studenti vyšších ročníků SŠ tento mechanizmus v době zkoumání polarizace dobře znají, jsou schopni si vytvořit poměrně vhodný a názorný model, který jim pomůže k objasnění řady jevů. Polarizátory, tedy „zařízení“, která jsou schopna vybrat jen jednu kmitovou rovinu, pracují zpravidla na základě jednoho z následujících mechanizmů:

Metody získávání polarizovaného světla

Polarizace selektivní absorpcí (dichroizmus)

Některé látky procházející světlo štěpí na dvě složky, které kmitají v navzájem kolmých rovinách, přičemž jedna složka se v nich postupně tlumí a druhá prochází téměř beze změny. Vystupující světlo je pak lineárně polarizované. Tyto polarizátory se nazývají polarizační filtry (polaroidy, dichroické polarizátory) a nejčastěji se používají při analýze polarizace světla a demonstracích průchodu světla dvojicí polarizátorů. Studenti je dobře znají především z polarizačních brýlí. Zde je vhodné připomenout využití těchto filtrů ve spojení s kapalnými krystaly. Změnu propustnosti kapalných krystalů účinkem elektrického pole můžeme pozorovat v propuštěném světle (dataprojektor) nebo světle odraženém (mobilní telefon, kalkulačka…).

Polarizace odrazem a průchodem

V odraženém světle zpravidla kmitá vektor intenzity elektrického pole rovnoběžně s odrazivou plochou (tj. kolmo k rovině dopadu). Asi nepřekvapí, že ve světle procházejícím (lomený paprsek) tato složka naopak částečně chybí. Odražené světlo je úplně polarizované jen při tzv. Brewsterově (neboli polarizačním) úhlu dopadu α_B. Dopadá-li světlo ze vzduchu na rozhraní s prostředím o indexu lomu n platí

Stanislav Gottwald : Světelné hrátky - image002.jpg

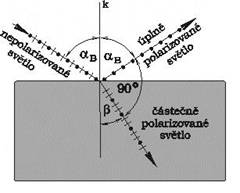
Při úhlu dopadu αB svírá odražený a lomený paprsek úhel 90º, lomený paprsek však úplně polarizovaný není, jeho polarizace se zvětší vícenásobným lomem.

Stanislav Gottwald : Světelné hrátky - image006.jpg

Díváme-li se na odrazivou plochu (případně obraz na této ploše vznikající odrazem) přes polarizační filtr, zjišťujeme, že se intenzita odraženého světla mění v závislosti na orientaci (pootočení) filtru i na směru pozorování. Víme-li, jaký kmitový směr filtr propouští, můžeme určit směr polarizace paprsku odraženého.

Stanislav Gottwald : Světelné hrátky - image008.jpg

Polarizace dvojlomem

U některých (anizotropních) látek se dopadající světlo rozštěpí na dva paprsky, které jsou lineárně polarizované v navzájem kolmých rovinách - na paprsek řádný (řídí se Snellovým zákonem lomu) a paprsek mimořádný. Oba paprsky se šíří obecně různou rychlostí a různým směrem (samozřejmě nedopadá-li světlo ve směru tzv. optické osy). Oddělíme-li oba paprsky od sebe (zpravidla necháme pohltit paprsek řádný), dostáváme polarizované světlo (poměrně drahé krystalové polarizátory, např. Nikolův hranol). Podíváme-li se přes takovou látku, uvidíme dva obrazy. Pokud si dáme před oko polarizační filtr a otáčíme-li jím, budou střídavě obrazy mizet.

Umělý dvojlom

Optická anizotropie látek se dá „vyprovokovat“ vnějšími vlivy – např. magnetickým a elektrickým polem, mechanickým napětím. Některé (amorfní) látky se stanou dvojlomnými, vzniknou-li v nich vnitřní napětí např. při tuhnutí a chladnutí, vnějším namáháním. Vložíme-li takovou látku (např. model z plexiskla) mezi dva polarizační filtry, pozorovaný obrazec poskytne informace o rozložení mechanického napětí. Nemusíme mít žádný složitý model, stačí obyčejné průhledné pravítko. Vložíme-li pravítko mezi dva polarizační filtry umístěné na zpětném projektoru, můžeme s celou třídou pozorovat nádherné barevné obrazce. V místě, kde jsou barevné čáry nejhustší, bylo pravítko vystaveno velkému mechanickému namáhání (v místě vlisů apod.)

Vznik barevných efektů

Dopadá-li na destičku z dvojlomného materiálu polarizované světlo, obecně se štěpí na dva paprsky, které se šíří různou rychlostí (tj. látka má různý index lomu: n_e pro paprsek mimořádný a n_o pro paprsek řádný). Mezi paprsky vzniká určitý dráhový rozdíl, který je přímo úměrný tloušťce d destičky a rozdílu obou indexů lomu. Oba paprsky se po průchodu skládají, přitom výsledek závisí na fázovém rozdílu , kde λ je vlnová délka dopadajícího světla. Bude-li fázový rozdíl mezi paprsky např. 2π, složené světlo bude polarizováno ve stejné rovině jako světlo dopadající, v případě fázového rozdílu π v rovině kolmé k rovině původního světla. Díváme-li se tedy na destičku přes další polarizační filtr, světlo prochází, či neprochází v závislosti na úhlu jeho pootočení. V případě, že je fázový rozdíl jiný než jsou obě výše uvedené extrémní situace, vznikne světlo kruhově polarizované, které filtrem projde částečně.

Pokud experiment provádíme v bílém světle, je pozorovaný jev výslednicí různých propustností destičky pro jednotlivé vlnové délky (barvy). Destička se pak chová jako filtr, který některé barevné pásy pohltí, jiné propustí. Závislost propustnosti na indexu lomu (který je ovlivněn mechanickým napětím v látce) je zřejmá z pokusu s pravítkem (které je umístěno mezi polarizačními filtry). Závislost na tloušťce destičky je pěkně vidět na průhledné lepicí pásce, která je dvojlomná. Nalepováním pásek přes sebe vznikne několik vrstev, které jsou pak různě barevné. Vzájemným otáčením obou filtrů, můžeme ukázat i závislost na úhlu natočení.

Pěkné barevné (i když ne tak výrazné) efekty můžeme pozorovat na průhledných umělohmotných materiálech za slunečného dne (nejspíše si studenti jevu všimnou na krabičce od CD). Ve třídě pak můžeme diskutovat, proč pozorujeme tyto efekty bez přítomnosti nějakého speciálního zdroje polarizovaného světla. Při tom je vhodné zopakovat, jak si polarizované světlo můžeme „připravit“. Jev je výraznější, když např. výše zmíněné CD pozorujeme polarizačním sklem, tím odfiltrujeme odražené polarizované paprsky. Výraznost barevných pásů závisí na orientaci filtru i na úhlu pod kterým tyto obrazce pozorujeme.

Rozptyl světla, aneb proč je obloha modrá

Často kladenou otázkou studentů je: „Proč je obloha modrá?“ Příčinou je naše atmosféra. Kdyby tady nebyla, připadali bychom si ve dne jako na jevišti osvětleném slunečním reflektorem. Za to, že světlo slunce proniká do našich domů a všech zákoutí (i tzv. za roh), může rozptyl světla v atmosféře. Při dopadu světla na nějaké malé tělísko se vyvolávají kmity elektronů, které jako malé anténky vyzařují do okolí „druhotné“ světlo téměř všemi směry. Existuje mnoho druhů rozptylu, které se liší podle velikostí rozptylujících částic. Zde se jedná o tzv. Rayleighův rozptyl. Je nazván podle významného anglického fyzika, jenž formuloval zákon, podle kterého závisí intenzita rozptýleného světla nepřímo úměrně na čtvrté mocnině jeho vlnové délky. Jde o rozptyl na chaotických fluktuacích hustoty v atmosféře (to zase matematicky vysvětlil Einstein). Ze zákona je patrné, že světlo o velké vlnové délce (červené) se rozptyluje méně než světlo o malé vlnové délce (modré). Ze slunečního kotouče je tak odfiltrováno modré a fialové světlo, které zabarví okolní oblohu. (Nebe není fialové ale modré proto, že fialového světla je ve slunečním záření méně než modrého a navíc je naše oko na modrou barvu citlivější.)

Naplníme-li akvárium vodou a přidáme-li několik kapek mléka, pozorujeme při osvětlení úzkým svazkem z intenzivního zdroje světla (např. diaprojektoru), že je akvárium zabarveno domodra; při čelním pohledu je zdroj červený.

Rozptýlené světlo je navíc také polarizované. To je možné ověřit polarizačními brýlemi přímo při pohledu na oblohu – při otáčení brýlí se mění intenzita svitu některých částí oblohy. Hmyz tyto různé stavy polarizace dokáže rozlišovat, proto zřejmě tohoto jevu využívá k navigaci.

Duha

Asi nejznámějším a zároveň nejobdivuhodnějším a poměrně komplikovaným optickým úkazem, kterým nás příroda obdařila, je duha. Každý ji viděl, ale ne každý si uvědomuje obrovskou šíři jevů, které zahrnuje. Vysvětlit do všech podrobností její fyzikální podstatu je opravdu tvrdý oříšek. Uplatňuje se zde disperze světla, jeho interference i polarizace. Není bez zajímavosti se zabývat i historií jejího zkoumání. V souvislosti s tím bychom neměli pozapomenout na osobu významného českého učence Jana Marka Marci. Ačkoli bývá prvenství při objasnění základních vlastností duhy tradičně připisováno I. Newtonovi, již několik let před ním vydal o duze spis právě Jan Marci.

Simulovat vznik duhy na jedné kapce je možné s využitím kulové baňky s vodou, nebo se skleněnou „věšteckou“ koulí. Vhodným zdrojem světla je např. diaprojektor s jednou čočkou a vloženou úzkou vodorovnou štěrbinou. Duhu pak můžeme pozorovat na stínítku nad spojnicí koule-projektor. Dopadá-li svazek paprsků na spodní část koule, pozorujeme tzv. primární (hlavní) duhu, při dopadu paprsků na vrchní část vzniká méně výrazná sekundární (vedlejší) duha, která leží vzhledem ke kouli níž. Zatímco oblouk hlavní duhy je výrazný a dobře pozorovatelný prakticky ze všech míst učebny, vedlejší duha je slabá (vzniká při dvou odrazech uvnitř naší improvizované kapky), a proto se studenti musí přesunout blíž.

Na naší jednokapkové duze můžeme pozorovat a vysvětlit tvar, pořadí barev a různou intenzitu primárního i sekundárního oblouku. Na internetu je řada obrázků a apletů (viz např. [4], [6] ), kterými je vhodné zkoumání duhy doplnit a názorně ukázat, proč je duha vidět pod určitým úhlem (hlavní duha pod úhlem 42° a vedlejší pod úhlem 53°), nebo jak se její vzhled mění s velikostí kapek. Ve vyšších ročnících gymnázií (například na semináři z fyziky nebo matematiky) je možné zjistit průběh tzv. duhové funkce (maximum a minimum má právě pro tyto úhly!) a lépe tak objasnit, proč je obloha mezi oběma oblouky tmavší než je tomu v jejich okolí.

Protože paprsek prochází v kapce několika odrazy a lomy, dochází i k jeho značné polarizaci. Spočítáme-li si jaké paprsky tvoří duhu, zjistíme, že dopadají na zadní stěnu kapky pod úhlem, který je shodou okolností blízký úhlu Brewsterovu. Máme-li při vzniku duhy na obloze po ruce polarizační filtr, polarizaci duhy si sami snadno ověříme.